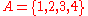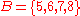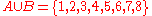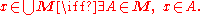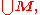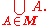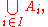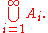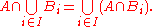Home Discussion Topics Dictionary Almanac

Signup Login

Union (set theory)

Discussion

Ask a question about 'Union (set theory)'

Start a new discussion about 'Union (set theory)'

Answer questions from other users

Full Discussion Forum

Encyclopedia

In set theory

Set theory

Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...

, the union (denoted as ∪) of a collection of sets is the set of all distinct elements in the collection. The union of a collection of sets

gives a set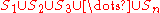

.

Definition

The union of two sets A and B is the collection of points which are in A or in B (or in both):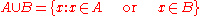

A simple example:

Other more complex operations can be done including the union, if the set is for example defined by a property rather than a finite or assumed infinite enumeration of elements. As an example, a set could be defined by a property or algebraic equation, which is referred to as a solution set when resolved. An example of a property used in a union would be the following:

A = {x is an even number, x > 1}

B = {x is an odd number, x > 1}

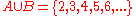
If we are then to refer to a single element by the variable "x", then we can say that x is a member of the union if it is an element present in set A or in set B, or both.

Sets cannot have duplicate elements, so the union of the sets {1, 2, 3} and {2, 3, 4} is {1, 2, 3, 4}. Multiple occurrences of identical elements have no effect on the cardinality of a set or its contents. The number 9 is not contained in the union of the set of prime number

Prime number

A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...

s {2, 3, 5, 7, 11, …} and the set of even numbers {2, 4, 6, 8, 10, …}, because 9 is neither prime nor even.

Algebraic properties

Binary union is an associative operation; that is,

A ∪ (B ∪ C) = (A ∪ B) ∪ C.

The operations can be performed in any order, and the parentheses may be omitted without ambiguity (i.e. either of the above can be expressed equivalently as A ∪ B ∪ C).
Similarly, union is commutative, so the sets can be written in any order.
The empty set

Empty set

In mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...

is an identity element

Identity element

In mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...

for the operation of union.
That is, A ∪ {} = A, for any set A.
In terms of the definitions, these facts follow from analogous facts about logical disjunction

Logical disjunction

In logic and mathematics, a two-place logical connective or, is a logical disjunction, also known as inclusive disjunction or alternation, that results in true whenever one or more of its operands are true. E.g. in this context, "A or B" is true if A is true, or if B is true, or if both A and B are...

.

Together with intersection

Intersection (set theory)

In mathematics, the intersection of two sets A and B is the set that contains all elements of A that also belong to B , but no other elements....

and complement

Complement (set theory)

In set theory, a complement of a set A refers to things not in , A. The relative complement of A with respect to a set B, is the set of elements in B but not in A...

, union makes any power set into a Boolean algebra.
For example, union and intersection distribute over each other, and all three operations are combined in De Morgan's laws.
Replacing union with symmetric difference

Symmetric difference

In mathematics, the symmetric difference of two sets is the set of elements which are in either of the sets and not in their intersection. The symmetric difference of the sets A and B is commonly denoted by A\,\Delta\,B\,orA \ominus B....

gives a Boolean ring

Boolean ring

In mathematics, a Boolean ring R is a ring for which x2 = x for all x in R; that is, R consists only of idempotent elements....

instead of a Boolean algebra.

Finite unions

More generally, one can take the union of several sets at once.
The union of A, B, and C, for example, contains all elements of A, all elements of B, and all elements of C, and nothing else.
Formally, x is an element of A ∪ B ∪ C if and only if x is in A, B, or C.

Union is an associative operation, it doesn't matter in what order unions are taken. In mathematics a finite union means any union carried out on a finite number of sets: it doesn't imply that the union set is a finite set.

Arbitrary unions

The most general notion is the union of an arbitrary collection of sets.
If M is a set whose elements are themselves sets, then x is an element of the union of M if and only if

If and only if

In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....

for at least one

Existential quantification

In predicate logic, an existential quantification is the predication of a property or relation to at least one member of the domain. It is denoted by the logical operator symbol ∃ , which is called the existential quantifier...

element A of M, x is an element of A.
In symbols:

That this union of M is a set no matter how large a set M itself might be, is the content of the axiom of union

Axiom of union

In axiomatic set theory and the branches of logic, mathematics, and computer science that use it, the axiom of union is one of the axioms of Zermelo-Fraenkel set theory, stating that, for any set x there is a set y whose elements are precisely the elements of the elements of x...

in axiomatic set theory.

This idea subsumes the above paragraphs, in that for example, A ∪ B ∪ C is the union of the collection {A,B,C}.
Also, if M is the empty collection, then the union of M is the empty set.
The analogy between finite unions and logical disjunction extends to one between arbitrary unions and existential quantification

Existential quantification

In predicate logic, an existential quantification is the predication of a property or relation to at least one member of the domain. It is denoted by the logical operator symbol ∃ , which is called the existential quantifier...

.

The notation for the general concept can vary considerably, such as the following:

which refers to the union of the collection {A_i : i is in I}.
Here I is an index set

Index set

In mathematics, the elements of a set A may be indexed or labeled by means of a set J that is on that account called an index set...

, and A_i is a set for every i in I.
In the case that the index set I is the set of natural number

Natural number

In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...

s, the notation is analogous to that of infinite series

Series (mathematics)

A series is the sum of the terms of a sequence. Finite sequences and series have defined first and last terms, whereas infinite sequences and series continue indefinitely....

:

When formatting is difficult, this can also be written "A₁ ∪ A₂ ∪ A₃ ∪ ···".
(This last example, a union of countably many sets, is very common in analysis; for an example see the article on σ-algebras.)
Whenever the symbol "∪" is placed before other symbols instead of between them, it is of a larger size.

Intersection distributes over infinitary union, in the sense that

Infinitary union can be combined with infinitary intersection to get the law

.

External links