
Codimension
Encyclopedia
In mathematics
, codimension is a basic geometric idea that applies to subspaces in vector space
s, and also to submanifold
s in manifold
s, and suitable subset
s of algebraic varieties.
The dual concept is relative dimension
.
If W is a linear subspace
of a finite-dimensional vector space
V, then the codimension of W in V is the difference between the dimensions: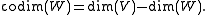
It is the complement of the dimension of W, in that, with the dimension of W, it adds up to the dimension of the ambient space V: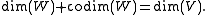
Similarly, if N is a submanifold or subvariety in M, then the codimension of N in M is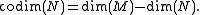
Just as the dimension of a submanifold is the dimension of the tangent bundle
(the number of dimensions that you can move on the submanifold), the codimension is the dimension of the normal bundle
(the number of dimensions you can move off the submanifold).
More generally, if W is a linear subspace
of a (possibly infinite dimensional) vector space
V then the codimension of W in V is the dimension (possibly infinite) of the quotient space
V/W, which is more abstractly known as the cokernel
of the inclusion. For finite-dimensional vector spaces, this agrees with the previous definition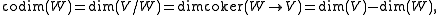
and is dual to the relative dimension as the dimension of the kernel
.
Finite-codimensional subspaces of infinite-dimensional spaces are often useful in the study of topological vector space
s.
: if W1 has codimension k1, and W2 has codimension k2, then if U is their intersection with codimension j we have
In fact j may take any integer
value in this range. This statement is more perspicuous than the translation in terms of dimensions, because the RHS
is just the sum of the codimensions. In words
This statement is called dimension counting, particularly in intersection theory.
, it is quite evident why dimensions add. The subspaces can be defined by the vanishing of a certain number of linear functional
s, which if we take to be linearly independent, their number is the codimension. Therefore we see that U is defined by taking the union
of the sets of linear functionals defining the Wi. That union may introduce some degree of linear dependence: the possible values of j express that dependence, with the RHS sum being the case where there is no dependence. This definition of codimension in terms of the number of functions needed to cut out a subspace extends to situations in which both the ambient space and subspace are infinite dimensional.
In other language, which is basic for any kind of intersection theory
, we are taking the union of a certain number of constraint
s. We have two phenomena to look out for:
The first of these is often expressed as the principle of counting constraints
: if we have a number N of parameter
s to adjust (i.e. we have N degrees of freedom
), and a constraint means we have to 'consume' a parameter to satisfy it, then the codimension of the solution set is at most the number of constraints. We do not expect to be able to find a solution if the predicted codimension, i.e. the number of independent constraints, exceeds N (in the linear algebra case, there is always a trivial, null vector
solution, which is therefore discounted).
The second is a matter of geometry, on the model of parallel lines
; it is something that can be discussed for linear problems by methods of linear algebra, and for non-linear problems in projective space
, over the complex number
field.
: on a manifold, codimension 1 is the dimension of topological disconnection by a submanifold, while codimension 2 is the dimension of ramification
and knot theory
. In fact, the theory of high dimensional manifolds, which starts in dimension 5 and above, can alternatively be said to start in codimension 3, because higher codimensions avoid the phenomenon of knots. Since surgery theory
requires working up to the middle dimension, once one is in dimension 5, the middle dimension has codimension greater than 2, and hence one avoids knots.
This quip is not vacuous: the study of embeddings in codimension 2 is knot theory, and difficult, while the study of embeddings in codimension 3 or more is amenable to the tools of high dimensional geometric topology, and hence considerably easier.
To state the main topological codimension theorems more formally: in codimension 0, immersions may or may not exist; in codimension 1, immersions always exist but embedding
s may or may not exist; in codimension 2, embedding
s exist but may or may not be isotopic; in codimension 3 all embeddings are isotopic.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, codimension is a basic geometric idea that applies to subspaces in vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
s, and also to submanifold
Submanifold
In mathematics, a submanifold of a manifold M is a subset S which itself has the structure of a manifold, and for which the inclusion map S → M satisfies certain properties. There are different types of submanifolds depending on exactly which properties are required...
s in manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
s, and suitable subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
s of algebraic varieties.
The dual concept is relative dimension
Relative dimension
In mathematics, specifically linear algebra and geometry, relative dimension is the dual notion to codimension.In linear algebra, given a quotient map V \to Q, the difference dim V − dim Q is the relative dimension; this equals the dimension of the kernel.In fiber bundles, the relative dimension of...
.
Definition
Codimension is a relative concept: it is only defined for one object inside another. There is no “codimension of a vector space (in isolation)”, only the codimension of a vector subspace.If W is a linear subspace
Linear subspace
The concept of a linear subspace is important in linear algebra and related fields of mathematics.A linear subspace is usually called simply a subspace when the context serves to distinguish it from other kinds of subspaces....
of a finite-dimensional vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
V, then the codimension of W in V is the difference between the dimensions:
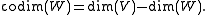
It is the complement of the dimension of W, in that, with the dimension of W, it adds up to the dimension of the ambient space V:
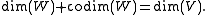
Similarly, if N is a submanifold or subvariety in M, then the codimension of N in M is
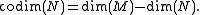
Just as the dimension of a submanifold is the dimension of the tangent bundle
Tangent bundle
In differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...
(the number of dimensions that you can move on the submanifold), the codimension is the dimension of the normal bundle
Normal bundle
In differential geometry, a field of mathematics, a normal bundle is a particular kind of vector bundle, complementary to the tangent bundle, and coming from an embedding .-Riemannian manifold:...
(the number of dimensions you can move off the submanifold).
More generally, if W is a linear subspace
Linear subspace
The concept of a linear subspace is important in linear algebra and related fields of mathematics.A linear subspace is usually called simply a subspace when the context serves to distinguish it from other kinds of subspaces....
of a (possibly infinite dimensional) vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
V then the codimension of W in V is the dimension (possibly infinite) of the quotient space
Quotient space (linear algebra)
In linear algebra, the quotient of a vector space V by a subspace N is a vector space obtained by "collapsing" N to zero. The space obtained is called a quotient space and is denoted V/N ....
V/W, which is more abstractly known as the cokernel
Cokernel
In mathematics, the cokernel of a linear mapping of vector spaces f : X → Y is the quotient space Y/im of the codomain of f by the image of f....
of the inclusion. For finite-dimensional vector spaces, this agrees with the previous definition
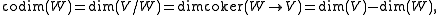
and is dual to the relative dimension as the dimension of the kernel
Kernel (algebra)
In the various branches of mathematics that fall under the heading of abstract algebra, the kernel of a homomorphism measures the degree to which the homomorphism fails to be injective. An important special case is the kernel of a matrix, also called the null space.The definition of kernel takes...
.
Finite-codimensional subspaces of infinite-dimensional spaces are often useful in the study of topological vector space
Topological vector space
In mathematics, a topological vector space is one of the basic structures investigated in functional analysis...
s.
Additivity of codimension and dimension counting
The fundamental property of codimension lies in its relation to intersectionIntersection (set theory)
In mathematics, the intersection of two sets A and B is the set that contains all elements of A that also belong to B , but no other elements....
: if W1 has codimension k1, and W2 has codimension k2, then if U is their intersection with codimension j we have
- max (k1, k2) ≤ j ≤ k1 + k2.
In fact j may take any integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
value in this range. This statement is more perspicuous than the translation in terms of dimensions, because the RHS
Sides of an equation
In mathematics, LHS is informal shorthand for the left-hand side of an equation. Similarly, RHS is the right-hand side. Each is solely a name for a term as part of an expression; and they are in practice interchangeable, since equality is symmetric...
is just the sum of the codimensions. In words
- codimensions (at most) add.
- If the subspaces or submanifolds intersect transversally (which occurs genericallyGeneral positionIn algebraic geometry, general position is a notion of genericity for a set of points, or other geometric objects. It means the general case situation, as opposed to some more special or coincidental cases that are possible...
), codimensions add exactly.
This statement is called dimension counting, particularly in intersection theory.
Dual interpretation
In terms of the dual spaceDual space
In mathematics, any vector space, V, has a corresponding dual vector space consisting of all linear functionals on V. Dual vector spaces defined on finite-dimensional vector spaces can be used for defining tensors which are studied in tensor algebra...
, it is quite evident why dimensions add. The subspaces can be defined by the vanishing of a certain number of linear functional
Linear functional
In linear algebra, a linear functional or linear form is a linear map from a vector space to its field of scalars. In Rn, if vectors are represented as column vectors, then linear functionals are represented as row vectors, and their action on vectors is given by the dot product, or the...
s, which if we take to be linearly independent, their number is the codimension. Therefore we see that U is defined by taking the union
Union (set theory)
In set theory, the union of a collection of sets is the set of all distinct elements in the collection. The union of a collection of sets S_1, S_2, S_3, \dots , S_n\,\! gives a set S_1 \cup S_2 \cup S_3 \cup \dots \cup S_n.- Definition :...
of the sets of linear functionals defining the Wi. That union may introduce some degree of linear dependence: the possible values of j express that dependence, with the RHS sum being the case where there is no dependence. This definition of codimension in terms of the number of functions needed to cut out a subspace extends to situations in which both the ambient space and subspace are infinite dimensional.
In other language, which is basic for any kind of intersection theory
Intersection theory
In mathematics, intersection theory is a branch of algebraic geometry, where subvarieties are intersected on an algebraic variety, and of algebraic topology, where intersections are computed within the cohomology ring. The theory for varieties is older, with roots in Bézout's theorem on curves and...
, we are taking the union of a certain number of constraint
Constraint (mathematics)
In mathematics, a constraint is a condition that a solution to an optimization problem must satisfy. There are two types of constraints: equality constraints and inequality constraints...
s. We have two phenomena to look out for:
- the two sets of constraints may not be independent;
- the two sets of constraints may not be compatible.
The first of these is often expressed as the principle of counting constraints
Constraint (mathematics)
In mathematics, a constraint is a condition that a solution to an optimization problem must satisfy. There are two types of constraints: equality constraints and inequality constraints...
: if we have a number N of parameter
Parameter
Parameter from Ancient Greek παρά also “para” meaning “beside, subsidiary” and μέτρον also “metron” meaning “measure”, can be interpreted in mathematics, logic, linguistics, environmental science and other disciplines....
s to adjust (i.e. we have N degrees of freedom
Degrees of freedom (physics and chemistry)
A degree of freedom is an independent physical parameter, often called a dimension, in the formal description of the state of a physical system...
), and a constraint means we have to 'consume' a parameter to satisfy it, then the codimension of the solution set is at most the number of constraints. We do not expect to be able to find a solution if the predicted codimension, i.e. the number of independent constraints, exceeds N (in the linear algebra case, there is always a trivial, null vector
Null vector
Null vector can refer to:* Null vector * A causal structure in Minkowski space...
solution, which is therefore discounted).
The second is a matter of geometry, on the model of parallel lines
Parallel lines
Parallel Lines may refer to:*Parallel , two straight lines that never touch* Parallel Lines, an album by Blondie*Driver: Parallel Lines, a video game...
; it is something that can be discussed for linear problems by methods of linear algebra, and for non-linear problems in projective space
Projective space
In mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....
, over the complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
field.
In geometric topology
Codimension also has some clear meaning in geometric topologyGeometric topology
In mathematics, geometric topology is the study of manifolds and maps between them, particularly embeddings of one manifold into another.- Topics :...
: on a manifold, codimension 1 is the dimension of topological disconnection by a submanifold, while codimension 2 is the dimension of ramification
Ramification
In mathematics, ramification is a geometric term used for 'branching out', in the way that the square root function, for complex numbers, can be seen to have two branches differing in sign...
and knot theory
Knot theory
In topology, knot theory is the study of mathematical knots. While inspired by knots which appear in daily life in shoelaces and rope, a mathematician's knot differs in that the ends are joined together so that it cannot be undone. In precise mathematical language, a knot is an embedding of a...
. In fact, the theory of high dimensional manifolds, which starts in dimension 5 and above, can alternatively be said to start in codimension 3, because higher codimensions avoid the phenomenon of knots. Since surgery theory
Surgery theory
In mathematics, specifically in geometric topology, surgery theory is a collection of techniques used to produce one manifold from another in a 'controlled' way, introduced by . Surgery refers to cutting out parts of the manifold and replacing it with a part of another manifold, matching up along...
requires working up to the middle dimension, once one is in dimension 5, the middle dimension has codimension greater than 2, and hence one avoids knots.
This quip is not vacuous: the study of embeddings in codimension 2 is knot theory, and difficult, while the study of embeddings in codimension 3 or more is amenable to the tools of high dimensional geometric topology, and hence considerably easier.
To state the main topological codimension theorems more formally: in codimension 0, immersions may or may not exist; in codimension 1, immersions always exist but embedding
Embedding
In mathematics, an embedding is one instance of some mathematical structure contained within another instance, such as a group that is a subgroup....
s may or may not exist; in codimension 2, embedding
Embedding
In mathematics, an embedding is one instance of some mathematical structure contained within another instance, such as a group that is a subgroup....
s exist but may or may not be isotopic; in codimension 3 all embeddings are isotopic.

