
Topological vector space
Encyclopedia
In mathematics
, a topological vector space (also called a linear topological space) is one of the basic structures investigated in functional analysis
. As the name suggests the space blends a topological structure
(a uniform structure to be precise) with the algebra
ic concept of a vector space
.
The elements of topological vector spaces are typically function
s or linear operators acting on topological vector spaces, and the topology is often defined so as to capture a particular notion of convergence of sequences of functions.
Hilbert spaces and Banach spaces are well-known examples.
Unless stated otherwise, the underlying field of a topological vector space is assumed to be either or
or  .
.
over a topological field K (most often the real
or complex
numbers with their standard topologies) which is endowed with a topology
such that vector addition X × X → X and scalar multiplication K × X → X are continuous functions.
Some authors (e.g., Rudin
) require the topology on X to be T0; it then follows that the space is Hausdorff
, and even T3½
. The topological and linear algebraic structures can be tied together even more closely with additional assumptions, the most common of which are listed below.
The category of topological vector spaces over a given topological field K is commonly denoted TVSK or TVectK. The objects are the topological vector spaces over K and the morphism
s are the continuous K-linear maps from one object to another.
s, and therefore all Banach space
s and Hilbert space
s, are examples of topological vector spaces.
However, there are topological vector spaces whose topology is not induced by a norm but are still of interest in analysis. Examples of such spaces are spaces of holomorphic function
s on an open domain, spaces of infinitely differentiable functions, the Schwartz spaces, and spaces of test functions and the spaces of distributions
on them. These are all examples of Montel space
s. On the other hand, infinite dimensional Montel spaces are never normable.
A topological field is a topological vector space over each of its subfields.
of a family of topological vector spaces, when endowed with the product topology
is a topological vector space. For instance, the set X of all functions f : R → R. X can be identified with the product space RR and carries a natural product topology
. With this topology, X becomes a topological vector space, called the space of pointwise convergence
. The reason for this name is the following: if (fn) is a sequence of elements in X, then fn has limit
f in X if and only if fn(x) has limit f(x) for every real number x. This space is complete, but not normable: indeed, every neighborhood of 0 in the product topology contains lines, i.e., sets K f for f ≠ 0.
with respect to the operation of addition, and in a topological vector space the inverse operation is always continuous (since it is the same as multiplication by −1). Hence, every topological vector space is an abelian topological group
.
Let X be a topological vector space. Given a subspace , the quotient space X/M with the usual quotient topology is a Hausdorff topological vector space if and only if M is closed. This permits the following construction: given a topological vector space X (that is probably not Hausdorff), form the quotient space X / M where M is the closure of
, the quotient space X/M with the usual quotient topology is a Hausdorff topological vector space if and only if M is closed. This permits the following construction: given a topological vector space X (that is probably not Hausdorff), form the quotient space X / M where M is the closure of  . X / M is then a Hausdorff vector topological space that can be studied instead of X.
. X / M is then a Hausdorff vector topological space that can be studied instead of X.
In particular, topological vector spaces are uniform space
s and one can thus talk about completeness, uniform convergence and uniform continuity
. (This implies that every Hausdorff topological vector space is completely regular.) The vector space operations of addition and scalar multiplication are actually uniformly continuous. Because of this, every topological vector space can be completed and is thus a dense linear subspace
of a complete topological vector space.
A topological vector space is said to be normable if its topology can be induced by a norm. A topological vector space is normable if and only if it is Hausdorff and has a convex bounded neighbourhood of 0.
If a topological vector space is semi-metrizable, that is the topology can be given by a semi-metric, then the semi-metric can be chosen to be translation invariant. Also, a topological vector space is metrizable if and only if it is Hausdorff and has a countable local base (i.e., a neighborhood base at the origin).
A linear operator between two topological vector spaces which is continuous at one point is continuous on the whole domain. Moreover, a linear operator f is continuous if f(V) is bounded for some neighborhood V of 0.
A hyperplane on a topological vector space X is either dense or closed. A linear functional
f on a topological vector space X has either dense or closed kernel. Moreover, f is continuous if and only if its kernel
is closed
.
Every Hausdorff finite dimensional topological vector space is isomorphic to Kn for some topological field K. In particular, a Hausdorff topological vector space is finite-dimensional if and only if it is locally compact.
The definition of boundedness can be weakened a bit; E is bounded if and only if every countable subset of it is bounded. Also, E is bounded if and only if for every balanced neighborhood V of 0, there exists t such that . Moreover, when X is locally convex, the boundedness can be characterized by seminorms: the subset E is bounded iff every continuous semi-norm p is bounded on E.
. Moreover, when X is locally convex, the boundedness can be characterized by seminorms: the subset E is bounded iff every continuous semi-norm p is bounded on E.
Every topological vector space has a local base of absorbing
and balanced set
s.
A sequence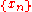 is said to be Cauchy
is said to be Cauchy
if for every neighborhood V of 0, the difference belongs to V when m and n are sufficiently large. Every Cauchy sequence is bounded, although Cauchy nets or Cauchy filters may not be bounded. A topological vector space where every Cauchy sequence converges is sequentially complete but may not be complete (in the sense Cauchy filters converge). Every compact set is bounded.
belongs to V when m and n are sufficiently large. Every Cauchy sequence is bounded, although Cauchy nets or Cauchy filters may not be bounded. A topological vector space where every Cauchy sequence converges is sequentially complete but may not be complete (in the sense Cauchy filters converge). Every compact set is bounded.
, the open mapping theorem
, and the fact that the dual space of the space separates points in the space.
Below are some common topological vector spaces, roughly ordered by their niceness.
. This may not be the only natural topology on the dual space; for instance, the dual of a Banach space has a natural norm defined on it. However, it is very important in applications because of its compactness properties (see Banach–Alaoglu theorem).
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a topological vector space (also called a linear topological space) is one of the basic structures investigated in functional analysis
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
. As the name suggests the space blends a topological structure
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
(a uniform structure to be precise) with the algebra
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
ic concept of a vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
.
The elements of topological vector spaces are typically function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
s or linear operators acting on topological vector spaces, and the topology is often defined so as to capture a particular notion of convergence of sequences of functions.
Hilbert spaces and Banach spaces are well-known examples.
Unless stated otherwise, the underlying field of a topological vector space is assumed to be either
 or
or  .
.Definition
A topological vector space X is a vector spaceVector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
over a topological field K (most often the real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
or complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
numbers with their standard topologies) which is endowed with a topology
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
such that vector addition X × X → X and scalar multiplication K × X → X are continuous functions.
Some authors (e.g., Rudin
Walter Rudin
Walter Rudin was an American mathematician, for most of his career a Professor of Mathematics at the University of Wisconsin–Madison....
) require the topology on X to be T0; it then follows that the space is Hausdorff
Hausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
, and even T3½
Tychonoff space
In topology and related branches of mathematics, Tychonoff spaces and completely regular spaces are kinds of topological spaces.These conditions are examples of separation axioms....
. The topological and linear algebraic structures can be tied together even more closely with additional assumptions, the most common of which are listed below.
The category of topological vector spaces over a given topological field K is commonly denoted TVSK or TVectK. The objects are the topological vector spaces over K and the morphism
Morphism
In mathematics, a morphism is an abstraction derived from structure-preserving mappings between two mathematical structures. The notion of morphism recurs in much of contemporary mathematics...
s are the continuous K-linear maps from one object to another.
Examples
All normed vector spaceNormed vector space
In mathematics, with 2- or 3-dimensional vectors with real-valued entries, the idea of the "length" of a vector is intuitive and can easily be extended to any real vector space Rn. The following properties of "vector length" are crucial....
s, and therefore all Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
s and Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
s, are examples of topological vector spaces.
However, there are topological vector spaces whose topology is not induced by a norm but are still of interest in analysis. Examples of such spaces are spaces of holomorphic function
Holomorphic function
In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
s on an open domain, spaces of infinitely differentiable functions, the Schwartz spaces, and spaces of test functions and the spaces of distributions
Distribution (mathematics)
In mathematical analysis, distributions are objects that generalize functions. Distributions make it possible to differentiate functions whose derivatives do not exist in the classical sense. In particular, any locally integrable function has a distributional derivative...
on them. These are all examples of Montel space
Montel space
In functional analysis and related areas of mathematics a Montel space, named after Paul Montel, is any topological vector space in which an analog of Montel's theorem holds. Specifically, a Montel space is a barrelled topological vector space where every closed and bounded set is compact...
s. On the other hand, infinite dimensional Montel spaces are never normable.
A topological field is a topological vector space over each of its subfields.
Product vector spaces
A cartesian productCartesian product
In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
of a family of topological vector spaces, when endowed with the product topology
Product topology
In topology and related areas of mathematics, a product space is the cartesian product of a family of topological spaces equipped with a natural topology called the product topology...
is a topological vector space. For instance, the set X of all functions f : R → R. X can be identified with the product space RR and carries a natural product topology
Product topology
In topology and related areas of mathematics, a product space is the cartesian product of a family of topological spaces equipped with a natural topology called the product topology...
. With this topology, X becomes a topological vector space, called the space of pointwise convergence
Pointwise convergence
In mathematics, pointwise convergence is one of various senses in which a sequence of functions can converge to a particular function.-Definition:...
. The reason for this name is the following: if (fn) is a sequence of elements in X, then fn has limit
Limit of a sequence
The limit of a sequence is, intuitively, the unique number or point L such that the terms of the sequence become arbitrarily close to L for "large" values of n...
f in X if and only if fn(x) has limit f(x) for every real number x. This space is complete, but not normable: indeed, every neighborhood of 0 in the product topology contains lines, i.e., sets K f for f ≠ 0.
Topological structure
A vector space is an abelian groupAbelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
with respect to the operation of addition, and in a topological vector space the inverse operation is always continuous (since it is the same as multiplication by −1). Hence, every topological vector space is an abelian topological group
Topological group
In mathematics, a topological group is a group G together with a topology on G such that the group's binary operation and the group's inverse function are continuous functions with respect to the topology. A topological group is a mathematical object with both an algebraic structure and a...
.
Let X be a topological vector space. Given a subspace
 , the quotient space X/M with the usual quotient topology is a Hausdorff topological vector space if and only if M is closed. This permits the following construction: given a topological vector space X (that is probably not Hausdorff), form the quotient space X / M where M is the closure of
, the quotient space X/M with the usual quotient topology is a Hausdorff topological vector space if and only if M is closed. This permits the following construction: given a topological vector space X (that is probably not Hausdorff), form the quotient space X / M where M is the closure of  . X / M is then a Hausdorff vector topological space that can be studied instead of X.
. X / M is then a Hausdorff vector topological space that can be studied instead of X.In particular, topological vector spaces are uniform space
Uniform space
In the mathematical field of topology, a uniform space is a set with a uniform structure. Uniform spaces are topological spaces with additional structure which is used to define uniform properties such as completeness, uniform continuity and uniform convergence.The conceptual difference between...
s and one can thus talk about completeness, uniform convergence and uniform continuity
Uniform continuity
In mathematics, a function f is uniformly continuous if, roughly speaking, it is possible to guarantee that f and f be as close to each other as we please by requiring only that x and y are sufficiently close to each other; unlike ordinary continuity, the maximum distance between x and y cannot...
. (This implies that every Hausdorff topological vector space is completely regular.) The vector space operations of addition and scalar multiplication are actually uniformly continuous. Because of this, every topological vector space can be completed and is thus a dense linear subspace
Linear subspace
The concept of a linear subspace is important in linear algebra and related fields of mathematics.A linear subspace is usually called simply a subspace when the context serves to distinguish it from other kinds of subspaces....
of a complete topological vector space.
A topological vector space is said to be normable if its topology can be induced by a norm. A topological vector space is normable if and only if it is Hausdorff and has a convex bounded neighbourhood of 0.
If a topological vector space is semi-metrizable, that is the topology can be given by a semi-metric, then the semi-metric can be chosen to be translation invariant. Also, a topological vector space is metrizable if and only if it is Hausdorff and has a countable local base (i.e., a neighborhood base at the origin).
A linear operator between two topological vector spaces which is continuous at one point is continuous on the whole domain. Moreover, a linear operator f is continuous if f(V) is bounded for some neighborhood V of 0.
A hyperplane on a topological vector space X is either dense or closed. A linear functional
Linear functional
In linear algebra, a linear functional or linear form is a linear map from a vector space to its field of scalars. In Rn, if vectors are represented as column vectors, then linear functionals are represented as row vectors, and their action on vectors is given by the dot product, or the...
f on a topological vector space X has either dense or closed kernel. Moreover, f is continuous if and only if its kernel
Kernel (algebra)
In the various branches of mathematics that fall under the heading of abstract algebra, the kernel of a homomorphism measures the degree to which the homomorphism fails to be injective. An important special case is the kernel of a matrix, also called the null space.The definition of kernel takes...
is closed
Closed set
In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
.
Every Hausdorff finite dimensional topological vector space is isomorphic to Kn for some topological field K. In particular, a Hausdorff topological vector space is finite-dimensional if and only if it is locally compact.
Local notions
A subset E of a topological vector space X is said to be- balancedBalanced setIn linear algebra and related areas of mathematics a balanced set, circled set or disk in a vector space is a set S so that for all scalars α with |α| ≤ 1\alpha S \subseteq S...
if for every scalar |t | ≤ 1
for every scalar |t | ≤ 1 - boundedBounded set (topological vector space)In functional analysis and related areas of mathematics, a set in a topological vector space is called bounded or von Neumann bounded, if every neighborhood of the zero vector can be inflated to include the set...
if for every neighborhood V of 0, then when t is sufficiently large.
when t is sufficiently large.
The definition of boundedness can be weakened a bit; E is bounded if and only if every countable subset of it is bounded. Also, E is bounded if and only if for every balanced neighborhood V of 0, there exists t such that
 . Moreover, when X is locally convex, the boundedness can be characterized by seminorms: the subset E is bounded iff every continuous semi-norm p is bounded on E.
. Moreover, when X is locally convex, the boundedness can be characterized by seminorms: the subset E is bounded iff every continuous semi-norm p is bounded on E.Every topological vector space has a local base of absorbing
Absorbing set
In functional analysis and related areas of mathematics an absorbing set in a vector space is a set S which can be inflated to include any element of the vector space...
and balanced set
Balanced set
In linear algebra and related areas of mathematics a balanced set, circled set or disk in a vector space is a set S so that for all scalars α with |α| ≤ 1\alpha S \subseteq S...
s.
A sequence
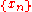 is said to be Cauchy
is said to be CauchyCauchy sequence
In mathematics, a Cauchy sequence , named after Augustin-Louis Cauchy, is a sequence whose elements become arbitrarily close to each other as the sequence progresses...
if for every neighborhood V of 0, the difference
 belongs to V when m and n are sufficiently large. Every Cauchy sequence is bounded, although Cauchy nets or Cauchy filters may not be bounded. A topological vector space where every Cauchy sequence converges is sequentially complete but may not be complete (in the sense Cauchy filters converge). Every compact set is bounded.
belongs to V when m and n are sufficiently large. Every Cauchy sequence is bounded, although Cauchy nets or Cauchy filters may not be bounded. A topological vector space where every Cauchy sequence converges is sequentially complete but may not be complete (in the sense Cauchy filters converge). Every compact set is bounded.Types of topological vector spaces
Depending on the application additional constraints are usually enforced on the topological structure of the space. In fact, several principal results in functional analysis fail to hold in general for topological vector spaces: the closed graph theoremClosed graph theorem
In mathematics, the closed graph theorem is a basic result in functional analysis which characterizes continuous linear operators between Banach spaces in terms of the operator graph.- The closed graph theorem :...
, the open mapping theorem
Open mapping theorem
Open mapping theorem may refer to:* Open mapping theorem or Banach–Schauder theorem states that a surjective continuous linear transformation of a Banach space X onto a Banach space Y is an open mapping...
, and the fact that the dual space of the space separates points in the space.
Below are some common topological vector spaces, roughly ordered by their niceness.
- Locally convex topological vector spaceLocally convex topological vector spaceIn functional analysis and related areas of mathematics, locally convex topological vector spaces or locally convex spaces are examples of topological vector spaces which generalize normed spaces. They can be defined as topological vector spaces whose topology is generated by translations of ...
s: here each point has a local base consisting of convex setConvex setIn Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
s. By a technique known as Minkowski functionalMinkowski functionalIn functional analysis, given a linear space X, a Minkowski functional is a device that uses the linear structure to introduce a topology on X.-Example 1:...
s it can be shown that a space is locally convex if and only if its topology can be defined by a family of semi-norms. Local convexity is the minimum requirement for "geometrical" arguments like the Hahn–Banach theoremHahn–Banach theoremIn mathematics, the Hahn–Banach theorem is a central tool in functional analysis. It allows the extension of bounded linear functionals defined on a subspace of some vector space to the whole space, and it also shows that there are "enough" continuous linear functionals defined on every normed...
. - Barrelled spaceBarrelled spaceIn functional analysis and related areas of mathematics, barrelled spaces are Hausdorff topological vector spaces for which every barrelled set in the space is a neighbourhood for the zero vector. A barrelled set or a barrel in a topological vector space is a set which is convex, balanced,...
s: locally convex spaces where the Banach–Steinhaus theorem holds. - Montel spaceMontel spaceIn functional analysis and related areas of mathematics a Montel space, named after Paul Montel, is any topological vector space in which an analog of Montel's theorem holds. Specifically, a Montel space is a barrelled topological vector space where every closed and bounded set is compact...
: a barrelled space where every closedClosed setIn geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
and bounded setBounded set (topological vector space)In functional analysis and related areas of mathematics, a set in a topological vector space is called bounded or von Neumann bounded, if every neighborhood of the zero vector can be inflated to include the set...
is compact - Bornological spaceBornological spaceIn mathematics, particularly in functional analysis, a bornological space is a type of space which, in some sense, possesses the minimum amount of structure needed to address questions of boundedness of sets and functions, in the same way that a topological space possesses the minimum amount of...
: a locally convex space where the continuous linear operatorContinuous linear operatorIn functional analysis and related areas of mathematics, a continuous linear operator or continuous linear mapping is a continuous linear transformation between topological vector spaces....
s to any locally convex space are exactly the bounded linear operators. - LF-spaceLF-spaceIn mathematics, an LF-space is a topological vector space V that is a countable strict inductive limit of Fréchet spaces. This means that for each n there is a subspace V_n such that-Properties:...
s are limitsLimit (category theory)In category theory, a branch of mathematics, the abstract notion of a limit captures the essential properties of universal constructions such as products and inverse limits....
of Fréchet spaces. ILH spaces are inverse limitInverse limitIn mathematics, the inverse limit is a construction which allows one to "glue together" several related objects, the precise manner of the gluing process being specified by morphisms between the objects...
s of Hilbert spaces. - F-spaceF-spaceIn functional analysis, an F-space is a vector space V over the real or complex numbers together with a metric d : V × V → R so that...
s are completeComplete spaceIn mathematical analysis, a metric space M is called complete if every Cauchy sequence of points in M has a limit that is also in M or, alternatively, if every Cauchy sequence in M converges in M....
topological vector spaces with a translation-invariant metric. These include Lp spacesLp spaceIn mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
for all p > 0. - Fréchet spaceFréchet spaceIn functional analysis and related areas of mathematics, Fréchet spaces, named after Maurice Fréchet, are special topological vector spaces. They are generalizations of Banach spaces...
s: these are complete locally convex spaces where the topology comes from a translation-invariant metric, or equivalently: from a countable family of semi-norms. Many interesting spaces of functions fall into this class. A locally convex F-space is a Fréchet space. - Nuclear spaceNuclear spaceIn mathematics, a nuclear space is a topological vector space with many of the good properties of finite-dimensional vector spaces. The topology on them can be defined by a family of seminorms whose unit balls decrease rapidly in size...
s: these are locally convex spaces with the property that every bounded map from the nuclear space to an arbitrary Banach space is a nuclear operatorNuclear operatorIn mathematics, a nuclear operator is roughly a compact operator for which a trace may be defined, such that the trace is finite and independent of the choice of basis .Nuclear operators are essentially the same as trace class operators, though most authors reserve the term "trace...
. - Normed spaces and semi-normed spaces: locally convex spaces where the topology can be described by a single normNorm (mathematics)In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
or semi-norm. In normed spaces a linear operator is continuous if and only if it is bounded. - Banach spaceBanach spaceIn mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
s: Complete normed vector spaceNormed vector spaceIn mathematics, with 2- or 3-dimensional vectors with real-valued entries, the idea of the "length" of a vector is intuitive and can easily be extended to any real vector space Rn. The following properties of "vector length" are crucial....
s. Most of functional analysis is formulated for Banach spaces. - Reflexive Banach spaceReflexive spaceIn functional analysis, a Banach space is called reflexive if it coincides with the dual of its dual space in the topological and algebraic senses. Reflexive Banach spaces are often characterized by their geometric properties.- Normed spaces :Suppose X is a normed vector space over R or C...
s: Banach spaces naturally isomorphic to their double dual (see below), which ensures that some geometrical arguments can be carried out. An important example which is not reflexive is L1, whose dual is L∞ but is strictly contained in the dual of L∞. - Hilbert spaceHilbert spaceThe mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
s: these have an inner product; even though these spaces may be infinite dimensional, most geometrical reasoning familiar from finite dimensions can be carried out in them. - Euclidean spaceEuclidean spaceIn mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
s: Rn or Cn with the topology induced by the standard inner product. As pointed out in the preceding section, for a given finite n, there is only one n-dimensional topological vector space, up to isomorphism. It follows from this that any finite dimensional subspace of a TVS is closed. A characterization of finite dimensionality is that a Hausdorff TVS is locally compact if and only if it is finite dimensional (therefore isomorphic to some Euclidean space).
Dual space
Every topological vector space has a continuous dual space—the set V∗ of all continuous linear functionals, i.e. continuous linear maps from the space into the base field K. A topology on the dual can be defined to be the coarsest topology such that the dual pairing V∗ × V → K is continuous. This turns the dual into a locally convex topological vector space. This topology is called the weak-* topologyWeak topology
In mathematics, weak topology is an alternative term for initial topology. The term is most commonly used for the initial topology of a topological vector space with respect to its continuous dual...
. This may not be the only natural topology on the dual space; for instance, the dual of a Banach space has a natural norm defined on it. However, it is very important in applications because of its compactness properties (see Banach–Alaoglu theorem).

