Fundamental lemma of calculus of variations
Encyclopedia
In mathematics
, specifically in the calculus of variations
, the fundamental lemma in the calculus of variations is a lemma
that is typically used to transform a problem from its weak formulation
(variational form) into its strong formulation (differential equation
).
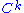
if it is k-times continuously differentiable. For example, class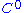
consists of continuous functions, and class 
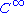consists of infinitely smooth functions.
Let f be of class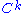
on the interval [a,b]. Assume furthermore that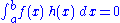
for every function h that is of class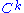
on [a,b] with h(a) = h(b) = 0. Then the fundamental lemma of the calculus of variations states that 
is identically zero on 
.
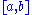In other words, the test functions h (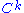
functions vanishing at the endpoints) separate 
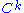functions: 
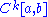is a Hausdorff space
in the weak topology
of pairing against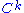
functions that vanish at the endpoints.
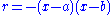. Let 
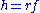. Then h is of class 
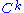on [a,b], so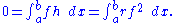
The integrand is nonnegative, so it must be 0 except perhaps on a subset of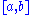
of measure 0. However, by continuity if there are points where the integrand is non-zero, there is also some interval around that point where the integrand is non-zero, which has non-zero measure, so it must be identically 0 over the entire interval. Since r is positive on (a, b), f is 0 there and hence on all of [a, b].
. Suppose that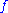
is a locally integrable function
defined on an open set
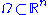. If
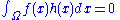
for all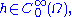
then f(x) = 0 for almost all x in Ω. Here, 
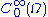is the space of all infinitely differentiable functions defined on Ω whose support
is a compact set contained in Ω.
of the functional
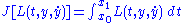
are weak solution
s of the Euler-Lagrange equation
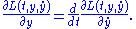
The Euler-Lagrange equation plays a prominent role in classical mechanics
and differential geometry.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, specifically in the calculus of variations
Calculus of variations
Calculus of variations is a field of mathematics that deals with extremizing functionals, as opposed to ordinary calculus which deals with functions. A functional is usually a mapping from a set of functions to the real numbers. Functionals are often formed as definite integrals involving unknown...
, the fundamental lemma in the calculus of variations is a lemma
Lemma (mathematics)
In mathematics, a lemma is a proven proposition which is used as a stepping stone to a larger result rather than as a statement in-and-of itself...
that is typically used to transform a problem from its weak formulation
Weak formulation
Weak formulations are an important tool for the analysis of mathematical equations that permit the transfer of concepts of linear algebra to solve problems in other fields such as partial differential equations...
(variational form) into its strong formulation (differential equation
Differential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
).
Statement
A function is said to be of class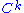Smooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
if it is k-times continuously differentiable. For example, class
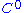consists of continuous functions, and class 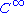consists of infinitely smooth functions.Let f be of class
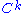on the interval [a,b]. Assume furthermore that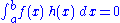for every function h that is of class
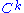on [a,b] with h(a) = h(b) = 0. Then the fundamental lemma of the calculus of variations states that is identically zero on 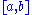.In other words, the test functions h (
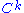functions vanishing at the endpoints) separate 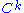functions: 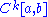is a Hausdorff spaceHausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
in the weak topology
Weak topology
In mathematics, weak topology is an alternative term for initial topology. The term is most commonly used for the initial topology of a topological vector space with respect to its continuous dual...
of pairing against
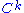functions that vanish at the endpoints.Proof
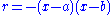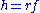Let f satisfy the hypotheses. Let r be any smooth function that is 0 at a and b and positive on (a, b); for example,. Let . Then h is of class 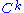on [a,b], so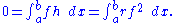The integrand is nonnegative, so it must be 0 except perhaps on a subset of
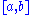of measure 0. However, by continuity if there are points where the integrand is non-zero, there is also some interval around that point where the integrand is non-zero, which has non-zero measure, so it must be identically 0 over the entire interval. Since r is positive on (a, b), f is 0 there and hence on all of [a, b].The du Bois-Reymond lemma
The du Bois-Reymond lemma (named after Paul du Bois-Reymond) is a more general version of the above lemma. It defines a sufficient condition to guarantee that a function vanishes almost everywhereAlmost everywhere
In measure theory , a property holds almost everywhere if the set of elements for which the property does not hold is a null set, that is, a set of measure zero . In cases where the measure is not complete, it is sufficient that the set is contained within a set of measure zero...
. Suppose that
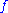is a locally integrable functionLocally integrable function
In mathematics, a locally integrable function is a function which is integrable on any compact set of its domain of definition. Their importance lies on the fact that we do not care about their behavior at infinity.- Formal definition :...
defined on an open set
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
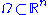. If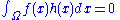for all
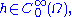then f(x) = 0 for almost all x in Ω. Here, 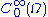is the space of all infinitely differentiable functions defined on Ω whose supportSupport (mathematics)
In mathematics, the support of a function is the set of points where the function is not zero, or the closure of that set . This concept is used very widely in mathematical analysis...
is a compact set contained in Ω.
Applications
This lemma is used to prove that extremaMaxima and minima
In mathematics, the maximum and minimum of a function, known collectively as extrema , are the largest and smallest value that the function takes at a point either within a given neighborhood or on the function domain in its entirety .More generally, the...
of the functional
Functional (mathematics)
In mathematics, and particularly in functional analysis, a functional is a map from a vector space into its underlying scalar field. In other words, it is a function that takes a vector as its input argument, and returns a scalar...
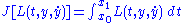
are weak solution
Weak solution
In mathematics, a weak solution to an ordinary or partial differential equation is a function for which the derivatives may not all exist but which is nonetheless deemed to satisfy the equation in some precisely defined sense. There are many different definitions of weak solution, appropriate for...
s of the Euler-Lagrange equation
Euler-Lagrange equation
In calculus of variations, the Euler–Lagrange equation, Euler's equation, or Lagrange's equation, is a differential equation whose solutions are the functions for which a given functional is stationary...
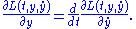
The Euler-Lagrange equation plays a prominent role in classical mechanics
Classical mechanics
In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
and differential geometry.