|
|
|
|
Integration by parts
|
| |
|
| |
In calculus, and more generally in mathematical analysis, integration by parts is a rule that transforms the integral of products of functions into other, hopefully simpler, integrals. The rule arises from the product rule of differentiation.
If u = f(x), v = g(x), and the differentials du = f '(x) dx and dv = g'(x) dx; then in its simplest form the product rule is:
The rule
Suppose f(x) and g(x) are two continuously differentiable functions.
Discussion
Ask a question about 'Integration by parts' Start a new discussion about 'Integration by parts' Answer questions from other users |
Encyclopedia
In calculus, and more generally in mathematical analysis, integration by parts is a rule that transforms the integral of products of functions into other, hopefully simpler, integrals. The rule arises from the product rule of differentiation.
If u = f(x), v = g(x), and the differentials du = f '(x) dx and dv = g'(x) dx; then in its simplest form the product rule is:
The rule
Suppose f(x) and g(x) are two continuously differentiable functions. The product rule states
Integrating both sides gives
Rearranging terms
From above one can derive integration by parts rule which states that given an interval with endpoints a, b, one has
where we use the common notation
The rule is shown to be true by using the product rule for derivatives and the fundamental theorem of calculus. Thus
-
In the traditional calculus curriculum, this rule is often stated using indefinite integrals in the form
or in an even shorter form, if we let u = f(x), v = g(x) and the differentials du = f ′(x) dx and dv = g′(x) dx, then it is in the form in which it is most often seen:
Note that the original integral contains the derivative of g; in order to be able to apply the rule, the antiderivative g must be found, and then the resulting integral ?g f′ dx must be evaluated.
One can also formulate a discrete analogue for sequences, called summation by parts.
An alternative notation has the advantage that the factors of the original expression are identified as f and g, but has the twin drawbacks of a nested integral and total unsuitability for the definite integral case:
This formula is valid whenever f is continuously differentiable and g is continuous.
More general formulations of integration by parts exist for the Riemann-Stieltjes integral and Lebesgue-Stieltjes integral.
Note: More complicated forms such as the one below are also valid:
Strategy
Integration by parts is a heuristic rather than a purely mechanical process for solving integrals; given a single function to integrate, the typical strategy is to carefully separate it into a product of two functions ƒ(x)g(x) such that the integral produced by the integration by parts formula is easier to evaluate than the original one. The following form is useful in illustrating the best strategy to take:
Note that on the right-hand side, ƒ is differentiated and g is integrated; consequently it is useful to choose ƒ as a function that simplifies when differentiated, and/or to choose g as a function that simplifies when integrated. As a simple example, consider:
Since ln x simplifies to 1/x when differentiated, we make this part of ƒ; since 1/x2 simplifies to −1/x when integrated, we make this part of g. The formula now yields:
The remaining integral of −1/x2 can be completed with the power rule and is 1/x.
Alternatively, we may choose ƒ and g such that the product simplifies due to cancellation. For example, suppose we wish to integrate:
If we choose ƒ(x) = ln(sin x) and g(x) = 1/(cos x)2, then ƒ differentiates to 1/tan x using the chain rule and g integrates to tan x; so the formula gives:
The integrand simplifies to 1, so the antiderivative is x. Finding a simplifying combination frequently involves experimentation.
In some applications, it may not be necessary to ensure that the integral produced by integration by parts has a simple form; for example, in numerical analysis, it may suffice that it has small magnitude and so contributes only a small error term. Some other special techniques are demonstrated in the examples below.
Examples
Integrands with powers of x or e x
In order to calculate:
Let:
- u = x, so du = dx,
- dv = cos(x) dx, so v = sin(x).
Then:
where C is an arbitrary constant of integration.
By repeatedly using integration by parts, integrals such as
can be computed in the same fashion: each application of the rule lowers the power of x by one.
An interesting example that is commonly seen is:
where, strangely enough, the actual integral does not need to be evaluated.
This example uses integration by parts twice. First let:
- u = cos(x); thus du = −sin(x) dx
- dv = ex dx; thus v = ex
Then:
Now, to evaluate the remaining integral, we use integration by parts again, with:
- u = sin(x); du = cos(x) dx
- v = ex; dv = ex dx
Then:
-
Putting these together, we get
Notice that the same integral shows up on both sides of this equation. So we can simply add the integral to both sides to get:
where, again, C (and C' = C/2) is an arbitrary constant of integration.
A similar trick is used to find the integral of secant cubed.
Interchange of the order of integration
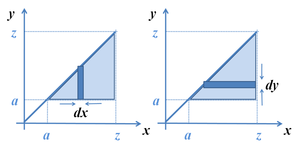
The above formulation includes the technique of interchange of the order of integration, which is not usually viewed in this manner. Consider the iterated integral:
In the order written above, the strip of width dx is integrated first over the y-direction as shown in the left panel of the figure, which is inconvenient especially when function h(y) is not easily integrated. The integral can be reduced to a single integration by reversing the order of integration as shown in the right panel of the figure. To accomplish this interchange of variables, the strip of width dy is first integrated from the line x = y to the limit x = z, and then the result is integrated from y = a to y = z, resulting in:
This result can be seen to be an example of the above formula for integration by parts, repeated below:
Substitute:
and
However, exchange of the order of integration has the merit that it generates the function f in a natural manner.
More examples
Two other well-known examples are when integration by parts is applied to a function expressed as a product of 1 and itself. This works if the derivative of the function is known, and the integral of this derivative times x is also known.
The first example is ? ln(x) dx. We write this as:
Let:
- u = ln(x); du = 1/x dx
- v = x; dv = 1·dx
Then:
-
where, again, C is the constant of integration.
The second example is ? arctan(x) dx, where arctan(x) is the inverse tangent function. Rewrite this as
Now let:
- u = arctan(x); du = 1/(1 + x2) dx
- v = x; dv = 1·dx
Then
-
using a combination of the inverse chain rule method and the natural logarithm integral condition.
Here is an example:
-
-
-
The LIATE rule
A rule of thumb developed in 1983 for choosing which of two functions is to be u is the LIATE rule. According to the rule, whichever function comes first in this list is to be u:
- L: logarithmic functions: ln x, log2(x), etc.
- I: inverse trigonometric functions: arctan x, arcsec x, etc.
- A: algebraic functions: , , etc.
- T: trigonometric functions: sin x, tan x, etc.
- E: exponential functions: , , etc.
The function which is to be dv by whichever function comes last in the list. You can remember the list by the mnemonic LIATE. The reason for this is that functions lower on the list have easier antiderivatives than the functions above them. This rule is sometimes seen reversed and written as DETAIL, with the D standing for dv and the following letters indicating the order in which the function dv should be chosen.
To demonstrate this rule, consider the integral
Following the LIATE rule, u = x and dv = cos x dx , hence du = dx and v = sin x , which makes the integral become
which equals
In general, one tries to choose u and dv such that du is simpler than u and dv is easy to integrate. If instead cos x was chosen as u and x as dv, we would have the integral
which, after recursive application of the integration by parts formula, would clearly result in an infinite recursion and lead nowhere.
Although a useful rule of thumb, there are exceptions to the LIATE rule. A common alternative is to consider the rules in the "ILATE" order instead. Also, in some cases, polynomial terms need to be split in non-trivial ways. For example, to integrate
we would set
This results in
Recursive integration by parts
Integration by parts can often be applied recursively on the term to provide the following formula
Here, is the first derivative of and is the second derivative of . Further, is a notation to describe its nth derivative (with respect to the variable u and v are functions of). Another notation has been adopted:
There are n + 1 integrals.
Note that the integrand above differs from the previous equation. The factor has been written as purely for convenience.
The above mentioned form is convenient because it can be evaluated by differentiating the first term and integrating the second (with a sign reversal each time), starting out with . It is very useful especially in cases when becomes zero for some k + 1. Hence, the integral evaluation can stop once the term has been reached.
Tabular integration by parts
While the aforementioned recursive definition is correct, it is often tedious to remember and implement. A much easier visual representation of this process is often taught to students and is dubbed either "the tabular method," "rapid repeated integration" or "the tic-tac-toe method." This method works best when one of the two functions in the product is a polynomial, that is, after differentiating it several times one obtains zero. It may also be extended to work for functions that will repeat themselves.
For example, consider the integral
Let u = x3. Begin with this function and list in a column all the subsequent derivatives until zero is reached. Secondly, begin with the function v (in this case cos(x) and list each integral of v until the size of the column is the same as that of u. The result should appear as follows.
| Derivatives of u (Column A) | Integrals of v (Column B) |
|---|
| | | | | | | | | | | | | | |
Now simply pair the 1st entry of column A with the 2nd entry of column B, the 2nd entry of column A with the 3rd entry of column B, etc... with alternating signs (beginning with the positive sign). Do so until further pairing is impossible. The result is the following (notice the alternating signs in each term):
Which, with simplification, leads to the result
With proper understanding of the tabular method, it can be extended. Consider
| Derivatives of u (Column A) | Integrals of v (Column B) |
|---|
| | | | | | | | |
In this case in the last step it is necessary to integrate the product of the two bottom cells obtaining:
which leads to
and gives the result.
Higher dimensions
The formula for integration by parts can be extended to functions of several variables. Instead of an interval one needs to integrate over a n-dimensional set. Also, one replaces the derivative with a partial derivative.
More specifically, suppose O is an open bounded subset of with a piecewise smooth boundary ?O. If u and v are two continuously differentiable functions on the closure of O, then the formula for integration by parts is
where is the outward unit surface normal to ?O, ?i is its i-th component, and i ranges from 1 to n. Replacing v in the above formula with vi and summing over i gives the vector formula
where v is a vector-valued function with components v1, ..., vn.
Setting u equal to the constant function 1 in the above formula gives the divergence theorem. For where , one gets
which is the first Green's identity.
The regularity requirements of the theorem can be relaxed. For instance, the boundary ?O need only be Lipschitz continuous. In the first formula above, only is necessary (where H1 is a Sobolev space); the other formulas have similarly relaxed requirements.
External links
|
| |
|
|
