Brans-Dicke theory
Encyclopedia
In theoretical physics
, the Brans–Dicke theory of gravitation (sometimes called the Jordan–Brans–Dicke theory) is a theoretical framework to explain gravitation
. It is a well-known competitor of Einstein
's more popular theory of general relativity
. It is an example of a scalar-tensor theory
, a gravitational theory in which the gravitational interaction is mediated by a scalar field
as well as the tensor field
of general relativity. The gravitational constant
G is not presumed to be constant but instead 1/G is replaced by a scalar field
which can vary from place to place and with time.
The theory was developed in 1961 by Robert H. Dicke
and Carl H. Brans
building upon, among others, the earlier 1959 work of Pascual Jordan
.
At present, both Brans–Dicke theory and general relativity are generally held to be in agreement with observation. Brans–Dicke theory represents a minority viewpoint in physics.
classical field theories of gravitation
, called metric theories. In these theories, spacetime
is equipped with a metric tensor
,
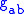, and the gravitational field is represented (in whole or in part) by the Riemann curvature tensor
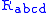, which is determined by the metric tensor.
All metric theories satisfy the Einstein equivalence principle
, which in modern geometric language states that in a very small region (too small to exhibit measurable curvature
effects), all the laws of physics known in special relativity
are valid in local Lorentz frames. This implies in turn that metric theories all exhibit the gravitational redshift
effect.
As in general relativity, the source of the gravitational field is considered to be the stress-energy tensor
or matter tensor. However, the way in which the immediate presence of mass-energy in some region affects the gravitational field in that region differs from general relativity. So does the way in which spacetime curvature affects the motion of matter. In the Brans–Dicke theory, in addition to the metric, which is a rank two tensor field, there is a scalar field,
, which has the physical effect of changing the effective gravitational constant from place to place. (This feature was actually a key desideratum of Dicke and Brans; see the paper by Brans cited below, which sketches the origins of the theory.)
The field equations of Brans–Dicke theory contain a parameter
,
, called the Brans–Dicke coupling constant. This is a true dimensionless constant
which must be chosen once and for all. However, it can be chosen to fit observations. Such parameters are often called tuneable parameters. In addition, the present ambient value of the effective gravitational constant must be chosen as a boundary condition. General relativity contains no dimensionless parameters whatsoever, and therefore is easier to falsify than Brans–Dicke theory. Theories with tuneable parameters are sometimes deprecated on the principle that, of two theories which both agree with observation, the more parsimonious is preferable. On the other hand, it seems as though they are a necessary feature of some theories, such as the weak mixing angle of the Standard Model
.
Brans–Dicke theory is "less stringent" than general relativity in another sense: it admits more solutions. In particular, exact vacuum solutions to the Einstein field equation of general relativity, augmented by the trivial scalar field
, become exact vacuum solutions in Brans–Dicke theory, but some spacetimes which are not vacuum solutions to the Einstein field equation become, with the appropriate choice of scalar field, vacuum solutions of Brans–Dicke theory. Similarly, an important class of spacetimes, the pp-wave metrics, are also exact null dust solution
s of both general relativity and Brans–Dicke theory, but here too, Brans–Dicke theory allows additional wave solutions having geometries which are incompatible with general relativity.
Like general relativity, Brans–Dicke theory predicts light deflection
and the precession
of perihelia
of planets orbiting the Sun. However, the precise formulas which govern these effects, according to Brans–Dicke theory, depend upon the value of the coupling constant
. This means that it is possible to set an observational lower bound on the possible value of 
from observations of the solar system and other gravitational systems. The value of 
consistent with experiment has risen with time. In 1973 
was consistent with known data. By 1981 
was consistent with known data. In 2003 evidence – derived from the Cassini–Huygens experiment – shows that the value of 
must exceed 40,000.
It is also often taught that general relativity is obtained from the Brans–Dicke theory in the limit
. But Faraoni (see references) claims that this breaks down when the trace of the stress-energy momentum vanishes, i.e.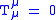 
. Some have argued that only general relativity satisfies the strong equivalence principle
.
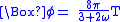
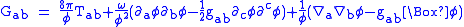
where
The first equation says that the trace of the stress-energy tensor acts as the source for the scalar field
. Since electromagnetic fields contribute only a traceless term to the stress-energy tensor,
this implies that in a region of spacetime containing only an electromagnetic field (plus the gravitational field), the right hand side vanishes, and
obeys the (curved spacetime) wave equation
. Therefore changes in
propagate through electrovacuum regions; in this sense, we say that 
is a long-range field.
The second equation describes how the stress-energy tensor and scalar field
together affect spacetime curvature. The left hand side, the Einstein tensor
, can be thought of as a kind of average curvature. It is a matter of pure mathematics that, in any metric theory, the Riemann tensor can always be written as the sum of the Weyl curvature (or conformal curvature tensor) plus a piece constructed from the Einstein tensor.
For comparison, the field equation of general relativity is simply
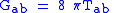
This means that in general relativity, the Einstein curvature at some event is entirely determined by the stress-energy tensor at that event; the other piece, the Weyl curvature, is the part of the gravitational field which can propagate as a gravitational wave across a vacuum region. But in the Brans–Dicke theory, the Einstein tensor is determined partly by the immediate presence of mass-energy and momentum, and partly by the long-range scalar field
.
The vacuum field equations of both theories are obtained when the stress-energy tensor vanishes. This models situations in which no non-gravitational fields are present.
contains the complete description of the Brans/Dicke theory:
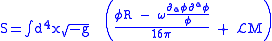
where
The matter term includes the contribution of ordinary matter (e.g. gaseous matter) and also electromagnetic fields. In a vacuum region, the matter term vanishes identically; the remaining term is the gravitational term. To obtain the vacuum field equations, we must vary the gravitational term in the Lagrangian with respect to the metric
; this gives the second field equation above. When we vary with respect to the scalar field 
, we obtain the first field equation.
Note that, unlike for the General Relativity field equations, the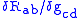
term does not vanish, as the result is not a total derivative. It can be shown that
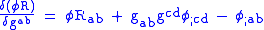
To prove this result, use
By evaluating the
s in Riemann normal coordinates, 6 individual terms vanish. 6 further terms combine when manipulated using Stokes' theorem
to provide the desired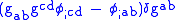
.
For comparison, the Lagrangian defining general relativity is
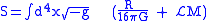
Varying the gravitational term with respect to
gives the vacuum Einstein field equation.
In both theories, the full field equations can be obtained by variations of the full Lagrangian.
Theoretical physics
Theoretical physics is a branch of physics which employs mathematical models and abstractions of physics to rationalize, explain and predict natural phenomena...
, the Brans–Dicke theory of gravitation (sometimes called the Jordan–Brans–Dicke theory) is a theoretical framework to explain gravitation
Gravitation
Gravitation, or gravity, is a natural phenomenon by which physical bodies attract with a force proportional to their mass. Gravitation is most familiar as the agent that gives weight to objects with mass and causes them to fall to the ground when dropped...
. It is a well-known competitor of Einstein
Albert Einstein
Albert Einstein was a German-born theoretical physicist who developed the theory of general relativity, effecting a revolution in physics. For this achievement, Einstein is often regarded as the father of modern physics and one of the most prolific intellects in human history...
's more popular theory of general relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
. It is an example of a scalar-tensor theory
Scalar-tensor theory
In theoretical physics, a scalar-tensor theory is a theory that includes both a scalar field and a tensor field to represent a certain interaction...
, a gravitational theory in which the gravitational interaction is mediated by a scalar field
Scalar field
In mathematics and physics, a scalar field associates a scalar value to every point in a space. The scalar may either be a mathematical number, or a physical quantity. Scalar fields are required to be coordinate-independent, meaning that any two observers using the same units will agree on the...
as well as the tensor field
Tensor field
In mathematics, physics and engineering, a tensor field assigns a tensor to each point of a mathematical space . Tensor fields are used in differential geometry, algebraic geometry, general relativity, in the analysis of stress and strain in materials, and in numerous applications in the physical...
of general relativity. The gravitational constant
Gravitational constant
The gravitational constant, denoted G, is an empirical physical constant involved in the calculation of the gravitational attraction between objects with mass. It appears in Newton's law of universal gravitation and in Einstein's theory of general relativity. It is also known as the universal...
G is not presumed to be constant but instead 1/G is replaced by a scalar field
which can vary from place to place and with time.The theory was developed in 1961 by Robert H. Dicke
Robert H. Dicke
Robert Henry Dicke was an American physicist who made important contributions to the fields of astrophysics, atomic physics, cosmology and gravity.-Biography:...
and Carl H. Brans
Carl H. Brans
Carl Henry Brans is an American mathematical physicist best known for his research into the theoretical underpinnings of gravitation elucidated in his most widely publicized work, the Brans–Dicke theory....
building upon, among others, the earlier 1959 work of Pascual Jordan
Pascual Jordan
-Further reading:...
.
At present, both Brans–Dicke theory and general relativity are generally held to be in agreement with observation. Brans–Dicke theory represents a minority viewpoint in physics.
Comparison with general relativity
Both Brans–Dicke theory and general relativity are examples of a class of relativisticTheory of relativity
The theory of relativity, or simply relativity, encompasses two theories of Albert Einstein: special relativity and general relativity. However, the word relativity is sometimes used in reference to Galilean invariance....
classical field theories of gravitation
Gravitation
Gravitation, or gravity, is a natural phenomenon by which physical bodies attract with a force proportional to their mass. Gravitation is most familiar as the agent that gives weight to objects with mass and causes them to fall to the ground when dropped...
, called metric theories. In these theories, spacetime
Spacetime
In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
is equipped with a metric tensor
Metric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
,
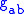, and the gravitational field is represented (in whole or in part) by the Riemann curvature tensorRiemann curvature tensor
In the mathematical field of differential geometry, the Riemann curvature tensor, or Riemann–Christoffel tensor after Bernhard Riemann and Elwin Bruno Christoffel, is the most standard way to express curvature of Riemannian manifolds...
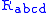, which is determined by the metric tensor.All metric theories satisfy the Einstein equivalence principle
Equivalence principle
In the physics of general relativity, the equivalence principle is any of several related concepts dealing with the equivalence of gravitational and inertial mass, and to Albert Einstein's assertion that the gravitational "force" as experienced locally while standing on a massive body is actually...
, which in modern geometric language states that in a very small region (too small to exhibit measurable curvature
Curvature
In mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...
effects), all the laws of physics known in special relativity
Special relativity
Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
are valid in local Lorentz frames. This implies in turn that metric theories all exhibit the gravitational redshift
Gravitational redshift
In astrophysics, gravitational redshift or Einstein shift describes light or other forms of electromagnetic radiation of certain wavelengths that originate from a source that is in a region of a stronger gravitational field that appear to be of longer wavelength, or redshifted, when seen or...
effect.
As in general relativity, the source of the gravitational field is considered to be the stress-energy tensor
Stress-energy tensor
The stress–energy tensor is a tensor quantity in physics that describes the density and flux of energy and momentum in spacetime, generalizing the stress tensor of Newtonian physics. It is an attribute of matter, radiation, and non-gravitational force fields...
or matter tensor. However, the way in which the immediate presence of mass-energy in some region affects the gravitational field in that region differs from general relativity. So does the way in which spacetime curvature affects the motion of matter. In the Brans–Dicke theory, in addition to the metric, which is a rank two tensor field, there is a scalar field,
, which has the physical effect of changing the effective gravitational constant from place to place. (This feature was actually a key desideratum of Dicke and Brans; see the paper by Brans cited below, which sketches the origins of the theory.)The field equations of Brans–Dicke theory contain a parameter
Parameter
Parameter from Ancient Greek παρά also “para” meaning “beside, subsidiary” and μέτρον also “metron” meaning “measure”, can be interpreted in mathematics, logic, linguistics, environmental science and other disciplines....
,
, called the Brans–Dicke coupling constant. This is a true dimensionless constantConstant (mathematics)
In mathematics, a constant is a non-varying value, i.e. completely fixed or fixed in the context of use. The term usually occurs in opposition to variable In mathematics, a constant is a non-varying value, i.e. completely fixed or fixed in the context of use. The term usually occurs in opposition...
which must be chosen once and for all. However, it can be chosen to fit observations. Such parameters are often called tuneable parameters. In addition, the present ambient value of the effective gravitational constant must be chosen as a boundary condition. General relativity contains no dimensionless parameters whatsoever, and therefore is easier to falsify than Brans–Dicke theory. Theories with tuneable parameters are sometimes deprecated on the principle that, of two theories which both agree with observation, the more parsimonious is preferable. On the other hand, it seems as though they are a necessary feature of some theories, such as the weak mixing angle of the Standard Model
Standard Model
The Standard Model of particle physics is a theory concerning the electromagnetic, weak, and strong nuclear interactions, which mediate the dynamics of the known subatomic particles. Developed throughout the mid to late 20th century, the current formulation was finalized in the mid 1970s upon...
.
Brans–Dicke theory is "less stringent" than general relativity in another sense: it admits more solutions. In particular, exact vacuum solutions to the Einstein field equation of general relativity, augmented by the trivial scalar field
, become exact vacuum solutions in Brans–Dicke theory, but some spacetimes which are not vacuum solutions to the Einstein field equation become, with the appropriate choice of scalar field, vacuum solutions of Brans–Dicke theory. Similarly, an important class of spacetimes, the pp-wave metrics, are also exact null dust solutionNull dust solution
In mathematical physics, a null dust solution is a Lorentzian manifold in which the Einstein tensor is null...
s of both general relativity and Brans–Dicke theory, but here too, Brans–Dicke theory allows additional wave solutions having geometries which are incompatible with general relativity.
Like general relativity, Brans–Dicke theory predicts light deflection
Gravitational lens
A gravitational lens refers to a distribution of matter between a distant source and an observer, that is capable of bending the light from the source, as it travels towards the observer...
and the precession
Precession
Precession is a change in the orientation of the rotation axis of a rotating body. It can be defined as a change in direction of the rotation axis in which the second Euler angle is constant...
of perihelia
Apsis
An apsis , plural apsides , is the point of greatest or least distance of a body from one of the foci of its elliptical orbit. In modern celestial mechanics this focus is also the center of attraction, which is usually the center of mass of the system...
of planets orbiting the Sun. However, the precise formulas which govern these effects, according to Brans–Dicke theory, depend upon the value of the coupling constant
. This means that it is possible to set an observational lower bound on the possible value of from observations of the solar system and other gravitational systems. The value of consistent with experiment has risen with time. In 1973 was consistent with known data. By 1981 was consistent with known data. In 2003 evidence – derived from the Cassini–Huygens experiment – shows that the value of must exceed 40,000.It is also often taught that general relativity is obtained from the Brans–Dicke theory in the limit
. But Faraoni (see references) claims that this breaks down when the trace of the stress-energy momentum vanishes, i.e. 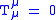. Some have argued that only general relativity satisfies the strong equivalence principleEquivalence principle
In the physics of general relativity, the equivalence principle is any of several related concepts dealing with the equivalence of gravitational and inertial mass, and to Albert Einstein's assertion that the gravitational "force" as experienced locally while standing on a massive body is actually...
.
The field equations
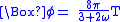
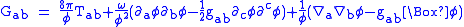
The field equations of the Brans/Dicke theory arewhere
is the dimensionless Dicke coupling constant,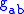
is the metric tensorMetric tensorIn the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
,
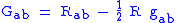is the Einstein tensorEinstein tensorIn differential geometry, the Einstein tensor , named after Albert Einstein, is used to express the curvature of a Riemannian manifold...
, a kind of average curvature,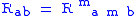
is the Ricci tensorRicci curvatureIn differential geometry, the Ricci curvature tensor, named after Gregorio Ricci-Curbastro, represents the amount by which the volume element of a geodesic ball in a curved Riemannian manifold deviates from that of the standard ball in Euclidean space...
, a kind of traceTrace (linear algebra)In linear algebra, the trace of an n-by-n square matrix A is defined to be the sum of the elements on the main diagonal of A, i.e.,...
of the curvature tensor,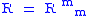
is the Ricci scalarScalar curvatureIn Riemannian geometry, the scalar curvature is the simplest curvature invariant of a Riemannian manifold. To each point on a Riemannian manifold, it assigns a single real number determined by the intrinsic geometry of the manifold near that point...
, the trace of the Ricci tensor,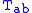
is the stress-energy tensorStress-energy tensorThe stress–energy tensor is a tensor quantity in physics that describes the density and flux of energy and momentum in spacetime, generalizing the stress tensor of Newtonian physics. It is an attribute of matter, radiation, and non-gravitational force fields...
,
is the trace of 
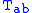, i.e. 
is the scalar field,
is the Laplace–Beltrami operator or covariant wave operator,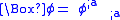 
The first equation says that the trace of the stress-energy tensor acts as the source for the scalar field
. Since electromagnetic fields contribute only a traceless term to the stress-energy tensor,this implies that in a region of spacetime containing only an electromagnetic field (plus the gravitational field), the right hand side vanishes, and
obeys the (curved spacetime) wave equationWave equation
The wave equation is an important second-order linear partial differential equation for the description of waves – as they occur in physics – such as sound waves, light waves and water waves. It arises in fields like acoustics, electromagnetics, and fluid dynamics...
. Therefore changes in
propagate through electrovacuum regions; in this sense, we say that is a long-range field.The second equation describes how the stress-energy tensor and scalar field
together affect spacetime curvature. The left hand side, the Einstein tensorEinstein tensor
In differential geometry, the Einstein tensor , named after Albert Einstein, is used to express the curvature of a Riemannian manifold...
, can be thought of as a kind of average curvature. It is a matter of pure mathematics that, in any metric theory, the Riemann tensor can always be written as the sum of the Weyl curvature (or conformal curvature tensor) plus a piece constructed from the Einstein tensor.
For comparison, the field equation of general relativity is simply
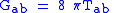
This means that in general relativity, the Einstein curvature at some event is entirely determined by the stress-energy tensor at that event; the other piece, the Weyl curvature, is the part of the gravitational field which can propagate as a gravitational wave across a vacuum region. But in the Brans–Dicke theory, the Einstein tensor is determined partly by the immediate presence of mass-energy and momentum, and partly by the long-range scalar field
.The vacuum field equations of both theories are obtained when the stress-energy tensor vanishes. This models situations in which no non-gravitational fields are present.
The action principle
The following LagrangianLagrangian
The Lagrangian, L, of a dynamical system is a function that summarizes the dynamics of the system. It is named after Joseph Louis Lagrange. The concept of a Lagrangian was originally introduced in a reformulation of classical mechanics by Irish mathematician William Rowan Hamilton known as...
contains the complete description of the Brans/Dicke theory:
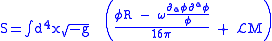
where
is the determinant of the metric,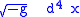
is the four-dimensional volume formVolume formIn mathematics, a volume form on a differentiable manifold is a nowhere-vanishing differential form of top degree. Thus on a manifold M of dimension n, a volume form is an n-form, a section of the line bundle Ωn = Λn, that is nowhere equal to zero. A manifold has a volume...
,
is the matter term or matter Lagrangian.
The matter term includes the contribution of ordinary matter (e.g. gaseous matter) and also electromagnetic fields. In a vacuum region, the matter term vanishes identically; the remaining term is the gravitational term. To obtain the vacuum field equations, we must vary the gravitational term in the Lagrangian with respect to the metric
; this gives the second field equation above. When we vary with respect to the scalar field , we obtain the first field equation.Note that, unlike for the General Relativity field equations, the
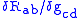term does not vanish, as the result is not a total derivative. It can be shown that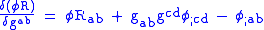To prove this result, use
By evaluating the
s in Riemann normal coordinates, 6 individual terms vanish. 6 further terms combine when manipulated using Stokes' theoremStokes' theorem
In differential geometry, Stokes' theorem is a statement about the integration of differential forms on manifolds, which both simplifies and generalizes several theorems from vector calculus. Lord Kelvin first discovered the result and communicated it to George Stokes in July 1850...
to provide the desired
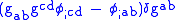.For comparison, the Lagrangian defining general relativity is
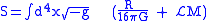
Varying the gravitational term with respect to
gives the vacuum Einstein field equation.In both theories, the full field equations can be obtained by variations of the full Lagrangian.
See also
- Classical theories of gravitationClassical theories of gravitationThe current Gold Standard Theory of Gravitation is the general theory of relativity. This is a classical, relativistic field theory of gravitation...
- Self-creation cosmologySelf-creation cosmologySelf-creation cosmology theories are gravitational theories in which the mass of the universe is created out of its self-contained gravitational and scalar fields, as opposed to the theory of continuous creation cosmology or the steady state theory which depend on an extra 'creation'...
, a modification of the Brans–Dicke theory that allows a non-minimally connected scalar field to interact with matter. - Mach's principleMach's principleIn theoretical physics, particularly in discussions of gravitation theories, Mach's principle is the name given by Einstein to an imprecise hypothesis often credited to the physicist and philosopher Ernst Mach....
- General relativityGeneral relativityGeneral relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...