Stress-energy tensor
Encyclopedia
Tensor
Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
quantity in physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
that describes the density
Density
The mass density or density of a material is defined as its mass per unit volume. The symbol most often used for density is ρ . In some cases , density is also defined as its weight per unit volume; although, this quantity is more properly called specific weight...
and flux
Flux
In the various subfields of physics, there exist two common usages of the term flux, both with rigorous mathematical frameworks.* In the study of transport phenomena , flux is defined as flow per unit area, where flow is the movement of some quantity per time...
of energy
Energy
In physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
and momentum
Momentum
In classical mechanics, linear momentum or translational momentum is the product of the mass and velocity of an object...
in spacetime
Spacetime
In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
, generalizing the stress tensor
Stress (physics)
In continuum mechanics, stress is a measure of the internal forces acting within a deformable body. Quantitatively, it is a measure of the average force per unit area of a surface within the body on which internal forces act. These internal forces are a reaction to external forces applied on the body...
of Newtonian physics. It is an attribute of matter
Matter
Matter is a general term for the substance of which all physical objects consist. Typically, matter includes atoms and other particles which have mass. A common way of defining matter is as anything that has mass and occupies volume...
, radiation
Radiation
In physics, radiation is a process in which energetic particles or energetic waves travel through a medium or space. There are two distinct types of radiation; ionizing and non-ionizing...
, and non-gravitational force fields. The stress-energy tensor is the source of the gravitational field
Gravitational field
The gravitational field is a model used in physics to explain the existence of gravity. In its original concept, gravity was a force between point masses...
in the Einstein field equations
Einstein field equations
The Einstein field equations or Einstein's equations are a set of ten equations in Albert Einstein's general theory of relativity which describe the fundamental interaction of gravitation as a result of spacetime being curved by matter and energy...
of general relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
, just as mass is the source of such a field in Newtonian gravity.
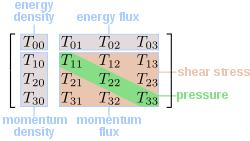
Definition
The stress–energy tensor involves the use of superscripted variables which are not exponents (see Einstein summation notationEinstein notation
In mathematics, especially in applications of linear algebra to physics, the Einstein notation or Einstein summation convention is a notational convention useful when dealing with coordinate formulae...
). The components of the position four-vector
Four-vector
In the theory of relativity, a four-vector is a vector in a four-dimensional real vector space, called Minkowski space. It differs from a vector in that it can be transformed by Lorentz transformations. The usage of the four-vector name tacitly assumes that its components refer to a standard basis...
are given by: x0 = t (time in seconds), x1 = x (in meters), x2 = y (in meters), and x3 = z (in meters).
The stress–energy tensor is defined as the tensor
Tensor
Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
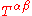of rank two that gives the fluxFlux
In the various subfields of physics, there exist two common usages of the term flux, both with rigorous mathematical frameworks.* In the study of transport phenomena , flux is defined as flow per unit area, where flow is the movement of some quantity per time...
of the αth component of the momentum
Momentum
In classical mechanics, linear momentum or translational momentum is the product of the mass and velocity of an object...
vector across a surface with constant xβ coordinate. In the theory of relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
, this momentum vector is taken as the four-momentum
Four-momentum
In special relativity, four-momentum is the generalization of the classical three-dimensional momentum to four-dimensional spacetime. Momentum is a vector in three dimensions; similarly four-momentum is a four-vector in spacetime...
. In general relativity, the stress-energy tensor is symmetric,
In some alternative theories like Einstein–Cartan theory
Einstein–Cartan theory
In theoretical physics, the Einstein–Cartan theory, also known as the Einstein–Cartan–Sciama–Kibble theory or the Cartan–Sciama–Kibble theory is a classical theory of gravitation similar to general relativity but relaxing the assumption that the metric be torsion-free. Introducing torsion allows...
, the stress–energy tensor may not be perfectly symmetric because of a nonzero spin tensor, which geometrically corresponds to a nonzero torsion tensor
Torsion tensor
In differential geometry, the notion of torsion is a manner of characterizing a twist or screw of a moving frame around a curve. The torsion of a curve, as it appears in the Frenet-Serret formulas, for instance, quantifies the twist of a curve about its tangent vector as the curve evolves In the...
.
Identifying the components of the tensor
In the following i and k range from 1 through 3.The time–time component is the density of relativistic mass, i.e. the energy density
Energy density
Energy density is a term used for the amount of energy stored in a given system or region of space per unit volume. Often only the useful or extractable energy is quantified, which is to say that chemically inaccessible energy such as rest mass energy is ignored...
divided by the speed of light squared,
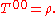
The flux of relativistic mass across the xi surface is equivalent to the density of the ith component of linear momentum,
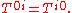
The components
represent flux of ith component of linear momentum across the xk surface. In particular,
(not summed) represents normal stress which is called pressure
Pressure
Pressure is the force per unit area applied in a direction perpendicular to the surface of an object. Gauge pressure is the pressure relative to the local atmospheric or ambient pressure.- Definition :...
when it is independent of direction. Whereas
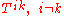
represents shear stress
Shear stress
A shear stress, denoted \tau\, , is defined as the component of stress coplanar with a material cross section. Shear stress arises from the force vector component parallel to the cross section...
(compare with the stress tensor
Stress (physics)
In continuum mechanics, stress is a measure of the internal forces acting within a deformable body. Quantitatively, it is a measure of the average force per unit area of a surface within the body on which internal forces act. These internal forces are a reaction to external forces applied on the body...
).
Warning: In solid state physics and fluid mechanics
Fluid mechanics
Fluid mechanics is the study of fluids and the forces on them. Fluid mechanics can be divided into fluid statics, the study of fluids at rest; fluid kinematics, the study of fluids in motion; and fluid dynamics, the study of the effect of forces on fluid motion...
, the stress tensor is defined to be the spatial components of
the stress–energy tensor in the comoving frame of reference. In other words, the stress energy tensor in engineering
Engineering
Engineering is the discipline, art, skill and profession of acquiring and applying scientific, mathematical, economic, social, and practical knowledge, in order to design and build structures, machines, devices, systems, materials and processes that safely realize improvements to the lives of...
differs from the stress energy tensor here by a momentum convective term.
Covariant and mixed forms
In most of this article we work with the contravariant form,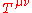
of the stress–energy tensor. However, it is often necessary to work with the covariant form
or the mixed form
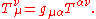
Or as a mixed tensor density
Tensor density
In differential geometry, a tensor density or relative tensor is a generalization of the tensor concept. A tensor density transforms as a tensor when passing from one coordinate system to another , except that it is additionally multiplied or weighted by a power of the Jacobian determinant of the...
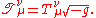
In special relativity
The stress–energy tensor is the conserved Noether currentNoether's theorem
Noether's theorem states that any differentiable symmetry of the action of a physical system has a corresponding conservation law. The theorem was proved by German mathematician Emmy Noether in 1915 and published in 1918...
associated with spacetime
Spacetime
In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
translation
Translation (physics)
In physics, translation is movement that changes the position of an object, as opposed to rotation. For example, according to Whittaker:...
s.
When gravity is negligible and using a Cartesian coordinate system
Cartesian coordinate system
A Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...
for spacetime, the divergence of the non-gravitational stress–energy will be zero. In other words, non-gravitational energy and momentum are conserved,
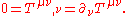
The integral form of this is
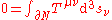
where N is any compact four-dimensional region of spacetime;
is its boundary, a three dimensional hypersurface; and 
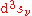is an element of the boundary regarded as the outward pointing normal.If one combines this with the symmetry of the stress–energy tensor, one can show that angular momentum
Angular momentum
In physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
is also conserved,
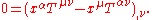
In general relativity
However, when gravity is non-negligible or when using arbitrary coordinate systems, the divergence of the non-gravitational stress-energy may fail to be zero. In this case, we have to use a more general continuity equationContinuity equation
A continuity equation in physics is a differential equation that describes the transport of a conserved quantity. Since mass, energy, momentum, electric charge and other natural quantities are conserved under their respective appropriate conditions, a variety of physical phenomena may be described...
which incorporates the covariant derivative
Covariant derivative
In mathematics, the covariant derivative is a way of specifying a derivative along tangent vectors of a manifold. Alternatively, the covariant derivative is a way of introducing and working with a connection on a manifold by means of a differential operator, to be contrasted with the approach given...
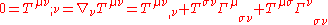
where
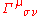is the Christoffel symbol which is the gravitational force field.Consequently, if
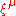is any Killing vector fieldKilling vector field
In mathematics, a Killing vector field , named after Wilhelm Killing, is a vector field on a Riemannian manifold that preserves the metric. Killing fields are the infinitesimal generators of isometries; that is, flows generated by Killing fields are continuous isometries of the manifold...
, then the conservation law associated with the symmetry generated by the Killing vector field may be expressed as
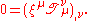
The integral form of this is
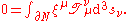
In general relativity
In general relativityGeneral relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
, the symmetric stress-energy tensor acts as the source of spacetime curvature
Riemann curvature tensor
In the mathematical field of differential geometry, the Riemann curvature tensor, or Riemann–Christoffel tensor after Bernhard Riemann and Elwin Bruno Christoffel, is the most standard way to express curvature of Riemannian manifolds...
, and is the current density associated with gauge transformations of gravity which are general curvilinear coordinate transformations. (If there is torsion
Torsion
The word torsion may refer to the following:*In geometry:** Torsion of a curve** Torsion tensor in differential geometry** The closely related concepts of Reidemeister torsion and analytic torsion ** Whitehead torsion*In algebra:** Torsion ** Tor functor* In medicine:** Ovarian...
, then the tensor is no longer symmetric. This corresponds to the case with a nonzero spin tensor in Einstein-Cartan gravity theory.)
In general relativity, the partial derivatives used in special relativity are replaced by covariant derivatives. What this means is that the continuity equation no longer implies that the non-gravitational energy and momentum expressed by the tensor are absolutely conserved, i.e. the gravitational field can do work on matter and vice versa. In the classical limit of Newtonian gravity, this has a simple interpretation: energy is being exchanged with gravitational potential energy
Potential energy
In physics, potential energy is the energy stored in a body or in a system due to its position in a force field or due to its configuration. The SI unit of measure for energy and work is the Joule...
, which is not included in the tensor, and momentum is being transferred through the field to other bodies. In general relativity the Landau–Lifshitz pseudotensor is a unique way to define the gravitational field energy and momentum densities. Any such stress-energy pseudotensor can be made to vanish locally by a coordinate transformation.
In curved spacetime, the spacelike integral
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
now depends on the spacelike slice, in general. There is in fact no way to define a global energy-momentum vector in a general curved spacetime.
The Einstein field equations
In general relativity, the stress tensor is studied in the context of the Einstein field equations which are often written as
where
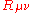is the Ricci tensor, 
is the Ricci scalar (the tensor contractionTensor contraction
In multilinear algebra, a tensor contraction is an operation on one or more tensors that arises from the natural pairing of a finite-dimensional vector space and its dual. In components, it is expressed as a sum of products of scalar components of the tensor caused by applying the summation...
of the Ricci tensor), and
is the universal gravitational constant.Isolated particle
In special relativity, the stress-energy of a non-interacting particle with mass m and trajectory
is:
where
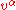is the velocity vector (which should not be confused with four-velocityFour-velocity
In physics, in particular in special relativity and general relativity, the four-velocity of an object is a four-vector that replaces classicalvelocity...
)
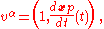
δ is the Dirac delta function
Dirac delta function
The Dirac delta function, or δ function, is a generalized function depending on a real parameter such that it is zero for all values of the parameter except when the parameter is zero, and its integral over the parameter from −∞ to ∞ is equal to one. It was introduced by theoretical...
and
is the energyEnergy
In physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
of the particle.
Stress-energy of a fluid in equilibrium
For a fluid in thermodynamic equilibriumThermodynamic equilibrium
In thermodynamics, a thermodynamic system is said to be in thermodynamic equilibrium when it is in thermal equilibrium, mechanical equilibrium, radiative equilibrium, and chemical equilibrium. The word equilibrium means a state of balance...
, the stress-energy tensor takes on a particularly simple form
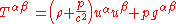
where
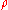is the mass-energy density (kilograms per cubic meter), 
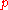is the hydrostatic pressure (pascalsPascal (unit)
The pascal is the SI derived unit of pressure, internal pressure, stress, Young's modulus and tensile strength, named after the French mathematician, physicist, inventor, writer, and philosopher Blaise Pascal. It is a measure of force per unit area, defined as one newton per square metre...
),
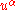is the fluid's four velocity, and 
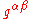is the reciprocal of the metric tensorMetric tensor (general relativity)
In general relativity, the metric tensor is the fundamental object of study. It may loosely be thought of as a generalization of the gravitational field familiar from Newtonian gravitation...
.
The four velocity satisfies
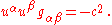
In an inertial frame of reference
Inertial frame of reference
In physics, an inertial frame of reference is a frame of reference that describes time homogeneously and space homogeneously, isotropically, and in a time-independent manner.All inertial frames are in a state of constant, rectilinear motion with respect to one another; they are not...
comoving with the fluid, the four velocity is
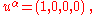
the reciprocal of the metric tensor is simply
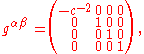
and the stress-energy tensor is a diagonal matrix
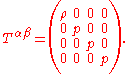
Electromagnetic stress-energy tensor
The stress-energy tensor of a source-free electromagnetic field is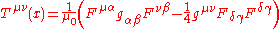
where
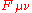is the electromagnetic field tensor.Scalar field
The stress-energy tensor for a scalar field
which satisfies the Klein–Gordon equation is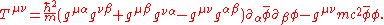
Variant definitions of stress-energy
There are a number of inequivalent definitions of non-gravitational stress-energy:Hilbert stress-energy tensor
This stress-energy tensor can only be defined in general relativityGeneral relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
with a dynamical metric. It is defined as a functional derivative
Functional derivative
In mathematics and theoretical physics, the functional derivative is a generalization of the gradient. While the latter differentiates with respect to a vector with discrete components, the former differentiates with respect to a continuous function. Both of these can be viewed as extensions of...
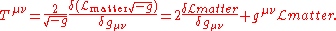
where Lmatter is the nongravitational part of the Lagrangian
Lagrangian
The Lagrangian, L, of a dynamical system is a function that summarizes the dynamics of the system. It is named after Joseph Louis Lagrange. The concept of a Lagrangian was originally introduced in a reformulation of classical mechanics by Irish mathematician William Rowan Hamilton known as...
density of the action
Action (physics)
In physics, action is an attribute of the dynamics of a physical system. It is a mathematical functional which takes the trajectory, also called path or history, of the system as its argument and has a real number as its result. Action has the dimension of energy × time, and its unit is...
. This is symmetric and gauge-invariant. See Einstein–Hilbert action for more information.
Canonical stress-energy tensor
Noether's theoremNoether's theorem
Noether's theorem states that any differentiable symmetry of the action of a physical system has a corresponding conservation law. The theorem was proved by German mathematician Emmy Noether in 1915 and published in 1918...
implies that there is a conserved current associated with translations through space and time. This is called the canonical stress-energy tensor. Generally, this is not symmetric and if we have some gauge theory, it may not be gauge invariant because space-dependent gauge transformations do not commute with spatial translations.
In general relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
, the translations are with respect to the coordinate system and as such, do not transform covariantly. See the section below on the gravitational stress-energy pseudo-tensor.
Belinfante–Rosenfeld stress–energy tensor
In the presence of spin or other intrinsic angular momentum, the canonical Noether stress energy tensor fails to be symmetric. The Belinfante–Rosenfeld stress energy tensor is constructed from the canonical stress-energy tensor and the spin current in such a way as to be symmetric and still conserved. In general relativity , this modified tensor agrees with the Hilbert stress–energy tensor. See the article Belinfante–Rosenfeld stress-energy tensorBelinfante–Rosenfeld stress-energy tensor
In mathematical physics, the Belinfante–Rosenfeld tensor is a modification of the energy-momentum tensor that is constructed from the canonical energy-momentum tensor and the spin current so as to be symmetric yet still conserved....
for more details.
Gravitational stress-energy
By the equivalence principleEquivalence principle
In the physics of general relativity, the equivalence principle is any of several related concepts dealing with the equivalence of gravitational and inertial mass, and to Albert Einstein's assertion that the gravitational "force" as experienced locally while standing on a massive body is actually...
gravitational stress-energy will always vanish locally at any chosen point in some chosen frame, therefore gravitational stress-energy cannot be expressed as a non-zero tensor; instead we have to use a pseudotensor
Pseudotensor
In physics and mathematics, a pseudotensor is usually a quantity that transforms like a tensor under an orientation preserving coordinate transformation , but gains an additional sign flip under an orientation reversing coordinate transformation In physics and mathematics, a pseudotensor is usually...
.
In general relativity, there are many possible distinct definitions of the gravitational stress-energy-momentum pseudotensor
Pseudotensor
In physics and mathematics, a pseudotensor is usually a quantity that transforms like a tensor under an orientation preserving coordinate transformation , but gains an additional sign flip under an orientation reversing coordinate transformation In physics and mathematics, a pseudotensor is usually...
. These include the Einstein pseudotensor and the Landau–Lifshitz pseudotensor. The Landau–Lifshitz pseudotensor can be reduced to zero at any event in spacetime by choosing an appropriate coordinate system.
See also
- Cooperstock's Energy Localization HypothesisCooperstock's Energy Localization HypothesisIn physics, the Cooperstock's energy-localization hypothesis is a hypothesis proposed by Fred Cooperstock that in general relativity, energy only exists in regions of non-vanishing energy–momentum tensor....
- Electromagnetic stress-energy tensor
- Energy conditionEnergy conditionIn relativistic classical field theories of gravitation, particularly general relativity, an energy condition is one of various alternative conditions which can be applied to the matter content of the theory, when it is either not possible or desirable to specify this content explicitly...
- Energy density of electric and magnetic fields
- Maxwell stress tensorMaxwell stress tensorThe Maxwell Stress Tensor is a mathematical object in physics, more precisely it is a second rank tensor used in classical electromagnetism to represent the interaction between electric/magnetic forces and mechanical momentum...
- Poynting vectorPoynting vectorIn physics, the Poynting vector can be thought of as representing the directional energy flux density of an electromagnetic field. It is named after its inventor John Henry Poynting. Oliver Heaviside and Nikolay Umov independently co-invented the Poynting vector...
- Segre classificationSegre classificationThe Segre classification is an algebraic classification of rank two symmetric tensors. The resulting types are then known as Segre types. It is most commonly applied to the energy-momentum tensor and primarily finds application in the classification of exact solutions in general relativity....
External links
- Lecture, Stephan Waner
- Caltech Tutorial on Relativity — A simple discussion of the relation between the Stress-Energy tensor of General Relativity and the metric