Apsis
Encyclopedia
An apsis plural apsides (icon; Greek: ἁψίδες), is the point of greatest or least distance of a body from one of the foci
of its elliptical orbit. In modern celestial mechanics
this focus is also the center of attraction, which is usually the center of mass
of the system. Historically, in geocentric systems
, apsides were measured from the center of the Earth.
The point of closest approach (the point at which two bodies are the closest) is called the periapsis or pericentre, from Greek , peri, around, and κέντρον kentron. The point of farthest excursion is called the apoapsis ' onMouseout='HidePop("99463")' href="/topics/Spiritus_lenis">unaspirated
, or , aph-, before an aspirated vowel
, respectively]), (the latter term, although etymologically more correct, is much less used). A straight line drawn through the periapsis and apoapsis is the line of apsides. This is the major axis of the ellipse
, the line through the longest part of the ellipse.
Derivative terms are used to identify the body being orbited. The most common are perigee icon and apogee icon, referring to orbits around the Earth
(Greek , gê, "earth"), and perihelion icon and aphelion icon, referring to orbits around the Sun
(Greek , hēlios, "sun"). During the Apollo program, the terms pericynthion and apocynthion were used when referring to the Moon
.
These formula
s characterize the periapsis and apoapsis of an orbit:
while, in accordance with Kepler's laws of planetary motion
(based on the conservation of angular momentum
) and the conservation of energy, these two quantities are constant for a given orbit:
where:
Note that for conversion from heights above the surface to distances between an orbit and its primary, the radius of the central body has to be added, and conversely.
The arithmetic mean
of the two limiting distances is the length of the semi-major axis
.
The geometric mean
of the two distances is the length of the semi-minor axis
.
The geometric mean of the two limiting speeds is
, the speed corresponding to a kinetic energy which, at any position of the orbit, added to the existing kinetic energy, would allow the orbiting body to escape (the square root of the product of the two speeds is the local escape velocity
).
Various related terms are used for other celestial objects
. The '-gee', '-helion' and '-astron' and '-galacticon' forms are frequently used in the astronomical literature, while the other listed forms are occasionally used, although '-saturnium' has very rarely been used in the last 50 years. The '-gee' form is commonly (although incorrectly) used as a generic 'closest approach to planet' term instead of specifically applying to the Earth. The term peri/apomelasma (from the Greek root) was used by physicist Geoffrey A. Landis
in 1998 before peri/aponigricon (from the Latin) appeared in the scientific literature in 2002.
Since "peri" and "apo" are Greek, it is considered by some purists more correct to use the Greek form for the body, giving forms such as '-zene' for Jupiter and '-krone' for Saturn. The daunting prospect of having to maintain a different word for every orbitable body in the Solar System (and beyond) is the main reason why the generic '-apsis' has become the almost universal norm in cases other than the Sun and Earth.
.
Currently, the annual perihelion happens at about 14 days after the December Solstice, thus on or about January 4. At perihelion, the Earth is about 0.98329 astronomical unit
s (AU) or 147,098,070 kilometers (about 91,402,500 miles) from the sun. (The eccentricity
of the orbit also varies slowly over many millennia.)
Likewise, the annual aphelion currently occurs in early July, about 14 days after the June Solstice. At this time, the distance of the aphelion is currently about 1.01671 AU or 152097700 kilometres (94,509,364.1 mi).
On a very long time scale, the dates of the perihelion and of the aphelion progress through the seasons, and they make one complete cycle in 22,000 to 26,000 years. There is a corresponding movement of the position of the stars as seen from Earth that is called the apsidal precession
. (This is not the precession of the axis.)
Astronomers commonly express the timing of perihelion relative to the vernal equinox not in terms of days and hours, but rather as an angle of orbital displacement, the so-called longitude of the periapsis
. For the orbit of the Earth, this is called the longitude of perihelion, and in the year 2000 was about 282.895 degrees. By the year 2010, this had advanced by a small fraction of a degree to about 283.067 degrees.
The dates and times of the perihelions and aphelions for several past and future years are listed in the following table:
s and dwarf planet
s from the Sun at their perihelion and aphelion.
The following chart shows the range of distances of the planets, dwarf planets and Halley's Comet from the Sun.
The images below show the perihelion and aphelion points of the inner and outer planets.
Conic section
In mathematics, a conic section is a curve obtained by intersecting a cone with a plane. In analytic geometry, a conic may be defined as a plane algebraic curve of degree 2...
of its elliptical orbit. In modern celestial mechanics
Celestial mechanics
Celestial mechanics is the branch of astronomy that deals with the motions of celestial objects. The field applies principles of physics, historically classical mechanics, to astronomical objects such as stars and planets to produce ephemeris data. Orbital mechanics is a subfield which focuses on...
this focus is also the center of attraction, which is usually the center of mass
Center of mass
In physics, the center of mass or barycenter of a system is the average location of all of its mass. In the case of a rigid body, the position of the center of mass is fixed in relation to the body...
of the system. Historically, in geocentric systems
Geocentric model
In astronomy, the geocentric model , is the superseded theory that the Earth is the center of the universe, and that all other objects orbit around it. This geocentric model served as the predominant cosmological system in many ancient civilizations such as ancient Greece...
, apsides were measured from the center of the Earth.
The point of closest approach (the point at which two bodies are the closest) is called the periapsis or pericentre, from Greek , peri, around, and κέντρον kentron. The point of farthest excursion is called the apoapsis ' onMouseout='HidePop("99463")' href="/topics/Spiritus_lenis">unaspirated
Spiritus lenis
The smooth breathing is a diacritical mark used in polytonic orthography. In ancient Greek, it marks the absence of the voiceless glottal fricative from the beginning of a word....
, or , aph-, before an aspirated vowel
Spiritus asper
In the polytonic orthography of Ancient Greek, the rough breathing , is a diacritical mark used to indicate the presence of an sound before a vowel, diphthong, or rho. It remained in the polytonic orthography even after the Hellenistic period, when the sound disappeared from the Greek language...
, respectively]), (the latter term, although etymologically more correct, is much less used). A straight line drawn through the periapsis and apoapsis is the line of apsides. This is the major axis of the ellipse
Ellipse
In geometry, an ellipse is a plane curve that results from the intersection of a cone by a plane in a way that produces a closed curve. Circles are special cases of ellipses, obtained when the cutting plane is orthogonal to the cone's axis...
, the line through the longest part of the ellipse.
Derivative terms are used to identify the body being orbited. The most common are perigee icon and apogee icon, referring to orbits around the Earth
Earth
Earth is the third planet from the Sun, and the densest and fifth-largest of the eight planets in the Solar System. It is also the largest of the Solar System's four terrestrial planets...
(Greek , gê, "earth"), and perihelion icon and aphelion icon, referring to orbits around the Sun
Sun
The Sun is the star at the center of the Solar System. It is almost perfectly spherical and consists of hot plasma interwoven with magnetic fields...
(Greek , hēlios, "sun"). During the Apollo program, the terms pericynthion and apocynthion were used when referring to the Moon
Moon
The Moon is Earth's only known natural satellite,There are a number of near-Earth asteroids including 3753 Cruithne that are co-orbital with Earth: their orbits bring them close to Earth for periods of time but then alter in the long term . These are quasi-satellites and not true moons. For more...
.
Mathematical formulas
Formula
In mathematics, a formula is an entity constructed using the symbols and formation rules of a given logical language....
s characterize the periapsis and apoapsis of an orbit:
- Periapsis: maximum speed
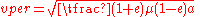at minimum (periapsis) distance 
- Apoapsis: minimum speed
at maximum (apoapsis) distance 
while, in accordance with Kepler's laws of planetary motion
Kepler's laws of planetary motion
In astronomy, Kepler's laws give a description of the motion of planets around the Sun.Kepler's laws are:#The orbit of every planet is an ellipse with the Sun at one of the two foci....
(based on the conservation of angular momentum
Angular momentum
In physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
) and the conservation of energy, these two quantities are constant for a given orbit:
- specific relative angular momentumSpecific relative angular momentumThe specific relative angular momentum is also known as the areal momentum .In astrodynamics, the specific relative angular momentum of two orbiting bodies is the vector product of the relative position and the relative velocity. Equivalently, it is the total angular momentum divided by the...
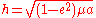
- specific orbital energySpecific orbital energyIn the gravitational two-body problem, the specific orbital energy \epsilon\,\! of two orbiting bodies is the constant sum of their mutual potential energy and their total kinetic energy , divided by the reduced mass...
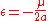
where:
-
is the semi-major axisSemi-major axisThe major axis of an ellipse is its longest diameter, a line that runs through the centre and both foci, its ends being at the widest points of the shape... -
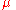is the standard gravitational parameterStandard gravitational parameterIn astrodynamics, the standard gravitational parameter μ of a celestial body is the product of the gravitational constant G and the mass M of the body.\mu=GM \ The SI units of the standard gravitational parameter are m3s−2.... -
is the eccentricityOrbital eccentricityThe orbital eccentricity of an astronomical body is the amount by which its orbit deviates from a perfect circle, where 0 is perfectly circular, and 1.0 is a parabola, and no longer a closed orbit...
, defined as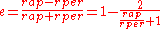
Note that for conversion from heights above the surface to distances between an orbit and its primary, the radius of the central body has to be added, and conversely.
The arithmetic mean
Arithmetic mean
In mathematics and statistics, the arithmetic mean, often referred to as simply the mean or average when the context is clear, is a method to derive the central tendency of a sample space...
of the two limiting distances is the length of the semi-major axis
Semi-major axis
The major axis of an ellipse is its longest diameter, a line that runs through the centre and both foci, its ends being at the widest points of the shape...
.The geometric mean
Geometric mean
The geometric mean, in mathematics, is a type of mean or average, which indicates the central tendency or typical value of a set of numbers. It is similar to the arithmetic mean, except that the numbers are multiplied and then the nth root of the resulting product is taken.For instance, the...
of the two distances is the length of the semi-minor axis
Semi-minor axis
In geometry, the semi-minor axis is a line segment associated with most conic sections . One end of the segment is the center of the conic section, and it is at right angles with the semi-major axis...
.The geometric mean of the two limiting speeds is
, the speed corresponding to a kinetic energy which, at any position of the orbit, added to the existing kinetic energy, would allow the orbiting body to escape (the square root of the product of the two speeds is the local escape velocityEscape velocity
In physics, escape velocity is the speed at which the kinetic energy plus the gravitational potential energy of an object is zero gravitational potential energy is negative since gravity is an attractive force and the potential is defined to be zero at infinity...
).
Terminology
The words "pericenter" and "apocenter" are occasionally seen, although periapsis/apoapsis are preferred in technical usage.Various related terms are used for other celestial objects
Celestial Body
Celestial Body is a Croatian film directed by Lukas Nola. It was released in 2000....
. The '-gee', '-helion' and '-astron' and '-galacticon' forms are frequently used in the astronomical literature, while the other listed forms are occasionally used, although '-saturnium' has very rarely been used in the last 50 years. The '-gee' form is commonly (although incorrectly) used as a generic 'closest approach to planet' term instead of specifically applying to the Earth. The term peri/apomelasma (from the Greek root) was used by physicist Geoffrey A. Landis
Geoffrey A. Landis
Geoffrey A. Landis is an American scientist, working for the National Aeronautics and Space Administration on planetary exploration, interstellar propulsion, solar power and photovoltaics...
in 1998 before peri/aponigricon (from the Latin) appeared in the scientific literature in 2002.
| Body | Closest approach | Farthest approach |
|---|---|---|
| General | Periapsis/Pericentre | Apoapsis |
| Galaxy Galaxy A galaxy is a massive, gravitationally bound system that consists of stars and stellar remnants, an interstellar medium of gas and dust, and an important but poorly understood component tentatively dubbed dark matter. The word galaxy is derived from the Greek galaxias , literally "milky", a... |
Perigalacticon | Apogalacticon |
| Star Star A star is a massive, luminous sphere of plasma held together by gravity. At the end of its lifetime, a star can also contain a proportion of degenerate matter. The nearest star to Earth is the Sun, which is the source of most of the energy on Earth... |
Periastron | Apastron |
| Black hole Black hole A black hole is a region of spacetime from which nothing, not even light, can escape. The theory of general relativity predicts that a sufficiently compact mass will deform spacetime to form a black hole. Around a black hole there is a mathematically defined surface called an event horizon that... |
Perimelasma/Peribothra/Perinigricon | Apomelasma/Apobothra/Aponigricon |
| Sun Sun The Sun is the star at the center of the Solar System. It is almost perfectly spherical and consists of hot plasma interwoven with magnetic fields... |
Perihelion | Aphelion |
| Mercury Mercury (planet) Mercury is the innermost and smallest planet in the Solar System, orbiting the Sun once every 87.969 Earth days. The orbit of Mercury has the highest eccentricity of all the Solar System planets, and it has the smallest axial tilt. It completes three rotations about its axis for every two orbits... |
Perihermion | Apohermion |
| Venus Venus Venus is the second planet from the Sun, orbiting it every 224.7 Earth days. The planet is named after Venus, the Roman goddess of love and beauty. After the Moon, it is the brightest natural object in the night sky, reaching an apparent magnitude of −4.6, bright enough to cast shadows... |
Pericytherion/Pericytherean/Perikrition | Apocytherion/Apocytherean/Apokrition |
| Earth Earth Earth is the third planet from the Sun, and the densest and fifth-largest of the eight planets in the Solar System. It is also the largest of the Solar System's four terrestrial planets... |
Perigee | Apogee |
| Moon Moon The Moon is Earth's only known natural satellite,There are a number of near-Earth asteroids including 3753 Cruithne that are co-orbital with Earth: their orbits bring them close to Earth for periods of time but then alter in the long term . These are quasi-satellites and not true moons. For more... |
Periselene/Pericynthion/Perilune | Aposelene/Apocynthion/Apolune |
| Mars Mars Mars is the fourth planet from the Sun in the Solar System. The planet is named after the Roman god of war, Mars. It is often described as the "Red Planet", as the iron oxide prevalent on its surface gives it a reddish appearance... |
Periareion | Apoareion |
| Jupiter Jupiter Jupiter is the fifth planet from the Sun and the largest planet within the Solar System. It is a gas giant with mass one-thousandth that of the Sun but is two and a half times the mass of all the other planets in our Solar System combined. Jupiter is classified as a gas giant along with Saturn,... |
Perizene/Perijove | Apozene/Apojove |
| Saturn Saturn Saturn is the sixth planet from the Sun and the second largest planet in the Solar System, after Jupiter. Saturn is named after the Roman god Saturn, equated to the Greek Cronus , the Babylonian Ninurta and the Hindu Shani. Saturn's astronomical symbol represents the Roman god's sickle.Saturn,... |
Perikrone/Perisaturnium | Apokrone/Aposaturnium |
| Uranus Uranus Uranus is the seventh planet from the Sun. It has the third-largest planetary radius and fourth-largest planetary mass in the Solar System. It is named after the ancient Greek deity of the sky Uranus , the father of Cronus and grandfather of Zeus... |
Periuranion | Apouranion |
| Neptune Neptune Neptune is the eighth and farthest planet from the Sun in the Solar System. Named for the Roman god of the sea, it is the fourth-largest planet by diameter and the third largest by mass. Neptune is 17 times the mass of Earth and is slightly more massive than its near-twin Uranus, which is 15 times... |
Periposeidion | Apoposeidion |
| Pluto Pluto Pluto, formal designation 134340 Pluto, is the second-most-massive known dwarf planet in the Solar System and the tenth-most-massive body observed directly orbiting the Sun... |
Perihadion | Apohadion |
Since "peri" and "apo" are Greek, it is considered by some purists more correct to use the Greek form for the body, giving forms such as '-zene' for Jupiter and '-krone' for Saturn. The daunting prospect of having to maintain a different word for every orbitable body in the Solar System (and beyond) is the main reason why the generic '-apsis' has become the almost universal norm in cases other than the Sun and Earth.
- In the Moon's case, in practice all three forms are used, albeit very infrequently. The '-cynthion' form (from the moon goddess Artemis' Ancient Greek epithet "Cynthia") is, according to some, reserved for artificial bodies, whilst others reserve '-lune' for an object launched from the Moon and '-cynthion' for an object launched from elsewhere. The '-cynthion' form was the version used in the Apollo Project, following a NASA decision in 1964.
- For Venus, the form '-cytherion' is derived from the commonly used adjective 'cytherean'; the alternate form '-krition' (from Kritias, an older name for AphroditeAphroditeAphrodite is the Greek goddess of love, beauty, pleasure, and procreation.Her Roman equivalent is the goddess .Historically, her cult in Greece was imported from, or influenced by, the cult of Astarte in Phoenicia....
) has also been suggested. - For Jupiter, the '-jove' form is occasionally used by astronomers whilst the '-zene' form is never used, like the other pure Greek forms ('-areion' (Mars), '-hermion' (Mercury), '-krone' (Saturn), '-uranion' (Uranus), '-poseidion' (Neptune) and '-hadion' (Pluto)).
The perihelion and aphelion of the Earth
For the orbit of the Earth around the sun, the time of apsis is often expressed in terms of a time relative to seasons, since this determines the contribution of the elliptical orbit to seasonal variations. The variation of the seasons is primarily controlled by the annual cycle of the elevation angle of the sun, which is a result of the tilt of the axis of the Earth measured from the plane of the eclipticPlane of the ecliptic
The plane of the ecliptic is the plane of the Earth's orbit around the Sun. It is the primary reference plane when describing the position of bodies in the Solar System, with celestial latitude being measured relative to the ecliptic plane. In the course of a year, the Sun's apparent path through...
.
Currently, the annual perihelion happens at about 14 days after the December Solstice, thus on or about January 4. At perihelion, the Earth is about 0.98329 astronomical unit
Astronomical unit
An astronomical unit is a unit of length equal to about or approximately the mean Earth–Sun distance....
s (AU) or 147,098,070 kilometers (about 91,402,500 miles) from the sun. (The eccentricity
Orbital eccentricity
The orbital eccentricity of an astronomical body is the amount by which its orbit deviates from a perfect circle, where 0 is perfectly circular, and 1.0 is a parabola, and no longer a closed orbit...
of the orbit also varies slowly over many millennia.)
Likewise, the annual aphelion currently occurs in early July, about 14 days after the June Solstice. At this time, the distance of the aphelion is currently about 1.01671 AU or 152097700 kilometres (94,509,364.1 mi).
On a very long time scale, the dates of the perihelion and of the aphelion progress through the seasons, and they make one complete cycle in 22,000 to 26,000 years. There is a corresponding movement of the position of the stars as seen from Earth that is called the apsidal precession
Apsidal precession
In celestial mechanics, perihelion precession, apsidal precession or orbital precession is the precession of the orbit of a celestial body. More precisely it is the gradual rotation of the line joining the apsides of an orbit, which are the points of closest and farthest approach...
. (This is not the precession of the axis.)
Astronomers commonly express the timing of perihelion relative to the vernal equinox not in terms of days and hours, but rather as an angle of orbital displacement, the so-called longitude of the periapsis
Longitude of the periapsis
In astrodynamics, the longitude of the periapsis of an orbiting body is the longitude at which the periapsis would occur if the body's inclination were zero. For motion of a planet around the sun, this position could be called longitude of perihelion...
. For the orbit of the Earth, this is called the longitude of perihelion, and in the year 2000 was about 282.895 degrees. By the year 2010, this had advanced by a small fraction of a degree to about 283.067 degrees.
The dates and times of the perihelions and aphelions for several past and future years are listed in the following table:
| Year | Perihelion | Aphelion | ||
|---|---|---|---|---|
| Date | Hour[A] (UT Coordinated Universal Time Coordinated Universal Time is the primary time standard by which the world regulates clocks and time. It is one of several closely related successors to Greenwich Mean Time. Computer servers, online services and other entities that rely on having a universally accepted time use UTC for that purpose... ) |
Date | Hour[A] (UT Coordinated Universal Time Coordinated Universal Time is the primary time standard by which the world regulates clocks and time. It is one of several closely related successors to Greenwich Mean Time. Computer servers, online services and other entities that rely on having a universally accepted time use UTC for that purpose... ) |
|
| January 3 | 20 | July 7 | 00 | |
| January 3 | 00 | July 4 | 08 | |
| January 4 | 15 | July 4 | 02 | |
| January 3 | 00 | July 6 | 12 | |
| January 3 | 19 | July 4 | 15 | |
| January 5 | 01 | July 5 | 04 | |
| January 2 | 05 | July 5 | 15 | |
| January 4 | 12 | July 4 | 00 | |
| January 4 | 07 | July 6 | 20 | |
| January 2 | 23 | July 4 | 16 | |
| January 4 | 14 | July 3 | 20 | |
| January 3 | 06 | July 6 | 17 | |
| January 3 | 05 | July 4 | 22 | |
| January 5 | 08 | July 4 | 12 |
Planetary perihelion and aphelion
The following table shows the distances of the planetPlanet
A planet is a celestial body orbiting a star or stellar remnant that is massive enough to be rounded by its own gravity, is not massive enough to cause thermonuclear fusion, and has cleared its neighbouring region of planetesimals.The term planet is ancient, with ties to history, science,...
s and dwarf planet
Dwarf planet
A dwarf planet, as defined by the International Astronomical Union , is a celestial body orbiting the Sun that is massive enough to be spherical as a result of its own gravity but has not cleared its neighboring region of planetesimals and is not a satellite...
s from the Sun at their perihelion and aphelion.
| Type of body | Body | Distance from Sun at perihelion | Distance from Sun at aphelion |
|---|---|---|---|
| Planet | Mercury | 46001009 km (28,583,772.9 mi) | 69817445 km (43,382,656.9 mi) |
| Venus | 107476170 km (66,782,761.9 mi) | 108942780 km (67,694,073.3 mi) | |
| Earth | 147098291 km (91,402,867.6 mi) | 152098233 km (94,509,695.3 mi) | |
| Mars | 206655215 km (128,409,916.5 mi) | 249232432 km (154,866,238.3 mi) | |
| Jupiter | 740679835 km (460,238,256.1 mi) | 816001807 km (507,041,275.9 mi) | |
| Saturn | 1349823615 km (838,743,593.6 mi) | 1503509229 km (934,239,644.2 mi) | |
| Uranus | 2734998229 km (1,699,453,334.3 mi) | 3006318143 km (1,868,044,131.8 mi) | |
| Neptune | 4459753056 km (2,771,168,961.2 mi) | 4537039826 km (2,819,192,853 mi) | |
| Dwarf planet | Ceres | 380951528 km (236,712,893.5 mi) | 446428973 km (277,398,792.7 mi) |
| Pluto | 4436756954 km (2,756,879,810.4 mi) | 7376124302 km (4,583,322,543.4 mi) | |
| Makemake | 5671928586 km (3,524,381,787.6 mi) | 7894762625 km (4,905,590,257.5 mi) | |
| Haumea | 5157623774 km (3,204,806,799.1 mi) | 7706399149 km (4,788,546,328.9 mi) | |
| Eris | 5765732799 km (3,582,669,168.1 mi) | 14594512904 km (9,068,632,423.2 mi) |
The following chart shows the range of distances of the planets, dwarf planets and Halley's Comet from the Sun.
The images below show the perihelion and aphelion points of the inner and outer planets.
External links
- Apogee - Perigee Photographic Size Comparison, perseus.gr
- Aphelion - Perihelion Photographic Size Comparison, perseus.gr
- Earth's Seasons: Equinoxes, Solstices, Perihelion, and Aphelion, 2000-2020, usno.navy.mil