Dense set
Encyclopedia
In topology
and related areas of mathematics
, a subset
A of a topological space
X is called dense (in X) if any point x in X belongs to A or is a limit point
of A. Informally, for every point in X, the point is either in A or arbitrarily "close" to a member of A - for instance, every real number
is either a rational number
or has one arbitrarily close to it (see Diophantine approximation
).
Formally, a subset A of a topological space X is dense in X if for any point x in X, any neighborhood of x contains at least one point from A. Equivalently, A is dense in X if and only if the only closed subset
of X containing A is X itself. This can also be expressed by saying that the closure
of A is X, or that the interior
of the complement of A is empty.
The density of a topological space X is the least cardinality of a dense subset of X.
s is the following. When the topology of X is given by a metric, the closure
of A in X is the union of A and the set of all limits of sequences of elements in A (its limit points),
Then A is dense in X if
Note that
. If 
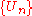is a sequence of dense open
sets in a complete metric space, X, then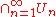
is also dense in X. This fact is one of the equivalent forms of the Baire category theorem
.
s with the usual topology have the rational number
s as a countable
dense subset which shows that the cardinality of a dense subset of a topological space may be strictly smaller than the cardinality of the space itself. The irrational number
s are another dense subset which shows that a topological space may have several disjoint dense subsets.
By the Weierstrass approximation theorem, any given complex-valued
continuous function
defined on a closed interval[ a,b] can be uniformly approximated as closely as desired by a polynomial function. In other words, the polynomial functions are dense in the space C[ a,b] of continuous complex-valued functions on the interval [ a,b] , equipped with the supremum norm.
Every metric space
is dense in its completion.
is dense in itself. For a set X equipped with the discrete topology the whole space is the only dense set. Every non-empty subset of a set X equipped with the trivial topology
is dense, and every topology for which every non-empty subset is dense must be trivial.
Denseness is transitive
: Given three subsets A, B and C of a topological space X with such that A is dense in B and B is dense in C (in the respective subspace topology
) then A is also dense in C.
The image of a dense subset under a surjective
continuous function is again dense. The density of a topological space is a topological invariant.
A topological space with a connected
dense subset is necessarily connected itself.
Continuous function
s into Hausdorff space
s are determined by their values on dense subsets: if two continuous functions into a Hausdorff space
Y agree on a dense subset of X then they agree on all of X.
of A (in X) if every neighbourhood of x also contains a point of A other than x itself, and an isolated point
of A otherwise. A subset without isolated points is said to be dense-in-itself
.
A subset A of a topological space X is called nowhere dense
(in X) if there is no neighborhood in X on which A is dense. Equivalently, a subset of a topological space is nowhere dense if and only if the interior of its closure is empty. The interior of the complement of a nowhere dense set is always dense. The complement of a closed nowhere dense set is a dense open set.
A topological space with a countable dense subset is called separable. A topological space is a Baire space
if and only if the intersection of countably many dense open sets is always dense. A topological space is called resolvable
if it is the union of two disjoint dense subsets. More generally, a topological space is called κ-resolvable if it contains κ pairwise disjoint dense sets.
An embedding
of a topological space X as a dense subset of a compact space
is called a compactification
of X.
A linear operator between topological vector space
s X and Y is said to be densely defined
if its domain
is a dense subset of X and if its range
is contained within Y. See also continuous linear extension.
A topological space X is hyperconnected
if and only if every nonempty open set is dense in X. A topological space is submaximal if and only if every dense subset is open.
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
and related areas of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
A of a topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
X is called dense (in X) if any point x in X belongs to A or is a limit point
Limit point
In mathematics, a limit point of a set S in a topological space X is a point x in X that can be "approximated" by points of S in the sense that every neighbourhood of x with respect to the topology on X also contains a point of S other than x itself. Note that x does not have to be an element of S...
of A. Informally, for every point in X, the point is either in A or arbitrarily "close" to a member of A - for instance, every real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
is either a rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
or has one arbitrarily close to it (see Diophantine approximation
Diophantine approximation
In number theory, the field of Diophantine approximation, named after Diophantus of Alexandria, deals with the approximation of real numbers by rational numbers....
).
Formally, a subset A of a topological space X is dense in X if for any point x in X, any neighborhood of x contains at least one point from A. Equivalently, A is dense in X if and only if the only closed subset
Closed set
In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
of X containing A is X itself. This can also be expressed by saying that the closure
Closure (topology)
In mathematics, the closure of a subset S in a topological space consists of all points in S plus the limit points of S. Intuitively, these are all the points that are "near" S. A point which is in the closure of S is a point of closure of S...
of A is X, or that the interior
Interior (topology)
In mathematics, specifically in topology, the interior of a set S of points of a topological space consists of all points of S that do not belong to the boundary of S. A point that is in the interior of S is an interior point of S....
of the complement of A is empty.
The density of a topological space X is the least cardinality of a dense subset of X.
Density in metric spaces
An alternative definition of dense set in the case of metric spaceMetric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
s is the following. When the topology of X is given by a metric, the closure
Closure (mathematics)
In mathematics, a set is said to be closed under some operation if performance of that operation on members of the set always produces a unique member of the same set. For example, the real numbers are closed under subtraction, but the natural numbers are not: 3 and 8 are both natural numbers, but...
of A in X is the union of A and the set of all limits of sequences of elements in A (its limit points),
Then A is dense in X if
Note that
. If 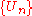is a sequence of dense openOpen set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
sets in a complete metric space, X, then
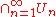is also dense in X. This fact is one of the equivalent forms of the Baire category theoremBaire category theorem
The Baire category theorem is an important tool in general topology and functional analysis. The theorem has two forms, each of which gives sufficient conditions for a topological space to be a Baire space....
.
Examples
The real numberReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s with the usual topology have the rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s as a countable
Countable set
In mathematics, a countable set is a set with the same cardinality as some subset of the set of natural numbers. A set that is not countable is called uncountable. The term was originated by Georg Cantor...
dense subset which shows that the cardinality of a dense subset of a topological space may be strictly smaller than the cardinality of the space itself. The irrational number
Irrational number
In mathematics, an irrational number is any real number that cannot be expressed as a ratio a/b, where a and b are integers, with b non-zero, and is therefore not a rational number....
s are another dense subset which shows that a topological space may have several disjoint dense subsets.
By the Weierstrass approximation theorem, any given complex-valued
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
continuous function
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
defined on a closed interval
Every metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
is dense in its completion.
Properties
Every topological spaceTopological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
is dense in itself. For a set X equipped with the discrete topology the whole space is the only dense set. Every non-empty subset of a set X equipped with the trivial topology
Trivial topology
In topology, a topological space with the trivial topology is one where the only open sets are the empty set and the entire space. Such a space is sometimes called an indiscrete space, and its topology sometimes called an indiscrete topology...
is dense, and every topology for which every non-empty subset is dense must be trivial.
Denseness is transitive
Transitive relation
In mathematics, a binary relation R over a set X is transitive if whenever an element a is related to an element b, and b is in turn related to an element c, then a is also related to c....
: Given three subsets A, B and C of a topological space X with such that A is dense in B and B is dense in C (in the respective subspace topology
Subspace topology
In topology and related areas of mathematics, a subspace of a topological space X is a subset S of X which is equipped with a natural topology induced from that of X called the subspace topology .- Definition :Given a topological space and a subset S of X, the...
) then A is also dense in C.
The image of a dense subset under a surjective
Surjective function
In mathematics, a function f from a set X to a set Y is surjective , or a surjection, if every element y in Y has a corresponding element x in X so that f = y...
continuous function is again dense. The density of a topological space is a topological invariant.
A topological space with a connected
Connected space
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
dense subset is necessarily connected itself.
Continuous function
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
s into Hausdorff space
Hausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
s are determined by their values on dense subsets: if two continuous functions into a Hausdorff space
Hausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
Y agree on a dense subset of X then they agree on all of X.
Related notions
A point x of a subset A of a topological space X is called a limit pointLimit point
In mathematics, a limit point of a set S in a topological space X is a point x in X that can be "approximated" by points of S in the sense that every neighbourhood of x with respect to the topology on X also contains a point of S other than x itself. Note that x does not have to be an element of S...
of A (in X) if every neighbourhood of x also contains a point of A other than x itself, and an isolated point
Isolated point
In topology, a branch of mathematics, a point x of a set S is called an isolated point of S, if there exists a neighborhood of x not containing other points of S.In particular, in a Euclidean space ,...
of A otherwise. A subset without isolated points is said to be dense-in-itself
Dense-in-itself
In mathematics, a subset A of a topological space is said to be dense-in-itself if A contains no isolated points.Every dense-in-itself closed set is perfect. Conversely, every perfect set is dense-in-itself....
.
A subset A of a topological space X is called nowhere dense
Nowhere dense set
In mathematics, a nowhere dense set in a topological space is a set whose closure has empty interior. The order of operations is important. For example, the set of rational numbers, as a subset of R has the property that the closure of the interior is empty, but it is not nowhere dense; in fact it...
(in X) if there is no neighborhood in X on which A is dense. Equivalently, a subset of a topological space is nowhere dense if and only if the interior of its closure is empty. The interior of the complement of a nowhere dense set is always dense. The complement of a closed nowhere dense set is a dense open set.
A topological space with a countable dense subset is called separable. A topological space is a Baire space
Baire space
In mathematics, a Baire space is a topological space which, intuitively speaking, is very large and has "enough" points for certain limit processes. It is named in honor of René-Louis Baire who introduced the concept.- Motivation :...
if and only if the intersection of countably many dense open sets is always dense. A topological space is called resolvable
Resolvable space
In topology, a topological space is said to be resolvable if it is expressible as the union of two disjoint dense subsets. For instance, the real numbers form a resolvable topological space because the rationals and irrationals are disjoint dense subsets...
if it is the union of two disjoint dense subsets. More generally, a topological space is called κ-resolvable if it contains κ pairwise disjoint dense sets.
An embedding
Embedding
In mathematics, an embedding is one instance of some mathematical structure contained within another instance, such as a group that is a subgroup....
of a topological space X as a dense subset of a compact space
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
is called a compactification
Compactification (mathematics)
In mathematics, compactification is the process or result of making a topological space compact. The methods of compactification are various, but each is a way of controlling points from "going off to infinity" by in some way adding "points at infinity" or preventing such an "escape".-An...
of X.
A linear operator between topological vector space
Topological vector space
In mathematics, a topological vector space is one of the basic structures investigated in functional analysis...
s X and Y is said to be densely defined
Densely-defined operator
In mathematics — specifically, in operator theory — a densely defined operator is a type of partially defined function; in a topological sense, it is a linear operator that is defined "almost everywhere"...
if its domain
Domain (mathematics)
In mathematics, the domain of definition or simply the domain of a function is the set of "input" or argument values for which the function is defined...
is a dense subset of X and if its range
Range (mathematics)
In mathematics, the range of a function refers to either the codomain or the image of the function, depending upon usage. This ambiguity is illustrated by the function f that maps real numbers to real numbers with f = x^2. Some books say that range of this function is its codomain, the set of all...
is contained within Y. See also continuous linear extension.
A topological space X is hyperconnected
Hyperconnected space
In mathematics, a hyperconnected space is a topological space X that cannot be written as the union of two proper closed sets. The name irreducible space is preferred in algebraic geometry....
if and only if every nonempty open set is dense in X. A topological space is submaximal if and only if every dense subset is open.