Disjoint union - AbsoluteAstronomy.com

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, the term disjoint union may refer to one of two different concepts:

In set theory
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...

, a disjoint union (or discriminated union) is a modified union
Union (set theory)
In set theory, the union of a collection of sets is the set of all distinct elements in the collection. The union of a collection of sets S_1, S_2, S_3, \dots , S_n\,\! gives a set S_1 \cup S_2 \cup S_3 \cup \dots \cup S_n.- Definition :...

operation that indexes the elements according to which set they originated in; disjoint sets have no element in common.
In probability theory
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...

(or more generally in measure theory
Measure (mathematics)
In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...

), a disjoint union is the usual union of sets that are, however, themselves pairwise disjoint.

Set theory definition

Formally, let {A_i : i ∈ I} be a family of sets

Family of sets

In set theory and related branches of mathematics, a collection F of subsets of a given set S is called a family of subsets of S, or a family of sets over S. More generally, a collection of any sets whatsoever is called a family of sets...

indexed by I. The disjoint union of this family is the set

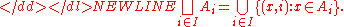
The elements of the disjoint union are ordered pairs (x, i). Here i serves as an auxiliary index that indicates which A_i the element x came from. Each of the sets A_i is canonically embedded in the disjoint union as the set

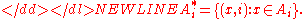
For i ≠ j, the sets A_i* and A_j* are disjoint even if the sets A_i and A_j are not.

In the extreme case where each of the A_i are equal to some fixed set A for each i ∈ I, the disjoint union is the Cartesian product

Cartesian product

In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...

of A and I:

One may occasionally see the notation

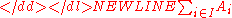
for the disjoint union of a family of sets, or the notation A + B for the disjoint union of two sets. This notation is meant to be suggestive of the fact that the cardinality of the disjoint union is the sum

SUM

SUM can refer to:* The State University of Management* Soccer United Marketing* Society for the Establishment of Useful Manufactures* StartUp-Manager* Software User’s Manual,as from DOD-STD-2 167A, and MIL-STD-498...

of the cardinalities of the terms in the family. Compare this to the notation for the Cartesian product

Cartesian product

of a family of sets.

In the language of category theory

Category theory

Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...

, the disjoint union is the coproduct

Coproduct

In category theory, the coproduct, or categorical sum, is the category-theoretic construction which includes the disjoint union of sets and of topological spaces, the free product of groups, and the direct sum of modules and vector spaces. The coproduct of a family of objects is essentially the...

in the category of sets

Category of sets

In the mathematical field of category theory, the category of sets, denoted as Set, is the category whose objects are sets. The arrows or morphisms between sets A and B are all functions from A to B...

. It therefore satisfies the associated universal property

Universal property

In various branches of mathematics, a useful construction is often viewed as the “most efficient solution” to a certain problem. The definition of a universal property uses the language of category theory to make this notion precise and to study it abstractly.This article gives a general treatment...

. This also means that the disjoint union is the categorical dual of the Cartesian product

Cartesian product

construction. See coproduct

Coproduct

for more details.

For many purposes, the particular choice of auxiliary index is unimportant, and in a simplifying abuse of notation

Abuse of notation

In mathematics, abuse of notation occurs when an author uses a mathematical notation in a way that is not formally correct but that seems likely to simplify the exposition or suggest the correct intuition . Abuse of notation should be contrasted with misuse of notation, which should be avoided...

, the indexed family can be treated simply as a collection of sets. In this case

is referred to as a copy of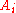

and the notation

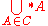is sometimes used.

Probability theory definition

Let C be a collection of pairwise disjoint sets. That is, for all sets A≠B in C, the intersection of these sets is empty: A∩B = ∅. Then the union of all sets in collection C is called the disjoint union of sets:

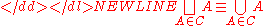
As such, the term “disjoint union” is simply a shorthand for “union of sets which are pairwise disjoint”.

Set theory definition

Probability theory definition

See also