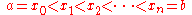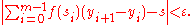
Riemann integral
Encyclopedia
In the branch of mathematics
known as real analysis
, the Riemann integral, created by Bernhard Riemann
, was the first rigorous definition of the integral
of a function
on an interval
. The Riemann integral is unsuitable for many theoretical purposes. For a great many functions and practical applications, the Riemann integral can also be readily evaluated by using the fundamental theorem of calculus
or (approximately) by numerical integration
.
Some of the technical deficiencies in Riemann integration can be remedied by the Riemann–Stieltjes integral, and most of these disappear with the Lebesgue integral.
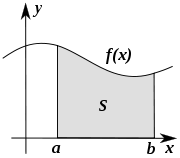
 be a non-negative real-valued function of the interval
be a non-negative real-valued function of the interval 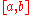 , and let
, and let 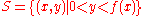 be the region of the plane under the graph of the function
be the region of the plane under the graph of the function  and above the interval
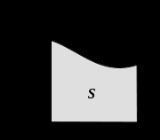
and above the interval 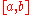 (see the figure on the top right). We are interested in measuring the area of
(see the figure on the top right). We are interested in measuring the area of 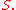 Once we have measured it, we will denote the area by:
Once we have measured it, we will denote the area by:
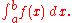
The basic idea of the Riemann integral is to use very simple approximations for the area of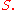 By taking better and better approximations, we can say that "in the limit" we get exactly the area of
By taking better and better approximations, we can say that "in the limit" we get exactly the area of 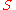 under the curve.
under the curve.
Note that where ƒ can be both positive and negative, the integral corresponds to signed area under the graph of ƒ; that is, the area above the x-axis minus the area below the x-axis.

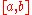 is a finite sequence of numbers of the form
is a finite sequence of numbers of the form
Each [xi , xi+1] is called a subinterval of the partition. The mesh or norm of a partition is defined to be the length of the longest subinterval, that is,

where 0 ≤ i ≤ n − 1. A tagged partition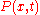 of an interval [a,b] is a partition together with a finite sequence of numbers t0 ,...,tn−1 subject to the conditions that for each i, xi ≤ ti ≤ xi+1. In other words, it is a partition together with a distinguished point of every subinterval. The mesh of a tagged partition is the same as that of an ordinary partition.
of an interval [a,b] is a partition together with a finite sequence of numbers t0 ,...,tn−1 subject to the conditions that for each i, xi ≤ ti ≤ xi+1. In other words, it is a partition together with a distinguished point of every subinterval. The mesh of a tagged partition is the same as that of an ordinary partition.
Suppose that two partitions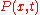 and
and  are both of the interval [a,b]. We say that
are both of the interval [a,b]. We say that 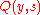 is a refinement of
is a refinement of  if for each integer i with 0 ≤ i ≤ n there exists an integer r(i) such that xi = yr(i) and such that ti = sj for some j with r(i) ≤ j < r(i + 1). Said more simply, a refinement of a tagged partition adds tags to the partition, thus it "refines" the accuracy of the partition.
if for each integer i with 0 ≤ i ≤ n there exists an integer r(i) such that xi = yr(i) and such that ti = sj for some j with r(i) ≤ j < r(i + 1). Said more simply, a refinement of a tagged partition adds tags to the partition, thus it "refines" the accuracy of the partition.
We can define a partial order on the set of all tagged partitions by saying that one tagged partition is greater or equal to another if the former is a refinement of the latter.
 which is defined on the interval
which is defined on the interval  . The Riemann sum
. The Riemann sum
of with respect to the tagged partition
with respect to the tagged partition  together with
together with  is:
is:

Each term in the sum is the product of the value of the function at a given point, and the length of an interval. Consequently, each term represents the area of a rectangle with height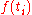 and width
and width  . The Riemann sum is the signed area under all the rectangles.
. The Riemann sum is the signed area under all the rectangles.
One important fact is that the mesh of the partitions must become smaller and smaller, so that in the limit, it is zero. If this were not so, then we would not be getting a good approximation to the function on certain subintervals. In fact, this is enough to define an integral. To be specific, we say that the Riemann integral of ƒ equals s if the following condition holds:

However, there is an unfortunate problem with this definition: it is very difficult to work with. So we will make an alternate definition of the Riemann integral which is easier to work with, then prove that it is the same as the definition we have just made. Our new definition says that the Riemann integral of ƒ equals s if the following condition holds:
Both of these mean that eventually, the Riemann sum of ƒ with respect to any partition gets trapped close to s. Since this is true no matter how close we demand the sums be trapped, we say that the Riemann sums converge to s. These definitions are actually a special case of a more general concept, a net
.
As we stated earlier, these two definitions are equivalent. In other words, s works in the first definition if and only if s works in the second definition. To show that the first definition implies the second, start with an ε, and choose a δ that satisfies the condition. Choose any tagged partition whose mesh is less than δ. Its Riemann sum is within ε of s, and any refinement of this partition will also have mesh less than δ, so the Riemann sum of the refinement will also be within ε of s. To show that the second definition implies the first, it is easiest to use the Darboux integral
. First one shows that the second definition is equivalent to the definition of the Darboux integral; for this see the article on Darboux integration. Now we will show that a Darboux integrable function satisfies the first definition. Fix ε, and choose a partition such that the lower and upper Darboux sums with respect to this partition are within ε/2 of the value s of the Darboux integral. Let r equal the supremum
such that the lower and upper Darboux sums with respect to this partition are within ε/2 of the value s of the Darboux integral. Let r equal the supremum
of |ƒ(x)| on [a,b]. If r = 0, then ƒ is the zero function, which is clearly both Darboux and Riemann integrable with integral zero. Therefore we will assume that r > 0. If m > 1, then we choose δ to be less than both ε/2r(m − 1) and . If m = 1, then we choose δ to be less than one. Choose a tagged partition
. If m = 1, then we choose δ to be less than one. Choose a tagged partition  and
and  . We must show that the Riemann sum is within ε of s.
. We must show that the Riemann sum is within ε of s.
To see this, choose an interval [xi, xi + 1]. If this interval is contained within some [yj, yj + 1], then the value of ƒ(ti) is between mj, the infimum
of ƒ on [yj, yj + 1], and Mj, the supremum of ƒ on [yj, yj + 1]. If all intervals had this property, then this would conclude the proof, because each term in the Riemann sum would be bounded a corresponding term in the Darboux sums, and we chose the Darboux sums to be near s. This is the case when m = 1, so the proof is finished in that case. Therefore we may assume that m > 1. In this case, it is possible that one of the [xi, xi + 1] is not contained in any [yj, yj + 1]. Instead, it may stretch across two of the intervals determined by . (It cannot meet three intervals because δ is assumed to be smaller than the length of any one interval.) In symbols, it may happen that
. (It cannot meet three intervals because δ is assumed to be smaller than the length of any one interval.) In symbols, it may happen that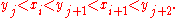
(We may assume that all the inequalities are strict because otherwise we are in the previous case by our assumption on the length of δ.) This can happen at most m − 1 times. To handle this case, we will estimate the difference between the Riemann sum and the Darboux sum by subdividing the partition at yj + 1. The term ƒ(ti)(xi − xi + 1) in the Riemann sum splits into two terms:
at yj + 1. The term ƒ(ti)(xi − xi + 1) in the Riemann sum splits into two terms:

Suppose that ti ∈ [xi, xi + 1]. Then mj ≤ ƒ(ti) ≤ Mj, so this term is bounded by the corresponding term in the Darboux sum for yj. To bound the other term, notice that yj + 1 − xi + 1 is smaller than δ, and δ is chosen to be smaller than ε/2r(m − 1), where r is the supremum of |ƒ(x)|. It follows that the second term is smaller than ε/2(m − 1). Since this happens at most m − 1 times, the total of all the terms which are not bounded by the Darboux sum is at most ε/2. Therefore the distance between the Riemann sum and s is at most ε.
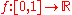 be the function which takes the value 1 at every point. Any Riemann sum of
be the function which takes the value 1 at every point. Any Riemann sum of  on
on 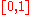 will have the value 1, therefore the Riemann integral of
will have the value 1, therefore the Riemann integral of  on
on  is 1.
is 1.
Let be the indicator function of the rational numbers in
be the indicator function of the rational numbers in 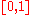 ; that is,
; that is,  takes the value 1 on rational numbers and 0 on irrational numbers. This function does not have a Riemann integral. To prove this, we will show how to construct tagged partitions whose Riemann sums get arbitrarily close to both zero and one.
takes the value 1 on rational numbers and 0 on irrational numbers. This function does not have a Riemann integral. To prove this, we will show how to construct tagged partitions whose Riemann sums get arbitrarily close to both zero and one.
To start, let and
and  be a tagged partition (each
be a tagged partition (each 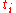 is between
is between 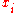 and
and  ). Choose
). Choose  . The
. The 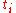 have already been chosen, and we can't change the value of
have already been chosen, and we can't change the value of  at those points. But if we cut the partition into tiny pieces around each
at those points. But if we cut the partition into tiny pieces around each 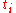 , we can minimize the effect of the
, we can minimize the effect of the 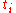 . Then, by carefully choosing the new tags, we can make the value of the Riemann sum turn out to be within
. Then, by carefully choosing the new tags, we can make the value of the Riemann sum turn out to be within  of either zero or one—our choice!
of either zero or one—our choice!
Our first step is to cut up the partition. There are of the
of the 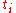 , and we want their total effect to be less than
, and we want their total effect to be less than  . If we confine each of them to an interval of length less than
. If we confine each of them to an interval of length less than 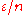 , then the contribution of each
, then the contribution of each 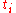 to the Riemann sum will be at least
to the Riemann sum will be at least 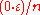 and at most
and at most 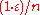 . This makes the total sum at least zero and at most
. This makes the total sum at least zero and at most  . So let
. So let  be a positive number less than
be a positive number less than  . If it happens that two of the
. If it happens that two of the  are within
are within 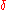 of each other, choose
of each other, choose 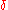 smaller. If it happens that some
smaller. If it happens that some 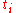 is within
is within 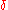 of some
of some  , and
, and 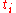 is not equal to
is not equal to 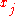 , choose
, choose 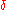 smaller. Since there are only finitely many
smaller. Since there are only finitely many  and
and 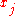 , we can always choose
, we can always choose  sufficiently small.
sufficiently small.
Now we add two cuts to the partition for each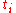 . One of the cuts will be at
. One of the cuts will be at 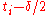 , and the other will be at
, and the other will be at 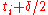 . If one of these leaves the interval
. If one of these leaves the interval 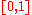 , then we leave it out.
, then we leave it out. 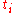 will be the tag corresponding to the subinterval
will be the tag corresponding to the subinterval 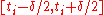 . If
. If 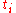 is directly on top of one of the
is directly on top of one of the 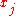 , then we let
, then we let 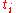 be the tag for both
be the tag for both  and
and  . We still have to choose tags for the other subintervals. We will choose them in two different ways. The first way is to always choose a rational point, so that the Riemann sum is as large as possible. This will make the value of the Riemann sum at least
. We still have to choose tags for the other subintervals. We will choose them in two different ways. The first way is to always choose a rational point, so that the Riemann sum is as large as possible. This will make the value of the Riemann sum at least  . The second way is to always choose an irrational point, so that the Riemann sum is as small as possible. This will make the value of the Riemann sum at most
. The second way is to always choose an irrational point, so that the Riemann sum is as small as possible. This will make the value of the Riemann sum at most  .
.
Since we started from an arbitrary partition and ended up as close as we wanted to either zero or one, it is false to say that we are eventually trapped near some number , so this function is not Riemann integrable. However, it is Lebesgue integrable. In the Lebesgue sense its integral is zero, since the function is zero almost everywhere
, so this function is not Riemann integrable. However, it is Lebesgue integrable. In the Lebesgue sense its integral is zero, since the function is zero almost everywhere
. But this is a fact that is beyond the reach of the Riemann integral.
There are even worse examples. is equivalent (that is, equal almost everywhere) to a Riemann integrable function, but there are non-Riemann integrable bounded functions which are not equivalent to any Riemann integrable function. For example, let C be the Smith–Volterra–Cantor set, and let IC be its indicator function. Because C is not Jordan measurable
is equivalent (that is, equal almost everywhere) to a Riemann integrable function, but there are non-Riemann integrable bounded functions which are not equivalent to any Riemann integrable function. For example, let C be the Smith–Volterra–Cantor set, and let IC be its indicator function. Because C is not Jordan measurable
, IC is not Riemann integrable. Moreover, no function g equivalent to IC is Riemann integrable: g, like IC, must be zero on a dense set, so as in the previous example, any Riemann sum of g has a refinement which is within ε of 0 for any positive number ε. But if the Riemann integral of g exists, then it must equal the Lebesgue integral of IC, which is 1/2. Therefore g is not Riemann integrable.
. This is because the Darboux integral is technically simpler and because a function is Riemann-integrable if and only if it is Darboux-integrable.
Some calculus books do not use general tagged partitions, but limit themselves to specific types of tagged partitions. If the type of partition is limited too much, some non-integrable functions may appear to be integrable.
One popular restriction is the use of "left-hand" and "right-hand" Riemann sums. In a left-hand Riemann sum,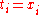 for all
for all 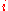 , and in a right-hand Riemann sum,
, and in a right-hand Riemann sum, 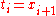 for all
for all 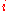 . Alone this restriction does not impose a problem: we can refine any partition in a way that makes it a left-hand or right-hand sum by subdividing it at each
. Alone this restriction does not impose a problem: we can refine any partition in a way that makes it a left-hand or right-hand sum by subdividing it at each 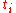 . In more formal language, the set of all left-hand Riemann sums and the set of all right-hand Riemann sums is cofinal
. In more formal language, the set of all left-hand Riemann sums and the set of all right-hand Riemann sums is cofinal
in the set of all tagged partitions.
Another popular restriction is the use of regular subdivisions of an interval. For example, the th regular subdivision of
th regular subdivision of 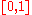 consists of the intervals
consists of the intervals 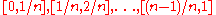 . Again, alone this restriction does not impose a problem, but the reasoning required to see this fact is more difficult than in the case of left-hand and right-hand Riemann sums.
. Again, alone this restriction does not impose a problem, but the reasoning required to see this fact is more difficult than in the case of left-hand and right-hand Riemann sums.
However, combining these restrictions, so that one uses only left-hand or right-hand Riemann sums on regularly divided intervals, is dangerous. If a function is known in advance to be Riemann integrable, then this technique will give the correct value of the integral. But under these conditions the indicator function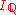 will appear to be integrable on
will appear to be integrable on  with integral equal to one: Every endpoint of every subinterval will be a rational number, so the function will always be evaluated at rational numbers, and hence it will appear to always equal one. The problem with this definition becomes apparent when we try to split the integral into two pieces. The following equation ought to hold:
with integral equal to one: Every endpoint of every subinterval will be a rational number, so the function will always be evaluated at rational numbers, and hence it will appear to always equal one. The problem with this definition becomes apparent when we try to split the integral into two pieces. The following equation ought to hold:

If we use regular subdivisions and left-hand or right-hand Riemann sums, then the two terms on the left are equal to zero, since every endpoint except 0 and 1 will be irrational, but as we have seen the term on the right will equal 1.
As defined above, the Riemann integral avoids this problem by refusing to integrate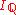 . The Lebesgue integral is defined in such a way that all these integrals are 0.
. The Lebesgue integral is defined in such a way that all these integrals are 0.
 and
and  are Riemann-integrable on
are Riemann-integrable on  and
and  and
and 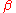 are constants, then
are constants, then
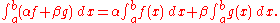
Because the Riemann integral of a function is a number, this makes the Riemann integral a linear functional on the vector space of Riemann-integrable functions.
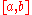 is Riemann integrable if and only if it is bounded
is Riemann integrable if and only if it is bounded
and continuous
almost everywhere
(the set of its points of discontinuity has measure zero, in the sense of Lebesgue measure
). This is known as the or Lebesgue's criterion for Riemann integrability. Note that this should not be confused with the notion of the Lebesgue integral of a function existing; the result is due to Lebesgue, and uses the notion of measure zero, but does not refer to or use Lebesgue measure more generally, or the Lebesgue integral.
The integrability condition can be proven in various ways, one of which is sketched below.
In particular, a countable set
has measure zero, and thus a bounded function (on a compact interval) with only finitely many or countably infinitely many discontinuities is Riemann integrable.
An indicator function of a bounded set is Riemann-integrable if and only if the set is Jordan measurable
.
If a real-valued function is monotone on the interval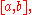 it is Riemann-integrable, since its set of discontinuities is denumerable, and therefore of Lebesgue measure zero.
it is Riemann-integrable, since its set of discontinuities is denumerable, and therefore of Lebesgue measure zero.
If a real-valued function on is Riemann-integrable, it is Lebesgue-integrable. That is, Riemann-integrability is a stronger (meaning more difficult to satisfy) condition than Lebesgue-integrability.
is Riemann-integrable, it is Lebesgue-integrable. That is, Riemann-integrability is a stronger (meaning more difficult to satisfy) condition than Lebesgue-integrability.
If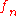 is a uniformly convergent sequence on
is a uniformly convergent sequence on 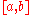 with limit
with limit  , then Riemann integrability of all
, then Riemann integrability of all 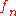 implies Riemann integrability of
implies Riemann integrability of  , and
, and

However, the Lebesgue monotone convergence theorem (on a monotone pointwise limit) does not hold.
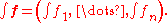
In particular, since the complex numbers are a real vector space
, this allows the integration of complex valued functions.
The Riemann integral is only defined on bounded intervals, and it does not extend well to unbounded intervals. The simplest possible extension is to define such an integral as a limit, in other words, as an improper integral
. We could set: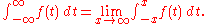
Unfortunately, this does not work well. Translation invariance, the fact that the Riemann integral of the function should not change if we move the function left or right, is lost. For example, let for all , and for all then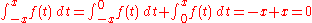
for all x. But if we shift ƒ(x) to the right by one unit to get ƒ(x−1), we get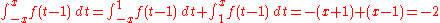
for all Since this is unacceptable, we could try the definition: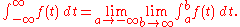
Then if we attempt to integrate the function ƒ above, we get +∞, because we take the limit first. If we reverse the order of the limits, then we get −∞.
This is also unacceptable, so we could require that the integral exists and gives the same value regardless of the order. Even this does not give us what we want, because the Riemann integral no longer commutes with uniform limits. For example, let on (0,n) and 0 everywhere else. For all n we have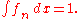
But ƒn converges uniformly to zero, so the integral of lim(ƒn) is zero. Consequently
Even though this is the correct value, it shows that the most important criterion for exchanging limits and (proper) integrals is false for improper integrals. This makes the Riemann integral unworkable in applications.
A better route is to abandon the Riemann integral for the Lebesgue integral. The definition of the Lebesgue integral is not obviously a generalization of the Riemann integral, but it is not hard to prove that every Riemann-integrable function is Lebesgue-integrable and that the values of the two integrals agree whenever they are both defined. Moreover, a function ƒ defined on a bounded interval is Riemann-integrable if and only if it is bounded and the set of points where ƒ is discontinuous has Lebesgue measure zero.
An integral which is in fact a direct generalization of the Riemann integral is the Henstock–Kurzweil integral.
Another way of generalizing the Riemann integral is to replace the factors in the definition of a Riemann sum by something else; roughly speaking, this gives the interval of integration a different notion of length. This is the approach taken by the Riemann–Stieltjes integral.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
known as real analysis
Real analysis
Real analysis, is a branch of mathematical analysis dealing with the set of real numbers and functions of a real variable. In particular, it deals with the analytic properties of real functions and sequences, including convergence and limits of sequences of real numbers, the calculus of the real...
, the Riemann integral, created by Bernhard Riemann
Bernhard Riemann
Georg Friedrich Bernhard Riemann was an influential German mathematician who made lasting contributions to analysis and differential geometry, some of them enabling the later development of general relativity....
, was the first rigorous definition of the integral
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
of a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
on an interval
Interval (mathematics)
In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...
. The Riemann integral is unsuitable for many theoretical purposes. For a great many functions and practical applications, the Riemann integral can also be readily evaluated by using the fundamental theorem of calculus
Fundamental theorem of calculus
The first part of the theorem, sometimes called the first fundamental theorem of calculus, shows that an indefinite integration can be reversed by a differentiation...
or (approximately) by numerical integration
Numerical integration
In numerical analysis, numerical integration constitutes a broad family of algorithms for calculating the numerical value of a definite integral, and by extension, the term is also sometimes used to describe the numerical solution of differential equations. This article focuses on calculation of...
.
Some of the technical deficiencies in Riemann integration can be remedied by the Riemann–Stieltjes integral, and most of these disappear with the Lebesgue integral.

Overview
Let be a non-negative real-valued function of the interval
be a non-negative real-valued function of the interval 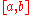 , and let
, and let 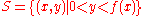 be the region of the plane under the graph of the function
be the region of the plane under the graph of the function  and above the interval
and above the interval 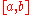 (see the figure on the top right). We are interested in measuring the area of
(see the figure on the top right). We are interested in measuring the area of 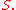 Once we have measured it, we will denote the area by:
Once we have measured it, we will denote the area by: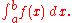
The basic idea of the Riemann integral is to use very simple approximations for the area of
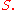 By taking better and better approximations, we can say that "in the limit" we get exactly the area of
By taking better and better approximations, we can say that "in the limit" we get exactly the area of 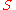 under the curve.
under the curve.Note that where ƒ can be both positive and negative, the integral corresponds to signed area under the graph of ƒ; that is, the area above the x-axis minus the area below the x-axis.

Partitions of an interval
A partition of an intervalPartition of an interval
In mathematics, a partition, P of an interval [a, b] on the real line is a finite sequence of the formIn mathematics, a partition, P of an interval [a, b] on the real line is a finite sequence of the form...
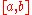 is a finite sequence of numbers of the form
is a finite sequence of numbers of the formEach [xi , xi+1] is called a subinterval of the partition. The mesh or norm of a partition is defined to be the length of the longest subinterval, that is,

where 0 ≤ i ≤ n − 1. A tagged partition
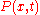 of an interval [a,b] is a partition together with a finite sequence of numbers t0 ,...,tn−1 subject to the conditions that for each i, xi ≤ ti ≤ xi+1. In other words, it is a partition together with a distinguished point of every subinterval. The mesh of a tagged partition is the same as that of an ordinary partition.
of an interval [a,b] is a partition together with a finite sequence of numbers t0 ,...,tn−1 subject to the conditions that for each i, xi ≤ ti ≤ xi+1. In other words, it is a partition together with a distinguished point of every subinterval. The mesh of a tagged partition is the same as that of an ordinary partition.Suppose that two partitions
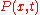 and
and  are both of the interval [a,b]. We say that
are both of the interval [a,b]. We say that 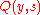 is a refinement of
is a refinement of  if for each integer i with 0 ≤ i ≤ n there exists an integer r(i) such that xi = yr(i) and such that ti = sj for some j with r(i) ≤ j < r(i + 1). Said more simply, a refinement of a tagged partition adds tags to the partition, thus it "refines" the accuracy of the partition.
if for each integer i with 0 ≤ i ≤ n there exists an integer r(i) such that xi = yr(i) and such that ti = sj for some j with r(i) ≤ j < r(i + 1). Said more simply, a refinement of a tagged partition adds tags to the partition, thus it "refines" the accuracy of the partition.We can define a partial order on the set of all tagged partitions by saying that one tagged partition is greater or equal to another if the former is a refinement of the latter.
Riemann sums
Choose a real-valued function which is defined on the interval
which is defined on the interval  . The Riemann sum
. The Riemann sumRiemann sum
In mathematics, a Riemann sum is a method for approximating the total area underneath a curve on a graph, otherwise known as an integral. It mayalso be used to define the integration operation. The method was named after German mathematician Bernhard Riemann....
of
 with respect to the tagged partition
with respect to the tagged partition  together with
together with  is:
is:
Each term in the sum is the product of the value of the function at a given point, and the length of an interval. Consequently, each term represents the area of a rectangle with height
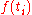 and width
and width  . The Riemann sum is the signed area under all the rectangles.
. The Riemann sum is the signed area under all the rectangles.Riemann integral
Loosely speaking, the Riemann integral is the limit of the Riemann sums of a function as the partitions get finer. If the limit exists then the function is said to be integrable (or more specifically Riemann-integrable). The Riemann sum can be made as close as desired to the Riemann integral by making the partition fine enough.One important fact is that the mesh of the partitions must become smaller and smaller, so that in the limit, it is zero. If this were not so, then we would not be getting a good approximation to the function on certain subintervals. In fact, this is enough to define an integral. To be specific, we say that the Riemann integral of ƒ equals s if the following condition holds:
- For all ε > 0, there exists δ > 0 such that for any tagged partition
 and
and  whose mesh is less than δ, we have
whose mesh is less than δ, we have

However, there is an unfortunate problem with this definition: it is very difficult to work with. So we will make an alternate definition of the Riemann integral which is easier to work with, then prove that it is the same as the definition we have just made. Our new definition says that the Riemann integral of ƒ equals s if the following condition holds:
- For all ε > 0, there exists a tagged partition
 and
and  such that for any refinement
such that for any refinement  and
and  of
of  and
and  , we have
, we have
Both of these mean that eventually, the Riemann sum of ƒ with respect to any partition gets trapped close to s. Since this is true no matter how close we demand the sums be trapped, we say that the Riemann sums converge to s. These definitions are actually a special case of a more general concept, a net
Net (mathematics)
In mathematics, more specifically in general topology and related branches, a net or Moore–Smith sequence is a generalization of the notion of a sequence. In essence, a sequence is a function with domain the natural numbers, and in the context of topology, the range of this function is...
.
As we stated earlier, these two definitions are equivalent. In other words, s works in the first definition if and only if s works in the second definition. To show that the first definition implies the second, start with an ε, and choose a δ that satisfies the condition. Choose any tagged partition whose mesh is less than δ. Its Riemann sum is within ε of s, and any refinement of this partition will also have mesh less than δ, so the Riemann sum of the refinement will also be within ε of s. To show that the second definition implies the first, it is easiest to use the Darboux integral
Darboux integral
In real analysis, a branch of mathematics, the Darboux integral or Darboux sum is one possible definition of the integral of a function. Darboux integrals are equivalent to Riemann integrals, meaning that a function is Darboux-integrable if and only if it is Riemann-integrable, and the values of...
. First one shows that the second definition is equivalent to the definition of the Darboux integral; for this see the article on Darboux integration. Now we will show that a Darboux integrable function satisfies the first definition. Fix ε, and choose a partition
 such that the lower and upper Darboux sums with respect to this partition are within ε/2 of the value s of the Darboux integral. Let r equal the supremum
such that the lower and upper Darboux sums with respect to this partition are within ε/2 of the value s of the Darboux integral. Let r equal the supremumSupremum
In mathematics, given a subset S of a totally or partially ordered set T, the supremum of S, if it exists, is the least element of T that is greater than or equal to every element of S. Consequently, the supremum is also referred to as the least upper bound . If the supremum exists, it is unique...
of |ƒ(x)| on [a,b]. If r = 0, then ƒ is the zero function, which is clearly both Darboux and Riemann integrable with integral zero. Therefore we will assume that r > 0. If m > 1, then we choose δ to be less than both ε/2r(m − 1) and
 . If m = 1, then we choose δ to be less than one. Choose a tagged partition
. If m = 1, then we choose δ to be less than one. Choose a tagged partition  and
and  . We must show that the Riemann sum is within ε of s.
. We must show that the Riemann sum is within ε of s.To see this, choose an interval [xi, xi + 1]. If this interval is contained within some [yj, yj + 1], then the value of ƒ(ti) is between mj, the infimum
Infimum
In mathematics, the infimum of a subset S of some partially ordered set T is the greatest element of T that is less than or equal to all elements of S. Consequently the term greatest lower bound is also commonly used...
of ƒ on [yj, yj + 1], and Mj, the supremum of ƒ on [yj, yj + 1]. If all intervals had this property, then this would conclude the proof, because each term in the Riemann sum would be bounded a corresponding term in the Darboux sums, and we chose the Darboux sums to be near s. This is the case when m = 1, so the proof is finished in that case. Therefore we may assume that m > 1. In this case, it is possible that one of the [xi, xi + 1] is not contained in any [yj, yj + 1]. Instead, it may stretch across two of the intervals determined by
 . (It cannot meet three intervals because δ is assumed to be smaller than the length of any one interval.) In symbols, it may happen that
. (It cannot meet three intervals because δ is assumed to be smaller than the length of any one interval.) In symbols, it may happen that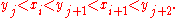
(We may assume that all the inequalities are strict because otherwise we are in the previous case by our assumption on the length of δ.) This can happen at most m − 1 times. To handle this case, we will estimate the difference between the Riemann sum and the Darboux sum by subdividing the partition
 at yj + 1. The term ƒ(ti)(xi − xi + 1) in the Riemann sum splits into two terms:
at yj + 1. The term ƒ(ti)(xi − xi + 1) in the Riemann sum splits into two terms:
Suppose that ti ∈ [xi, xi + 1]. Then mj ≤ ƒ(ti) ≤ Mj, so this term is bounded by the corresponding term in the Darboux sum for yj. To bound the other term, notice that yj + 1 − xi + 1 is smaller than δ, and δ is chosen to be smaller than ε/2r(m − 1), where r is the supremum of |ƒ(x)|. It follows that the second term is smaller than ε/2(m − 1). Since this happens at most m − 1 times, the total of all the terms which are not bounded by the Darboux sum is at most ε/2. Therefore the distance between the Riemann sum and s is at most ε.
Examples
Let be the function which takes the value 1 at every point. Any Riemann sum of
be the function which takes the value 1 at every point. Any Riemann sum of  on
on  will have the value 1, therefore the Riemann integral of
will have the value 1, therefore the Riemann integral of  on
on  is 1.
is 1.Let
 be the indicator function of the rational numbers in
be the indicator function of the rational numbers in 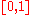 ; that is,
; that is,  takes the value 1 on rational numbers and 0 on irrational numbers. This function does not have a Riemann integral. To prove this, we will show how to construct tagged partitions whose Riemann sums get arbitrarily close to both zero and one.
takes the value 1 on rational numbers and 0 on irrational numbers. This function does not have a Riemann integral. To prove this, we will show how to construct tagged partitions whose Riemann sums get arbitrarily close to both zero and one.To start, let
 and
and  be a tagged partition (each
be a tagged partition (each 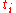 is between
is between 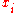 and
and  ). Choose
). Choose  . The
. The 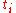 have already been chosen, and we can't change the value of
have already been chosen, and we can't change the value of  at those points. But if we cut the partition into tiny pieces around each
at those points. But if we cut the partition into tiny pieces around each 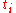 , we can minimize the effect of the
, we can minimize the effect of the 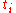 . Then, by carefully choosing the new tags, we can make the value of the Riemann sum turn out to be within
. Then, by carefully choosing the new tags, we can make the value of the Riemann sum turn out to be within  of either zero or one—our choice!
of either zero or one—our choice!Our first step is to cut up the partition. There are
 of the
of the 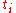 , and we want their total effect to be less than
, and we want their total effect to be less than  . If we confine each of them to an interval of length less than
. If we confine each of them to an interval of length less than 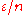 , then the contribution of each
, then the contribution of each 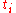 to the Riemann sum will be at least
to the Riemann sum will be at least 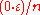 and at most
and at most 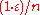 . This makes the total sum at least zero and at most
. This makes the total sum at least zero and at most  . So let
. So let  be a positive number less than
be a positive number less than  . If it happens that two of the
. If it happens that two of the  are within
are within 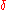 of each other, choose
of each other, choose 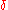 smaller. If it happens that some
smaller. If it happens that some 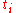 is within
is within 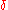 of some
of some  , and
, and 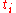 is not equal to
is not equal to 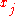 , choose
, choose 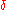 smaller. Since there are only finitely many
smaller. Since there are only finitely many  and
and 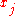 , we can always choose
, we can always choose  sufficiently small.
sufficiently small.Now we add two cuts to the partition for each
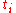 . One of the cuts will be at
. One of the cuts will be at 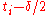 , and the other will be at
, and the other will be at 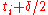 . If one of these leaves the interval
. If one of these leaves the interval 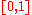 , then we leave it out.
, then we leave it out. 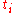 will be the tag corresponding to the subinterval
will be the tag corresponding to the subinterval 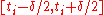 . If
. If 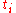 is directly on top of one of the
is directly on top of one of the 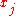 , then we let
, then we let 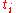 be the tag for both
be the tag for both  and
and  . We still have to choose tags for the other subintervals. We will choose them in two different ways. The first way is to always choose a rational point, so that the Riemann sum is as large as possible. This will make the value of the Riemann sum at least
. We still have to choose tags for the other subintervals. We will choose them in two different ways. The first way is to always choose a rational point, so that the Riemann sum is as large as possible. This will make the value of the Riemann sum at least  . The second way is to always choose an irrational point, so that the Riemann sum is as small as possible. This will make the value of the Riemann sum at most
. The second way is to always choose an irrational point, so that the Riemann sum is as small as possible. This will make the value of the Riemann sum at most  .
.Since we started from an arbitrary partition and ended up as close as we wanted to either zero or one, it is false to say that we are eventually trapped near some number
 , so this function is not Riemann integrable. However, it is Lebesgue integrable. In the Lebesgue sense its integral is zero, since the function is zero almost everywhere
, so this function is not Riemann integrable. However, it is Lebesgue integrable. In the Lebesgue sense its integral is zero, since the function is zero almost everywhereAlmost everywhere
In measure theory , a property holds almost everywhere if the set of elements for which the property does not hold is a null set, that is, a set of measure zero . In cases where the measure is not complete, it is sufficient that the set is contained within a set of measure zero...
. But this is a fact that is beyond the reach of the Riemann integral.
There are even worse examples.
 is equivalent (that is, equal almost everywhere) to a Riemann integrable function, but there are non-Riemann integrable bounded functions which are not equivalent to any Riemann integrable function. For example, let C be the Smith–Volterra–Cantor set, and let IC be its indicator function. Because C is not Jordan measurable
is equivalent (that is, equal almost everywhere) to a Riemann integrable function, but there are non-Riemann integrable bounded functions which are not equivalent to any Riemann integrable function. For example, let C be the Smith–Volterra–Cantor set, and let IC be its indicator function. Because C is not Jordan measurableJordan measure
In mathematics, the Peano–Jordan measure is an extension of the notion of size to shapes more complicated than, for example, a triangle, disk, or parallelepiped....
, IC is not Riemann integrable. Moreover, no function g equivalent to IC is Riemann integrable: g, like IC, must be zero on a dense set, so as in the previous example, any Riemann sum of g has a refinement which is within ε of 0 for any positive number ε. But if the Riemann integral of g exists, then it must equal the Lebesgue integral of IC, which is 1/2. Therefore g is not Riemann integrable.
Similar concepts
It is popular to define the Riemann integral as the Darboux integralDarboux integral
In real analysis, a branch of mathematics, the Darboux integral or Darboux sum is one possible definition of the integral of a function. Darboux integrals are equivalent to Riemann integrals, meaning that a function is Darboux-integrable if and only if it is Riemann-integrable, and the values of...
. This is because the Darboux integral is technically simpler and because a function is Riemann-integrable if and only if it is Darboux-integrable.
Some calculus books do not use general tagged partitions, but limit themselves to specific types of tagged partitions. If the type of partition is limited too much, some non-integrable functions may appear to be integrable.
One popular restriction is the use of "left-hand" and "right-hand" Riemann sums. In a left-hand Riemann sum,
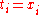 for all
for all 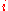 , and in a right-hand Riemann sum,
, and in a right-hand Riemann sum, 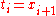 for all
for all 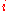 . Alone this restriction does not impose a problem: we can refine any partition in a way that makes it a left-hand or right-hand sum by subdividing it at each
. Alone this restriction does not impose a problem: we can refine any partition in a way that makes it a left-hand or right-hand sum by subdividing it at each 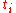 . In more formal language, the set of all left-hand Riemann sums and the set of all right-hand Riemann sums is cofinal
. In more formal language, the set of all left-hand Riemann sums and the set of all right-hand Riemann sums is cofinalCofinal (mathematics)
In mathematics, let A be a set and let ≤ be a binary relation on A. Then a subset B of A is said to be cofinal if it satisfies the following condition:This definition is most commonly applied when A is a partially ordered set or directed set under the relation ≤. Also, the notion of cofinal...
in the set of all tagged partitions.
Another popular restriction is the use of regular subdivisions of an interval. For example, the
 th regular subdivision of
th regular subdivision of 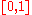 consists of the intervals
consists of the intervals 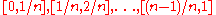 . Again, alone this restriction does not impose a problem, but the reasoning required to see this fact is more difficult than in the case of left-hand and right-hand Riemann sums.
. Again, alone this restriction does not impose a problem, but the reasoning required to see this fact is more difficult than in the case of left-hand and right-hand Riemann sums.However, combining these restrictions, so that one uses only left-hand or right-hand Riemann sums on regularly divided intervals, is dangerous. If a function is known in advance to be Riemann integrable, then this technique will give the correct value of the integral. But under these conditions the indicator function
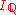 will appear to be integrable on
will appear to be integrable on  with integral equal to one: Every endpoint of every subinterval will be a rational number, so the function will always be evaluated at rational numbers, and hence it will appear to always equal one. The problem with this definition becomes apparent when we try to split the integral into two pieces. The following equation ought to hold:
with integral equal to one: Every endpoint of every subinterval will be a rational number, so the function will always be evaluated at rational numbers, and hence it will appear to always equal one. The problem with this definition becomes apparent when we try to split the integral into two pieces. The following equation ought to hold:
If we use regular subdivisions and left-hand or right-hand Riemann sums, then the two terms on the left are equal to zero, since every endpoint except 0 and 1 will be irrational, but as we have seen the term on the right will equal 1.
As defined above, the Riemann integral avoids this problem by refusing to integrate
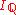 . The Lebesgue integral is defined in such a way that all these integrals are 0.
. The Lebesgue integral is defined in such a way that all these integrals are 0.Linearity
The Riemann integral is a linear transformation; that is, if and
and  are Riemann-integrable on
are Riemann-integrable on  and
and  and
and 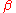 are constants, then
are constants, then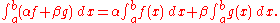
Because the Riemann integral of a function is a number, this makes the Riemann integral a linear functional on the vector space of Riemann-integrable functions.
Integrability
A function on a compact interval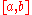 is Riemann integrable if and only if it is bounded
is Riemann integrable if and only if it is boundedBoundedness
Boundedness or bounded may refer to:*Bounded set, a set that is finite in some sense*Bounded function, a function or sequence whose possible values form a bounded set...
and continuous
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
almost everywhere
Almost everywhere
In measure theory , a property holds almost everywhere if the set of elements for which the property does not hold is a null set, that is, a set of measure zero . In cases where the measure is not complete, it is sufficient that the set is contained within a set of measure zero...
(the set of its points of discontinuity has measure zero, in the sense of Lebesgue measure
Lebesgue measure
In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
). This is known as the or Lebesgue's criterion for Riemann integrability. Note that this should not be confused with the notion of the Lebesgue integral of a function existing; the result is due to Lebesgue, and uses the notion of measure zero, but does not refer to or use Lebesgue measure more generally, or the Lebesgue integral.
The integrability condition can be proven in various ways, one of which is sketched below.
| Proof |
|---|
| The proof is easiest using the Darboux integral Darboux integral In real analysis, a branch of mathematics, the Darboux integral or Darboux sum is one possible definition of the integral of a function. Darboux integrals are equivalent to Riemann integrals, meaning that a function is Darboux-integrable if and only if it is Riemann-integrable, and the values of... definition of integrability (formally, the Riemann condition for integrability) – a function is Riemann integrable if and only if the upper and lower sums can be made arbitrarily close by choosing an appropriate partition. One direction is very brief by using the oscillation Oscillation (mathematics) In mathematics, oscillation is the behaviour of a sequence of real numbers or a real-valued function, which does not converge, but also does not diverge to +∞ or −∞; that is, oscillation is the failure to have a limit, and is also a quantitative measure for that.Oscillation is defined as the... definition of continuity: if f is discontinuous on a set of positive measure, then for some ε, f has oscillation at least ε on a set Xε of positive measure 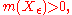 so the upper and lower integrals of f differ by at least so the upper and lower integrals of f differ by at least 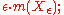 this is where oscillation is used. this is where oscillation is used.The converse direction is straightforward but longer. Conversely, if f is continuous almost everywhere, then for any partition of the interval 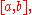 first divide the partition into two sets of intervals, C and D, with D containing all discontinuous points and C containing the rest. Intuitively, the width of D can be made arbitrarily small, while the height of C can be made arbitrarily small. Formally, for any ε, one can choose a subpartition D′ such that discontinuities are contained in intervals of total length at most ε; then the lower sum and upper sum on D′ differ by at most first divide the partition into two sets of intervals, C and D, with D containing all discontinuous points and C containing the rest. Intuitively, the width of D can be made arbitrarily small, while the height of C can be made arbitrarily small. Formally, for any ε, one can choose a subpartition D′ such that discontinuities are contained in intervals of total length at most ε; then the lower sum and upper sum on D′ differ by at most 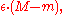 where m and M are the infimum and supremum of f; this is where boundedness is used, and implicitly the equivalence of Jordan content zero and Lebesgue measure zero on a compact set (hence a finite partition can be used). On the rest (C′), the function is continuous on a compact interval, hence uniformly continuous, so a subpartition can be chosen such that on each subinterval, the function varies by at most ε, so the lower and upper sums differ by at most where m and M are the infimum and supremum of f; this is where boundedness is used, and implicitly the equivalence of Jordan content zero and Lebesgue measure zero on a compact set (hence a finite partition can be used). On the rest (C′), the function is continuous on a compact interval, hence uniformly continuous, so a subpartition can be chosen such that on each subinterval, the function varies by at most ε, so the lower and upper sums differ by at most  (this is where compactness is used). The total difference is thus bounded by (this is where compactness is used). The total difference is thus bounded by  which is a constant times ε, and hence can be made arbitrarily small, thus the function is Riemann integrable. which is a constant times ε, and hence can be made arbitrarily small, thus the function is Riemann integrable. |
In particular, a countable set
Countable set
In mathematics, a countable set is a set with the same cardinality as some subset of the set of natural numbers. A set that is not countable is called uncountable. The term was originated by Georg Cantor...
has measure zero, and thus a bounded function (on a compact interval) with only finitely many or countably infinitely many discontinuities is Riemann integrable.
An indicator function of a bounded set is Riemann-integrable if and only if the set is Jordan measurable
Jordan measure
In mathematics, the Peano–Jordan measure is an extension of the notion of size to shapes more complicated than, for example, a triangle, disk, or parallelepiped....
.
If a real-valued function is monotone on the interval
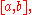 it is Riemann-integrable, since its set of discontinuities is denumerable, and therefore of Lebesgue measure zero.
it is Riemann-integrable, since its set of discontinuities is denumerable, and therefore of Lebesgue measure zero.If a real-valued function on
 is Riemann-integrable, it is Lebesgue-integrable. That is, Riemann-integrability is a stronger (meaning more difficult to satisfy) condition than Lebesgue-integrability.
is Riemann-integrable, it is Lebesgue-integrable. That is, Riemann-integrability is a stronger (meaning more difficult to satisfy) condition than Lebesgue-integrability.If
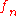 is a uniformly convergent sequence on
is a uniformly convergent sequence on 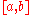 with limit
with limit  , then Riemann integrability of all
, then Riemann integrability of all 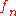 implies Riemann integrability of
implies Riemann integrability of  , and
, and
However, the Lebesgue monotone convergence theorem (on a monotone pointwise limit) does not hold.
Generalizations
It is easy to extend the Riemann integral to functions with values in the Euclidean vector space Rn for any n. The integral is defined by linearity; in other words, if then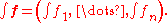
In particular, since the complex numbers are a real vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
, this allows the integration of complex valued functions.
The Riemann integral is only defined on bounded intervals, and it does not extend well to unbounded intervals. The simplest possible extension is to define such an integral as a limit, in other words, as an improper integral
Improper integral
In calculus, an improper integral is the limit of a definite integral as an endpoint of the interval of integration approaches either a specified real number or ∞ or −∞ or, in some cases, as both endpoints approach limits....
. We could set:
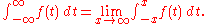
Unfortunately, this does not work well. Translation invariance, the fact that the Riemann integral of the function should not change if we move the function left or right, is lost. For example, let for all , and for all then
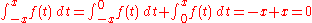
for all x. But if we shift ƒ(x) to the right by one unit to get ƒ(x−1), we get
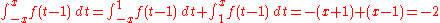
for all Since this is unacceptable, we could try the definition:
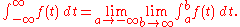
Then if we attempt to integrate the function ƒ above, we get +∞, because we take the limit first. If we reverse the order of the limits, then we get −∞.
This is also unacceptable, so we could require that the integral exists and gives the same value regardless of the order. Even this does not give us what we want, because the Riemann integral no longer commutes with uniform limits. For example, let on (0,n) and 0 everywhere else. For all n we have
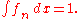
But ƒn converges uniformly to zero, so the integral of lim(ƒn) is zero. Consequently

Even though this is the correct value, it shows that the most important criterion for exchanging limits and (proper) integrals is false for improper integrals. This makes the Riemann integral unworkable in applications.
A better route is to abandon the Riemann integral for the Lebesgue integral. The definition of the Lebesgue integral is not obviously a generalization of the Riemann integral, but it is not hard to prove that every Riemann-integrable function is Lebesgue-integrable and that the values of the two integrals agree whenever they are both defined. Moreover, a function ƒ defined on a bounded interval is Riemann-integrable if and only if it is bounded and the set of points where ƒ is discontinuous has Lebesgue measure zero.
An integral which is in fact a direct generalization of the Riemann integral is the Henstock–Kurzweil integral.
Another way of generalizing the Riemann integral is to replace the factors in the definition of a Riemann sum by something else; roughly speaking, this gives the interval of integration a different notion of length. This is the approach taken by the Riemann–Stieltjes integral.