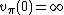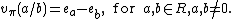Valuation (mathematics)
Encyclopedia
In algebra
(in particular in algebraic geometry
or algebraic number theory
), a valuation is a function
on a field
that provides a measure of size or multiplicity of elements of the field. They generalize to commutative algebra
the notion of size inherent in consideration of the degree of a pole or multiplicity
of a zero
in complex analysis, the degree of divisibility of a number by a prime number in number theory, and the geometrical concept of contact between two algebraic
or analytic varieties
in algebraic geometry. A field with a valuation on it is called a valued field.
The ordering and group law on Γ are extended to the set
Γ∪{∞} by the rules
Then a valuation of K is any map
which satisfies the following properties for all a, b in K:
Some authors use the term exponential valuation rather than "valuation". In this case the term "valuation" means "absolute value
".
A valuation v is called trivial (or the trivial valuation of K) if v(a) = 0 for all a in K×, otherwise it is called non-trivial.
For valuations used in geometric
applications, the first property implies that any non-empty germ
of an analytic variety near a point contains that point. The second property asserts that any valuation is a group homomorphism
, while the third property is a translation of the triangle inequality
from metric spaces to ordered groups.
It is possible to give a dual
definition of the same concept using the multiplicative notation for Γ: if, instead of ∞, an element O is given and the ordering and group law on Γ are extended by the rules
then a valuation of K is any map
satisfying the following properties for all a, b in K:
(Note that in this definition, the directions of the inequalities are reversed.)
A valuation is commonly assumed to be surjective, since many arguments used in ordinary mathematical research involving those objects use preimages of unspecified elements of the ordered group contained in its codomain
. Also, the first definition of valuation given is more frequently encountered in ordinary mathematical research, thus it is the only one used in the following considerations and examples.
such that v2(a) = φ(v1(a)) for all a in K×. This is an equivalence relation
.
Two valuations of K are equivalent if, and only if, they have the same valuation ring.
An equivalence class of valuations of a field is called a place. Ostrowski's theorem
gives a complete classification of places of the field of rational numbers Q: these are precisely the equivalence classes of valuations for the p-adic
completions
of Q.
of K. An extension of v (to L) is a valuation w of L such that the restriction of w to K is v. The set of all such extensions is studied in the ramification theory of valuations
.
Let L/K be a finite extension and let w be an extension of v to L. The index
of Γv in Γw, e(w/v) = [Γw : Γv], is called the reduced ramification index of w over v. It satisfies e(w/v) ≤ [L : K] (the degree
of the extension L/K). The relative degree of w over v is defined to be f(w/v) = [Rw/mw : Rv/mv] (the degree of the extension of residue fields). It is also less than or equal to the degree of L/K. When L/K is separable
, the ramification index of w over v is defined to be e(w/v)pi, where pi is the inseparable degree of the extension Rw/mw over Rv/mv.
on the field K. If K is complete with respect to this metric, then it is called complete valued field.
, K be its field of fractions
, and π be an irreducible element
of R. Since every principal ideal domain is a unique factorization domain
, every non-zero element a of R can be written (essentially) uniquely as
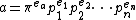
where the es are non-negative integers and the pi are irreducible elements of R that are not associates of π. In particular, the integer ea is uniquely determined by a.
The π-adic valuation of K is then given by
If π' is another irreducible element of R such that (π') = (π) (that is, they generate the same ideal in R), then the π-adic valuation and the π'-adic valuation are equal. Thus, the π-adic valuation can be called the P-adic valuation, where P = (π).
When R is the ring of integers
Z, then K is the rational number
s Q, and π is some prime number
p (or its negative). The π-adic valuation obtained is the p-adic valuation on Q.
of R at P, denoted RP, is a principal ideal domain whose field of fractions is K. The construction of the previous section applied to the prime ideal PRP of RP yields the P-adic valuation of K.
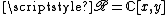be the ring of polynomials of two variables over the complex field, 
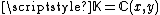be the field of rational functions over the same field, and consider the (convergent) power series
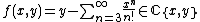
whose zero set, the analytic variety
, can be parametrized by one coordinate
as follows
It is possible to define a map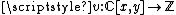
as the value of the order of the formal power series in the variable 
obtained by restriction of any polynomial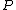 
in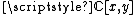 
to the points of the set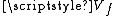 
It is also possible to extend the map
from its original ring of definition to the whole field 
as follows
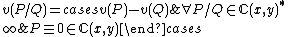
As the power series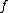
is not a polynomial
, it is easy to prove that the extended map
is a valuation: the value 
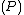is called intersection number
between the curve
s (1-dimension
al analytic varieties
)
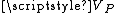and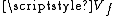 
. As an example, the computation of some intersection numbers follows
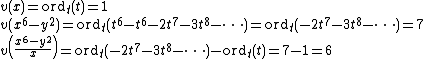
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
(in particular in algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
or algebraic number theory
Algebraic number field
In mathematics, an algebraic number field F is a finite field extension of the field of rational numbers Q...
), a valuation is a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
on a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
that provides a measure of size or multiplicity of elements of the field. They generalize to commutative algebra
Commutative algebra
Commutative algebra is the branch of abstract algebra that studies commutative rings, their ideals, and modules over such rings. Both algebraic geometry and algebraic number theory build on commutative algebra...
the notion of size inherent in consideration of the degree of a pole or multiplicity
Multiplicity (mathematics)
In mathematics, the multiplicity of a member of a multiset is the number of times it appears in the multiset. For example, the number of times a given polynomial equation has a root at a given point....
of a zero
Zero (complex analysis)
In complex analysis, a zero of a holomorphic function f is a complex number a such that f = 0.-Multiplicity of a zero:A complex number a is a simple zero of f, or a zero of multiplicity 1 of f, if f can be written asf=g\,where g is a holomorphic function g such that g is not zero.Generally, the...
in complex analysis, the degree of divisibility of a number by a prime number in number theory, and the geometrical concept of contact between two algebraic
Algebraic variety
In mathematics, an algebraic variety is the set of solutions of a system of polynomial equations. Algebraic varieties are one of the central objects of study in algebraic geometry...
or analytic varieties
Analytic variety
In mathematics, specifically geometry, an analytic variety is defined locally as the set of common zeros of finitely many analytic functions. It is analogous to the included concept of complex algebraic variety, and every complex manifold is an analytic variety. Since analytic varieties may have...
in algebraic geometry. A field with a valuation on it is called a valued field.
Definition
To define the algebraic concept of valuation, the following objects are needed:- a fieldField (mathematics)In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
K and its multiplicative subgroup K×, - an abelianAbelian groupIn abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
totally ordered group (Γ, +, ≥) (which could also be given in multiplicative notation as (Γ, ·, ≥)).
The ordering and group law on Γ are extended to the set
Set
A set is a collection of well defined and distinct objects, considered as an object in its own right. Sets are one of the most fundamental concepts in mathematics. Developed at the end of the 19th century, set theory is now a ubiquitous part of mathematics, and can be used as a foundation from...
Γ∪{∞} by the rules
- ∞ ≥ α for all α in Γ,∞ + α = α + ∞ = ∞ for all α in Γ.
Then a valuation of K is any map
Map (mathematics)
In most of mathematics and in some related technical fields, the term mapping, usually shortened to map, is either a synonym for function, or denotes a particular kind of function which is important in that branch, or denotes something conceptually similar to a function.In graph theory, a map is a...
- }
which satisfies the following properties for all a, b in K:
- v(a) = ∞ if, and only if, a = 0,v(ab) = v(a) + v(b),v(a + b) ≥ min(v(a), v(b)).
Some authors use the term exponential valuation rather than "valuation". In this case the term "valuation" means "absolute value
Absolute value (algebra)
In mathematics, an absolute value is a function which measures the "size" of elements in a field or integral domain. More precisely, if D is an integral domain, then an absolute value is any mapping | x | from D to the real numbers R satisfying:* | x | ≥ 0,*...
".
A valuation v is called trivial (or the trivial valuation of K) if v(a) = 0 for all a in K×, otherwise it is called non-trivial.
For valuations used in geometric
Analytic geometry
Analytic geometry, or analytical geometry has two different meanings in mathematics. The modern and advanced meaning refers to the geometry of analytic varieties...
applications, the first property implies that any non-empty germ
Germ (mathematics)
In mathematics, the notion of a germ of an object in/on a topological space captures the local properties of the object. In particular, the objects in question are mostly functions and subsets...
of an analytic variety near a point contains that point. The second property asserts that any valuation is a group homomorphism
Group homomorphism
In mathematics, given two groups and , a group homomorphism from to is a function h : G → H such that for all u and v in G it holds that h = h \cdot h...
, while the third property is a translation of the triangle inequality
Triangle inequality
In mathematics, the triangle inequality states that for any triangle, the sum of the lengths of any two sides must be greater than or equal to the length of the remaining side ....
from metric spaces to ordered groups.
It is possible to give a dual
Duality (mathematics)
In mathematics, a duality, generally speaking, translates concepts, theorems or mathematical structures into other concepts, theorems or structures, in a one-to-one fashion, often by means of an involution operation: if the dual of A is B, then the dual of B is A. As involutions sometimes have...
definition of the same concept using the multiplicative notation for Γ: if, instead of ∞, an element O is given and the ordering and group law on Γ are extended by the rules
- O ≤ α for all α in Γ,O · α = α · O = O for all α in Γ,
then a valuation of K is any map
- }
satisfying the following properties for all a, b in K:
- v(a) = O if, and only if, a = 0,v(ab) = v(a) · v(b),v(a + b) ≤ max(v(a), v(b)).
(Note that in this definition, the directions of the inequalities are reversed.)
A valuation is commonly assumed to be surjective, since many arguments used in ordinary mathematical research involving those objects use preimages of unspecified elements of the ordered group contained in its codomain
Codomain
In mathematics, the codomain or target set of a function is the set into which all of the output of the function is constrained to fall. It is the set in the notation...
. Also, the first definition of valuation given is more frequently encountered in ordinary mathematical research, thus it is the only one used in the following considerations and examples.
Associated objects
If } is a valuation, then there are several objects that can be defined from it:- the value group of v (or valuation group of v), denoted Γv, is v(K×), it is a subgroup of Γ,
- the valuation ring of v, denoted Rv is the set of elements a of K such that v(a) ≥ 0, it is a valuation ringValuation ringIn abstract algebra, a valuation ring is an integral domain D such that for every element x of its field of fractions F, at least one of x or x −1 belongs to D....
, - the prime ideal of v (or the maximal ideal of v), denoted mv is the set of elements a of K such that v(a) > 0, it is a maximal idealMaximal idealIn mathematics, more specifically in ring theory, a maximal ideal is an ideal which is maximal amongst all proper ideals. In other words, I is a maximal ideal of a ring R if I is an ideal of R, I ≠ R, and whenever J is another ideal containing I as a subset, then either J = I or J = R...
of Rv, - the residue field of v, denoted kv is Rv/mv, it is a field.
Equivalence of valuations
Two valuations v1 and v2 of K with valuation group Γ1 and Γ2, respectively, are said to be equivalent if they have there is an order-preserving group isomorphismGroup isomorphism
In abstract algebra, a group isomorphism is a function between two groups that sets up a one-to-one correspondence between the elements of the groups in a way that respects the given group operations. If there exists an isomorphism between two groups, then the groups are called isomorphic...
such that v2(a) = φ(v1(a)) for all a in K×. This is an equivalence relation
Equivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
.
Two valuations of K are equivalent if, and only if, they have the same valuation ring.
An equivalence class of valuations of a field is called a place. Ostrowski's theorem
Ostrowski's theorem
Ostrowski's theorem, due to Alexander Ostrowski , states that any non-trivial absolute value on the rational numbers Q is equivalent to either the usual real absolute value or a p-adic absolute value.- Definitions :...
gives a complete classification of places of the field of rational numbers Q: these are precisely the equivalence classes of valuations for the p-adic
P-adic number
In mathematics, and chiefly number theory, the p-adic number system for any prime number p extends the ordinary arithmetic of the rational numbers in a way different from the extension of the rational number system to the real and complex number systems...
completions
Complete space
In mathematical analysis, a metric space M is called complete if every Cauchy sequence of points in M has a limit that is also in M or, alternatively, if every Cauchy sequence in M converges in M....
of Q.
Extension of valuations
Let v be a valuation of K and let L be a field extensionField extension
In abstract algebra, field extensions are the main object of study in field theory. The general idea is to start with a base field and construct in some manner a larger field which contains the base field and satisfies additional properties...
of K. An extension of v (to L) is a valuation w of L such that the restriction of w to K is v. The set of all such extensions is studied in the ramification theory of valuations
Ramification theory of valuations
In mathematics, the ramification theory of valuations studies the set of extensions of a valuation v of a field K to an extension L of K...
.
Let L/K be a finite extension and let w be an extension of v to L. The index
Index of a subgroup
In mathematics, specifically group theory, the index of a subgroup H in a group G is the "relative size" of H in G: equivalently, the number of "copies" of H that fill up G. For example, if H has index 2 in G, then intuitively "half" of the elements of G lie in H...
of Γv in Γw, e(w/v) = [Γw : Γv], is called the reduced ramification index of w over v. It satisfies e(w/v) ≤ [L : K] (the degree
Degree of a field extension
In mathematics, more specifically field theory, the degree of a field extension is a rough measure of the "size" of the extension. The concept plays an important role in many parts of mathematics, including algebra and number theory — indeed in any area where fields appear prominently.-...
of the extension L/K). The relative degree of w over v is defined to be f(w/v) = [Rw/mw : Rv/mv] (the degree of the extension of residue fields). It is also less than or equal to the degree of L/K. When L/K is separable
Separable extension
In modern algebra, an algebraic field extension E\supseteq F is a separable extension if and only if for every \alpha\in E, the minimal polynomial of \alpha over F is a separable polynomial . Otherwise, the extension is called inseparable...
, the ramification index of w over v is defined to be e(w/v)pi, where pi is the inseparable degree of the extension Rw/mw over Rv/mv.
Complete valued fields
When the ordered abelian group Γ is the additive group of the integers, the associated absolute value induces a metricMetric (mathematics)
In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...
on the field K. If K is complete with respect to this metric, then it is called complete valued field.
π-adic valuation
Let R be a principal ideal domainPrincipal ideal domain
In abstract algebra, a principal ideal domain, or PID, is an integral domain in which every ideal is principal, i.e., can be generated by a single element. More generally, a principal ideal ring is a nonzero commutative ring whose ideals are principal, although some authors refer to PIDs as...
, K be its field of fractions
Field of fractions
In abstract algebra, the field of fractions or field of quotients of an integral domain is the smallest field in which it can be embedded. The elements of the field of fractions of the integral domain R have the form a/b with a and b in R and b ≠ 0...
, and π be an irreducible element
Irreducible element
In abstract algebra, a non-zero non-unit element in an integral domain is said to be irreducible if it is not a product of two non-units.Irreducible elements should not be confused with prime elements...
of R. Since every principal ideal domain is a unique factorization domain
Unique factorization domain
In mathematics, a unique factorization domain is, roughly speaking, a commutative ring in which every element, with special exceptions, can be uniquely written as a product of prime elements , analogous to the fundamental theorem of arithmetic for the integers...
, every non-zero element a of R can be written (essentially) uniquely as
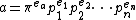
where the es are non-negative integers and the pi are irreducible elements of R that are not associates of π. In particular, the integer ea is uniquely determined by a.
The π-adic valuation of K is then given by
If π' is another irreducible element of R such that (π') = (π) (that is, they generate the same ideal in R), then the π-adic valuation and the π'-adic valuation are equal. Thus, the π-adic valuation can be called the P-adic valuation, where P = (π).
When R is the ring of integers
Ring of integers
In mathematics, the ring of integers is the set of integers making an algebraic structure Z with the operations of integer addition, negation, and multiplication...
Z, then K is the rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s Q, and π is some prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
p (or its negative). The π-adic valuation obtained is the p-adic valuation on Q.
P-adic valuation on a Dedekind domain
The previous example can be generalized to Dedekind domains. Let R be a Dedekind domain, K its field of fractions, and let P be a non-zero prime ideal of R. Then, the localizationLocalization of a ring
In abstract algebra, localization is a systematic method of adding multiplicative inverses to a ring. Given a ring R and a subset S, one wants to construct some ring R* and ring homomorphism from R to R*, such that the image of S consists of units in R*...
of R at P, denoted RP, is a principal ideal domain whose field of fractions is K. The construction of the previous section applied to the prime ideal PRP of RP yields the P-adic valuation of K.
Geometric notion of contact
Let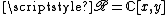 be the ring of polynomials of two variables over the complex field, 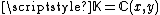be the field of rational functions over the same field, and consider the (convergent) power series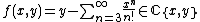whose zero set, the analytic variety
, can be parametrized by one coordinateCoordinate system
In geometry, a coordinate system is a system which uses one or more numbers, or coordinates, to uniquely determine the position of a point or other geometric element. The order of the coordinates is significant and they are sometimes identified by their position in an ordered tuple and sometimes by...
as followsIt is possible to define a map
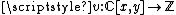as the value of the order of the formal power series in the variable obtained by restriction of any polynomial 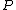in 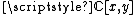to the points of the set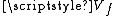 It is also possible to extend the map
from its original ring of definition to the whole field as follows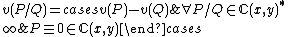As the power series
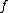is not a polynomialPolynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
, it is easy to prove that the extended map
is a valuation: the value 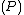is called intersection numberIntersection number
In mathematics, and especially in algebraic geometry, the intersection number generalizes the intuitive notion of counting the number of times two curves intersect to higher dimensions, multiple curves, and accounting properly for tangency...
between the curve
Curve
In mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...
s (1-dimension
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
al analytic varieties
Analytic variety
In mathematics, specifically geometry, an analytic variety is defined locally as the set of common zeros of finitely many analytic functions. It is analogous to the included concept of complex algebraic variety, and every complex manifold is an analytic variety. Since analytic varieties may have...
)
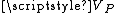and 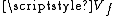. As an example, the computation of some intersection numbers follows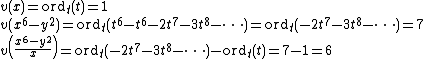See also
- Valued field
- Valuation (measure theory)Valuation (measure theory)In measure theory or at least in the approach to it through domain theory, a valuation is a map from the class of open sets of a topological space to the set positive real numbers including infinity...
- Valuation ringValuation ringIn abstract algebra, a valuation ring is an integral domain D such that for every element x of its field of fractions F, at least one of x or x −1 belongs to D....
- Discrete valuation