
Multiplicity (mathematics)
Encyclopedia
In mathematics
, the multiplicity of a member of a multiset
is the number of times it appears in the multiset. For example, the number of times a given polynomial equation has a root at a given point.
The notion of multiplicity is important to be able to count correctly without specifying exceptions (for example, double roots counted twice). Hence the expression, "counted with (sometimes implicit) multiplicity".
When mathematicians wish to ignore multiplicity they will refer to the number of distinct elements of a set.
, for example,
the multiplicity of the prime factor 2 is 2, while the multiplicity of each of the prime factors 3 and 5 is 1. Thus, 60 has 4 prime factors, but only 3 distinct prime factors.
and p(x) be a polynomial
in one variable and coefficients in F. An element a ∈ F is called a root of multiplicity k of p(x) if there is a polynomial s(x) such that s(a) ≠ 0 and p(x) = (x − a)ks(x). If k = 1, then a is called a simple root.
For instance, the polynomial p(x) = x3 + 2x2 − 7x + 4 has 1 and −4 as roots, and can be written as p(x) = (x + 4)(x − 1)2. This means that 1 is a root of multiplicity 2, and −4 is a 'simple' root (of multiplicity 1). Multiplicity can be thought of as "How many times does the solution appear in the original equation?".
The discriminant of a polynomial is zero if and only if the polynomial has a multiple root.
function. Then, if f is graphed on a Cartesian coordinate system
, its graph will cross the x-axis at real zeros of odd multiplicity and will touch but not cross the x-axis at real zeros of even multiplicity. In addition, if f(x) has a zero with a multiplicity greater than 1, the graph will be tangent to the x-axis, in other words it will have slope 0 there.
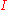 be an interval of R, let
be an interval of R, let  be a function from
be a function from 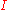 into R or C be a real (resp. complex) function, and let
into R or C be a real (resp. complex) function, and let  ∈
∈ 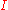 be a zero of
be a zero of  , i.e. a point such that
, i.e. a point such that 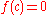 . The point
. The point  is said a zero of multiplicity
is said a zero of multiplicity 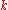 of
of  if there exist a real number
if there exist a real number  such that
such that
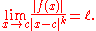
In a more general setting, let be a function from an open subset
be a function from an open subset  of a normed vector space
of a normed vector space
 into a normed vector space
into a normed vector space  , and let
, and let 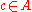 be a zero of
be a zero of  , i.e. a point such that
, i.e. a point such that 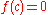 . The point
. The point  is said a zero of multiplicity
is said a zero of multiplicity 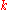 of
of  if there exist a real number
if there exist a real number 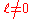 such that
such that
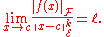
The point is said a zero of multiplicity ∞ of
is said a zero of multiplicity ∞ of  if for each
if for each 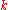 , it holds that
, it holds that
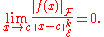
Example 1. Since

0 is a zero of multiplicity 1 for the sine function.
Example 2. Since
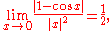
0 is a zero of multiplicity 2 for the function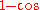 .
.
Example 3. Consider the function from R into R such that
from R into R such that 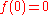 and that
and that 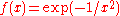 when
when 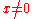 . Then, since
. Then, since

0 is a zero of multiplicity ∞ for the function .
.
ƒ, and let n be the least positive integer such that, the nth derivative of ƒ evaluated at z0 differs from zero. Then the power series of ƒ about z0 begins with the nth term, and ƒ is said to have a root of multiplicity (or “order”) n. If n = 1, the root is called a simple root (Krantz 1999, p. 70).
We can also define the multiplicity of the zeroes and poles of a meromorphic function
thus: If we have a meromorphic function ƒ = g/h, take the Taylor expansions
of g and h about a point z0, and find the first non-zero term in each (denote the term numbers m and n respectively). if m = n, then the point has non-zero value. If m > n, then the point is a zero of multiplicity m − n. If m < n, then the point has a pole of multiplicity n − m.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the multiplicity of a member of a multiset
Multiset
In mathematics, the notion of multiset is a generalization of the notion of set in which members are allowed to appear more than once...
is the number of times it appears in the multiset. For example, the number of times a given polynomial equation has a root at a given point.
The notion of multiplicity is important to be able to count correctly without specifying exceptions (for example, double roots counted twice). Hence the expression, "counted with (sometimes implicit) multiplicity".
When mathematicians wish to ignore multiplicity they will refer to the number of distinct elements of a set.
Multiplicity of a prime factor
In the prime factorizationInteger factorization
In number theory, integer factorization or prime factorization is the decomposition of a composite number into smaller non-trivial divisors, which when multiplied together equal the original integer....
, for example,
- 60 = 2 × 2 × 3 × 5
the multiplicity of the prime factor 2 is 2, while the multiplicity of each of the prime factors 3 and 5 is 1. Thus, 60 has 4 prime factors, but only 3 distinct prime factors.
Multiplicity of a root of a polynomial
Let F be a fieldField (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
and p(x) be a polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
in one variable and coefficients in F. An element a ∈ F is called a root of multiplicity k of p(x) if there is a polynomial s(x) such that s(a) ≠ 0 and p(x) = (x − a)ks(x). If k = 1, then a is called a simple root.
For instance, the polynomial p(x) = x3 + 2x2 − 7x + 4 has 1 and −4 as roots, and can be written as p(x) = (x + 4)(x − 1)2. This means that 1 is a root of multiplicity 2, and −4 is a 'simple' root (of multiplicity 1). Multiplicity can be thought of as "How many times does the solution appear in the original equation?".
The discriminant of a polynomial is zero if and only if the polynomial has a multiple root.
Behavior of a polynomial function near a root in relation to its multiplicity
Let f(x) be a polynomialPolynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
function. Then, if f is graphed on a Cartesian coordinate system
Cartesian coordinate system
A Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...
, its graph will cross the x-axis at real zeros of odd multiplicity and will touch but not cross the x-axis at real zeros of even multiplicity. In addition, if f(x) has a zero with a multiplicity greater than 1, the graph will be tangent to the x-axis, in other words it will have slope 0 there.
Multiplicity of a zero of a function
Let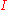 be an interval of R, let
be an interval of R, let  be a function from
be a function from 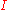 into R or C be a real (resp. complex) function, and let
into R or C be a real (resp. complex) function, and let  ∈
∈ 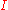 be a zero of
be a zero of  , i.e. a point such that
, i.e. a point such that 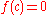 . The point
. The point  is said a zero of multiplicity
is said a zero of multiplicity 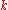 of
of  if there exist a real number
if there exist a real number  such that
such that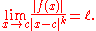
In a more general setting, let
 be a function from an open subset
be a function from an open subset  of a normed vector space
of a normed vector spaceNormed vector space
In mathematics, with 2- or 3-dimensional vectors with real-valued entries, the idea of the "length" of a vector is intuitive and can easily be extended to any real vector space Rn. The following properties of "vector length" are crucial....
 into a normed vector space
into a normed vector space  , and let
, and let 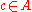 be a zero of
be a zero of  , i.e. a point such that
, i.e. a point such that 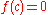 . The point
. The point  is said a zero of multiplicity
is said a zero of multiplicity 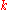 of
of  if there exist a real number
if there exist a real number 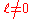 such that
such that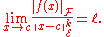
The point
 is said a zero of multiplicity ∞ of
is said a zero of multiplicity ∞ of  if for each
if for each 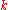 , it holds that
, it holds that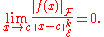
Example 1. Since

0 is a zero of multiplicity 1 for the sine function.
Example 2. Since
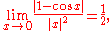
0 is a zero of multiplicity 2 for the function
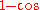 .
.Example 3. Consider the function
 from R into R such that
from R into R such that 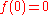 and that
and that 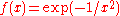 when
when 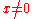 . Then, since
. Then, since
0 is a zero of multiplicity ∞ for the function
 .
.In complex analysis
Let z0 be a root of a holomorphic functionHolomorphic function
In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
ƒ, and let n be the least positive integer such that, the nth derivative of ƒ evaluated at z0 differs from zero. Then the power series of ƒ about z0 begins with the nth term, and ƒ is said to have a root of multiplicity (or “order”) n. If n = 1, the root is called a simple root (Krantz 1999, p. 70).
We can also define the multiplicity of the zeroes and poles of a meromorphic function
Meromorphic function
In complex analysis, a meromorphic function on an open subset D of the complex plane is a function that is holomorphic on all D except a set of isolated points, which are poles for the function...
thus: If we have a meromorphic function ƒ = g/h, take the Taylor expansions
Taylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
of g and h about a point z0, and find the first non-zero term in each (denote the term numbers m and n respectively). if m = n, then the point has non-zero value. If m > n, then the point is a zero of multiplicity m − n. If m < n, then the point has a pole of multiplicity n − m.
See also
- Zero (complex analysis)Zero (complex analysis)In complex analysis, a zero of a holomorphic function f is a complex number a such that f = 0.-Multiplicity of a zero:A complex number a is a simple zero of f, or a zero of multiplicity 1 of f, if f can be written asf=g\,where g is a holomorphic function g such that g is not zero.Generally, the...
- Set (mathematics)
- Fundamental theorem of algebraFundamental theorem of algebraThe fundamental theorem of algebra states that every non-constant single-variable polynomial with complex coefficients has at least one complex root...
- Fundamental theorem of arithmeticFundamental theorem of arithmeticIn number theory, the fundamental theorem of arithmetic states that any integer greater than 1 can be written as a unique product of prime numbers...
- Algebraic multiplicity and geometric multiplicity of an eigenvalue
- Frequency (statistics)Frequency (statistics)In statistics the frequency of an event i is the number ni of times the event occurred in the experiment or the study. These frequencies are often graphically represented in histograms....

