Unique factorization domain - AbsoluteAstronomy.com

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, a unique factorization domain (UFD) is, roughly speaking, a commutative ring

Commutative ring

In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....

in which every element, with special exceptions, can be uniquely written as a product of prime element

Prime element

In abstract algebra, an element p of a commutative ring R is said to be prime if it is not zero, not a unit and whenever p divides ab for some a and b in R, then p divides a or p divides b...

s (or irreducible element

Irreducible element

In abstract algebra, a non-zero non-unit element in an integral domain is said to be irreducible if it is not a product of two non-units.Irreducible elements should not be confused with prime elements...

s), analogous to the fundamental theorem of arithmetic

Fundamental theorem of arithmetic

In number theory, the fundamental theorem of arithmetic states that any integer greater than 1 can be written as a unique product of prime numbers...

for the integer

Integer

The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...

s. UFDs are sometimes called factorial rings, following the terminology of Bourbaki

Nicolas Bourbaki

Nicolas Bourbaki is the collective pseudonym under which a group of 20th-century mathematicians wrote a series of books presenting an exposition of modern advanced mathematics, beginning in 1935. With the goal of founding all of mathematics on set theory, the group strove for rigour and generality...

.

Note that unique factorization domains appear in the following chain of class inclusions:

Commutative ring
Commutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....

s ⊃ integral domains ⊃ integrally closed domain
Integrally closed domain
In commutative algebra, an integrally closed domain A is an integral domain whose integral closure in the field of fractions of A is A itself...

s ⊃ unique factorization domains ⊃ principal ideal domain
Principal ideal domain
In abstract algebra, a principal ideal domain, or PID, is an integral domain in which every ideal is principal, i.e., can be generated by a single element. More generally, a principal ideal ring is a nonzero commutative ring whose ideals are principal, although some authors refer to PIDs as...

s ⊃ Euclidean domain
Euclidean domain
In mathematics, more specifically in abstract algebra and ring theory, a Euclidean domain is a ring that can be endowed with a certain structure – namely a Euclidean function, to be described in detail below – which allows a suitable generalization of the Euclidean algorithm...

s ⊃ field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...

s

Definition

Formally, a unique factorization domain is defined to be an integral domain R in which every non-zero x of R can be written as a product (including an empty product

Empty product

In mathematics, an empty product, or nullary product, is the result of multiplying no factors. It is equal to the multiplicative identity 1, given that it exists for the multiplication operation in question, just as the empty sum—the result of adding no numbers—is zero, or the additive...

) of irreducible element

Irreducible element

s p_i of R and a unit

Unit (ring theory)

In mathematics, an invertible element or a unit in a ring R refers to any element u that has an inverse element in the multiplicative monoid of R, i.e. such element v that...

x = u p₁ p₂ ... p_n with n≥0

and this representation is unique in the following sense:
If q₁,...,q_m are irreducible elements of R and w is a unit such that

x = w q₁ q₂ ... q_m with m≥0,

then m = n and there exists a bijective map φ : {1,...,n} -> {1,...,m} such that p_i is associated to q_φ(i) for i ∈ {1, ..., n}.

The uniqueness part is usually hard to verify, which is why the following equivalent definition is useful:

A unique factorization domain is an integral domain R in which every non-zero element can be written as a product of a unit and prime element

Prime element

In abstract algebra, an element p of a commutative ring R is said to be prime if it is not zero, not a unit and whenever p divides ab for some a and b in R, then p divides a or p divides b...

s of R.

Examples

Most rings familiar from elementary mathematics are UFDs:

All principal ideal domain
Principal ideal domain
In abstract algebra, a principal ideal domain, or PID, is an integral domain in which every ideal is principal, i.e., can be generated by a single element. More generally, a principal ideal ring is a nonzero commutative ring whose ideals are principal, although some authors refer to PIDs as...

s, hence all Euclidean domain
Euclidean domain
In mathematics, more specifically in abstract algebra and ring theory, a Euclidean domain is a ring that can be endowed with a certain structure – namely a Euclidean function, to be described in detail below – which allows a suitable generalization of the Euclidean algorithm...

s, are UFDs. In particular, the integers (also see fundamental theorem of arithmetic
Fundamental theorem of arithmetic
In number theory, the fundamental theorem of arithmetic states that any integer greater than 1 can be written as a unique product of prime numbers...

), the Gaussian integer
Gaussian integer
In number theory, a Gaussian integer is a complex number whose real and imaginary part are both integers. The Gaussian integers, with ordinary addition and multiplication of complex numbers, form an integral domain, usually written as Z[i]. The Gaussian integers are a special case of the quadratic...

s and the Eisenstein integer
Eisenstein integer
In mathematics, Eisenstein integers , also known as Eulerian integers , are complex numbers of the formz = a + b\omega \,\!where a and b are integers and...

s are UFDs.
Any field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...

is trivially a UFD, since every non-zero element is a unit. Examples of fields include rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...

s, real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...

s, and complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...

s.
If R is a UFD, then so is R[X], the ring of polynomials
Polynomial ring
In mathematics, especially in the field of abstract algebra, a polynomial ring is a ring formed from the set of polynomials in one or more variables with coefficients in another ring. Polynomial rings have influenced much of mathematics, from the Hilbert basis theorem, to the construction of...

with coefficients in R. Unless R is a field, R[X] is not a principal ideal domain. By iteration, a polynomial ring in any number of variables over any UFD (and in particular over a field) is an UFD.
The Auslander–Buchsbaum theorem
Auslander–Buchsbaum theorem
In commutative algebra, the Auslander–Buchsbaum theorem states that regular local rings are unique factorization domains.The theorem was first proved by . They showed that regular local rings of dimension 3 are unique factorization domains, and had previously shown that this implies that all...

states that every regular local ring
Regular local ring
In commutative algebra, a regular local ring is a Noetherian local ring having the property that the minimal number of generators of its maximal ideal is equal to its Krull dimension. In symbols, let A be a Noetherian local ring with maximal ideal m, and suppose a1, ..., an is a minimal set of...

is a UFD.

Further examples of UFDs are:

The formal power series
Formal power series
In mathematics, formal power series are a generalization of polynomials as formal objects, where the number of terms is allowed to be infinite; this implies giving up the possibility to substitute arbitrary values for indeterminates...

ring KX₁,...,X_n over a field K (or more generally over a PID but not over a UFD).

Non-examples

The quadratic integer ring of all complex numbers of the form 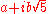, where a and b are integers. Then 6 factors as both (2)(3) and as 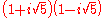. These truly are different factorizations, because the only units in this ring are 1 and −1; thus, none of 2, 3, , and 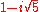are associate
Unit (ring theory)
In mathematics, an invertible element or a unit in a ring R refers to any element u that has an inverse element in the multiplicative monoid of R, i.e. such element v that...

. It is not hard to show that all four factors are irreducible as well, though this may not be obvious. See also algebraic integer
Algebraic integer
In number theory, an algebraic integer is a complex number that is a root of some monic polynomial with coefficients in . The set of all algebraic integers is closed under addition and multiplication and therefore is a subring of complex numbers denoted by A...

.

Most factor ring
Ideal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....

s of a polynomial ring are not UFDs. Here are two examples:

Let be any commutative ring. Then is not a UFD. The proof is in two parts.

First we must show

, and

are all irreducible. Grade

by degree. Assume for a contradiction that

has a factorization into two non-zero non-units. Since it is degree one, the two factors must be a degree one element

and a degree zero element

. This gives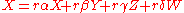

. In

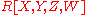, then, the degree one element

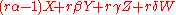must be an element of the ideal

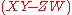, but the non-zero elements of that ideal are degree two and higher. Consequently,

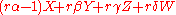must be zero in

. That implies that

, so

is a unit, which is a contradiction.

, and

are irreducible by the same argument.

Next, the element

equals the element

because of the relation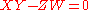

. That means that

and

are two different factorizations of the same element into irreducibles, so

is not a UFD.

The ring of holomorphic functions in a single complex variable is not a UFD, since there exist holomorphic functions with an infinity of zeros, and thus an infinity of irreducible factors, while a UFD factorization must be finite, e.g.:

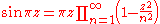A Noetherian domain
Noetherian ring
In mathematics, more specifically in the area of modern algebra known as ring theory, a Noetherian ring, named after Emmy Noether, is a ring in which every non-empty set of ideals has a maximal element...

is not necessarily a UFD. Although any non-zero non-unit
Unit (ring theory)
In mathematics, an invertible element or a unit in a ring R refers to any element u that has an inverse element in the multiplicative monoid of R, i.e. such element v that...

in a Noetherian domain is the product of irreducible elements, this product is not necessarily unique.

Properties

Some concepts defined for integers can be generalized to UFDs:

In UFDs, every irreducible element
Irreducible element
In abstract algebra, a non-zero non-unit element in an integral domain is said to be irreducible if it is not a product of two non-units.Irreducible elements should not be confused with prime elements...

is prime
Prime element
In abstract algebra, an element p of a commutative ring R is said to be prime if it is not zero, not a unit and whenever p divides ab for some a and b in R, then p divides a or p divides b...

. (In any integral domain, every prime element is irreducible, but the converse does not always hold.) Note that this has a partial converse: any Noetherian domain
Noetherian ring
In mathematics, more specifically in the area of modern algebra known as ring theory, a Noetherian ring, named after Emmy Noether, is a ring in which every non-empty set of ideals has a maximal element...

is a UFD if every irreducible element is prime.

Any two (or finitely many) elements of a UFD have a greatest common divisor
Greatest common divisor
In mathematics, the greatest common divisor , also known as the greatest common factor , or highest common factor , of two or more non-zero integers, is the largest positive integer that divides the numbers without a remainder.For example, the GCD of 8 and 12 is 4.This notion can be extended to...

and a least common multiple
Least common multiple
In arithmetic and number theory, the least common multiple of two integers a and b, usually denoted by LCM, is the smallest positive integer that is a multiple of both a and b...

. Here, a greatest common divisor of a and b is an element d which divides
Divisor
In mathematics, a divisor of an integer n, also called a factor of n, is an integer which divides n without leaving a remainder.-Explanation:...

both a and b, and such that every other common divisor of a and b divides d. All greatest common divisors of a and b are associated.

Any UFD is integrally closed
Integrally closed
In mathematics, more specifically in abstract algebra, the concept of integrally closed has two meanings, one for groups and one for rings. -Commutative rings:...

. In other words, if R is an integral domain with quotient field K, and if an element k in K is a root of a monic polynomial with coefficients in R, then k is an element of R.

Equivalent conditions for a ring to be a UFD

A Noetherian

Noetherian ring

In mathematics, more specifically in the area of modern algebra known as ring theory, a Noetherian ring, named after Emmy Noether, is a ring in which every non-empty set of ideals has a maximal element...

integral domain is a UFD if and only if

If and only if

In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....

every height 1 prime ideal

Prime ideal

In algebra , a prime ideal is a subset of a ring which shares many important properties of a prime number in the ring of integers...

is principal. Also, a Dedekind domain

Dedekind domain

In abstract algebra, a Dedekind domain or Dedekind ring, named after Richard Dedekind, is an integral domain in which every nonzero proper ideal factors into a product of prime ideals. It can be shown that such a factorization is then necessarily unique up to the order of the factors...

is a UFD if and only if its ideal class group

Ideal class group

In mathematics, the extent to which unique factorization fails in the ring of integers of an algebraic number field can be described by a certain group known as an ideal class group...

is trivial. In this case it is in fact a principal ideal domain

Principal ideal domain

In abstract algebra, a principal ideal domain, or PID, is an integral domain in which every ideal is principal, i.e., can be generated by a single element. More generally, a principal ideal ring is a nonzero commutative ring whose ideals are principal, although some authors refer to PIDs as...

.

There are also equivalent conditions for non-noetherian integral domains. Let A be an integral domain. Then the following are equivalent.

A is a UFD.
Every nonzero prime ideal
Prime ideal
In algebra , a prime ideal is a subset of a ring which shares many important properties of a prime number in the ring of integers...

of A contains a prime element
Prime element
In abstract algebra, an element p of a commutative ring R is said to be prime if it is not zero, not a unit and whenever p divides ab for some a and b in R, then p divides a or p divides b...

. (Kaplansky
Irving Kaplansky
Irving Kaplansky was a Canadian mathematician.-Biography:He was born in Toronto, Ontario, Canada, after his parents emigrated from Poland and attended the University of Toronto as an undergraduate. After receiving his Ph.D...

)
A satisfies ascending chain condition on principal ideals
Ascending chain condition on principal ideals
In abstract algebra, the ascending chain condition can be applied to the posets of principal left, principal right, or principal two-sided ideals of a ring, partially ordered by inclusion...

(ACCP), and the localization
Localization of a ring
In abstract algebra, localization is a systematic method of adding multiplicative inverses to a ring. Given a ring R and a subset S, one wants to construct some ring R* and ring homomorphism from R to R*, such that the image of S consists of units in R*...

S⁻¹A is a UFD, where S is a multiplicatively closed subset of A generated by prime elements. (Nagata criterion)
A satisfies (ACCP) and every irreducible
Irreducible element
In abstract algebra, a non-zero non-unit element in an integral domain is said to be irreducible if it is not a product of two non-units.Irreducible elements should not be confused with prime elements...

is prime
Prime element
In abstract algebra, an element p of a commutative ring R is said to be prime if it is not zero, not a unit and whenever p divides ab for some a and b in R, then p divides a or p divides b...

.
A is a GCD domain
GCD domain
In mathematics, a GCD domain is an integral domain R with the property that any two non-zero elements have a greatest common divisor . Equivalently, any two non-zero elements of R have a least common multiple ....

(i.e., any two elements have a greatest common divisor) satisfying (ACCP).
A is a Schreier domain
Schreier domain
In algebra, a Schreier domain is an integrally closed integral domain where every nonzero element is primal; i.e., whenever x divides yz, x can be written as x = x1 x2 so that x1 divides y and x2 divides z. An integral domain is said to be pre-Schreier if every nonzero element is primal. A GCD...

, and every nonzero nonunit can be expressed as a finite product of irreducible elements (that is, A is atomic
Atomic domain
In mathematics, more specifically ring theory, an atomic domain or factorization domain is an integral domain, every non-zero non-unit of which can be written as a product of irreducible elements...

.)
A has a divisor theory in which every divisor is principal.

In practice, (2) and (3) are the most useful conditions to check. For example, it follows immediately from (2) that a PID is a UFD, since, in a PID, every prime ideal is generated by a prime element.

The source of this article is wikipedia, the free encyclopedia. The text of this article is licensed under the GFDL.