Unit circle
Encyclopedia
In mathematics
, a unit circle is a circle
with a radius
of one. Frequently, especially in trigonometry
, "the" unit circle is the circle of radius one centered at the origin (0, 0) in the Cartesian coordinate system
in the Euclidean plane. The unit circle is often denoted S1; the generalization to higher dimensions is the unit sphere
.
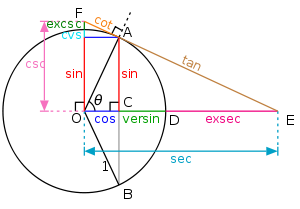
If (x, y) is a point on the unit circle in the first quadrant, then x and y are the lengths of the legs of a right triangle
whose hypotenuse has length 1. Thus, by the Pythagorean theorem
, x and y satisfy the equation
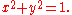
Since x2 = (−x)2 for all x, and since the reflection of any point on the unit circle about the x- or y-axis is also on the unit circle, the above equation holds for all points (x, y) on the unit circle, not just those in the first quadrant.
One may also use other notions of "distance" to define other "unit circles", such as the Riemannian circle
; see the article on mathematical norms
for additional examples.
The trigonometric function
s cosine and sine may be defined on the unit circle as follows. If (x, y) is a point of the unit circle, and if the ray from the origin (0, 0) to (x, y) makes an angle
t from the positive x-axis, (where counterclockwise turning is positive), then
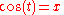
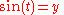
The equation x2 + y2 = 1 gives the relation
The unit circle also demonstrates that sine
and cosine are periodic function
s, with the identities
for any integer
k.
Triangles constructed on the unit circle can also be used to illustrate the periodicity of the trigonometric functions. First, construct a radius OA from the origin to a point P(x1,y1) on the unit circle such that an angle t with 0 < t < π/2 is formed with the positive arm of the x-axis. Now consider a point Q(x1,0) and line segments PQ
OQ. The result is a right triangle ΔOPQ with ∠QOP = t. Because PQ has length y1, OQ length x1, and OA length 1, sin(t) = y1 and cos(t) = x1. Having established these equivalences, take another radius OR from the origin to a point R(−x1,y1) on the circle such that the same angle t is formed with the negative arm of the x-axis. Now consider a point S(−x1,0) and line segments RS 
OS. The result is a right triangle ΔORS with ∠SOR = t. It can hence be seen that, because ∠ROQ = π−t, R is at (cos(π−t),sin(π−t)) in the same way that P is at (cos(t),sin(t)). The conclusion is that, since (−x1,y1) is the same as (cos(π−t),sin(π−t)) and (x1,y1) is the same as (cos(t),sin(t)), it is true that sin(t) = sin(π−t) and −cos(t) = cos(π−t). It may be inferred in a similar manner that tan(π−t) = −tan(t), since tan(t) = y1/x1 and tan(π−t) = y1/(−x1). A simple demonstration of the above can be seen in the equality sin(π/4) = sin(3π/4) = 1/sqrt(2).
When working with right triangles, sine, cosine, and other trigonometric functions only make sense for angle measures more than zero and less than π/2. However, when defined with the unit circle, these functions produce meaningful values for any real
-valued angle measure – even those greater than 2π. In fact, all six standard trigonometric functions – sine, cosine, tangent, cotangent, secant, and cosecant, as well as archaic functions like versine
and exsecant – can be defined geometrically in terms of a unit circle, as shown at right.
Using the unit circle, the values of any trigonometric function for many angles other than those labeled can be calculated without the use of a calculator by using the Sum and Difference Formulas.
s can be identified with points in the Euclidean plane, namely the number a + bi is identified with the point (a, b). Under this identification, the unit circle is a group
under multiplication, called the circle group. This group has important applications in mathematics and science.
Julia set of discrete nonlinear dynamical system
with evolution function:
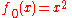
is a unit circle. It is a simplest case so it is widely used in study of dynamical systems.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a unit circle is a circle
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
with a radius
Radius
In classical geometry, a radius of a circle or sphere is any line segment from its center to its perimeter. By extension, the radius of a circle or sphere is the length of any such segment, which is half the diameter. If the object does not have an obvious center, the term may refer to its...
of one. Frequently, especially in trigonometry
Trigonometry
Trigonometry is a branch of mathematics that studies triangles and the relationships between their sides and the angles between these sides. Trigonometry defines the trigonometric functions, which describe those relationships and have applicability to cyclical phenomena, such as waves...
, "the" unit circle is the circle of radius one centered at the origin (0, 0) in the Cartesian coordinate system
Cartesian coordinate system
A Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...
in the Euclidean plane. The unit circle is often denoted S1; the generalization to higher dimensions is the unit sphere
Unit sphere
In mathematics, a unit sphere is the set of points of distance 1 from a fixed central point, where a generalized concept of distance may be used; a closed unit ball is the set of points of distance less than or equal to 1 from a fixed central point...
.
If (x, y) is a point on the unit circle in the first quadrant, then x and y are the lengths of the legs of a right triangle
Right triangle
A right triangle or right-angled triangle is a triangle in which one angle is a right angle . The relation between the sides and angles of a right triangle is the basis for trigonometry.-Terminology:The side opposite the right angle is called the hypotenuse...
whose hypotenuse has length 1. Thus, by the Pythagorean theorem
Pythagorean theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a relation in Euclidean geometry among the three sides of a right triangle...
, x and y satisfy the equation
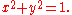
Since x2 = (−x)2 for all x, and since the reflection of any point on the unit circle about the x- or y-axis is also on the unit circle, the above equation holds for all points (x, y) on the unit circle, not just those in the first quadrant.
One may also use other notions of "distance" to define other "unit circles", such as the Riemannian circle
Riemannian circle
In metric space theory and Riemannian geometry, the Riemannian circle is a great circle equipped with its great-circle distance...
; see the article on mathematical norms
Norm (mathematics)
In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
for additional examples.
Forms of unit circle points
- exponential :
- trigonometric :
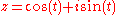
Trigonometric functions on the unit circle
Trigonometric function
In mathematics, the trigonometric functions are functions of an angle. They are used to relate the angles of a triangle to the lengths of the sides of a triangle...
s cosine and sine may be defined on the unit circle as follows. If (x, y) is a point of the unit circle, and if the ray from the origin (0, 0) to (x, y) makes an angle
Angle
In geometry, an angle is the figure formed by two rays sharing a common endpoint, called the vertex of the angle.Angles are usually presumed to be in a Euclidean plane with the circle taken for standard with regard to direction. In fact, an angle is frequently viewed as a measure of an circular arc...
t from the positive x-axis, (where counterclockwise turning is positive), then
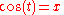
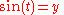
The equation x2 + y2 = 1 gives the relation
The unit circle also demonstrates that sine
Sine
In mathematics, the sine function is a function of an angle. In a right triangle, sine gives the ratio of the length of the side opposite to an angle to the length of the hypotenuse.Sine is usually listed first amongst the trigonometric functions....
and cosine are periodic function
Periodic function
In mathematics, a periodic function is a function that repeats its values in regular intervals or periods. The most important examples are the trigonometric functions, which repeat over intervals of length 2π radians. Periodic functions are used throughout science to describe oscillations,...
s, with the identities
for any integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
k.
Triangles constructed on the unit circle can also be used to illustrate the periodicity of the trigonometric functions. First, construct a radius OA from the origin to a point P(x1,y1) on the unit circle such that an angle t with 0 < t < π/2 is formed with the positive arm of the x-axis. Now consider a point Q(x1,0) and line segments PQ
OQ. The result is a right triangle ΔOPQ with ∠QOP = t. Because PQ has length y1, OQ length x1, and OA length 1, sin(t) = y1 and cos(t) = x1. Having established these equivalences, take another radius OR from the origin to a point R(−x1,y1) on the circle such that the same angle t is formed with the negative arm of the x-axis. Now consider a point S(−x1,0) and line segments RS OS. The result is a right triangle ΔORS with ∠SOR = t. It can hence be seen that, because ∠ROQ = π−t, R is at (cos(π−t),sin(π−t)) in the same way that P is at (cos(t),sin(t)). The conclusion is that, since (−x1,y1) is the same as (cos(π−t),sin(π−t)) and (x1,y1) is the same as (cos(t),sin(t)), it is true that sin(t) = sin(π−t) and −cos(t) = cos(π−t). It may be inferred in a similar manner that tan(π−t) = −tan(t), since tan(t) = y1/x1 and tan(π−t) = y1/(−x1). A simple demonstration of the above can be seen in the equality sin(π/4) = sin(3π/4) = 1/sqrt(2).When working with right triangles, sine, cosine, and other trigonometric functions only make sense for angle measures more than zero and less than π/2. However, when defined with the unit circle, these functions produce meaningful values for any real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
-valued angle measure – even those greater than 2π. In fact, all six standard trigonometric functions – sine, cosine, tangent, cotangent, secant, and cosecant, as well as archaic functions like versine
Versine
The versine or versed sine, versin, is a trigonometric function equal to and 2sin2. It appeared in some of the earliest trigonometric tables and was once widespread, but it is now little-used...
and exsecant – can be defined geometrically in terms of a unit circle, as shown at right.
Using the unit circle, the values of any trigonometric function for many angles other than those labeled can be calculated without the use of a calculator by using the Sum and Difference Formulas.
Circle group
Complex numberComplex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s can be identified with points in the Euclidean plane, namely the number a + bi is identified with the point (a, b). Under this identification, the unit circle is a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
under multiplication, called the circle group. This group has important applications in mathematics and science.
Complex dynamics
Dynamical system (definition)
The dynamical system concept is a mathematical formalization for any fixed "rule" which describes the time dependence of a point's position in its ambient space...
with evolution function:
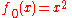
is a unit circle. It is a simplest case so it is widely used in study of dynamical systems.
See also
- Angle measureAngleIn geometry, an angle is the figure formed by two rays sharing a common endpoint, called the vertex of the angle.Angles are usually presumed to be in a Euclidean plane with the circle taken for standard with regard to direction. In fact, an angle is frequently viewed as a measure of an circular arc...
- Circle group
- Pythagorean trigonometric identityPythagorean trigonometric identityThe Pythagorean trigonometric identity is a trigonometric identity expressing the Pythagorean theorem in terms of trigonometric functions. Along with the sum-of-angles formulae, it is one the basic relations between the sine and cosine functions, from which all others may be derived.-Statement of...
- Riemannian circleRiemannian circleIn metric space theory and Riemannian geometry, the Riemannian circle is a great circle equipped with its great-circle distance...
- Unit disc
- Unit hyperbolaUnit hyperbolaIn geometry, the unit hyperbola is the set of points in the Cartesian plane that satisfies x^2 - y^2 = 1 . In the study of indefinite orthogonal groups, the unit hyperbola forms the basis for an alternative radial lengthWhereas the unit circle surrounds its center, the unit hyperbola requires the...
- Unit squareUnit squareIn mathematics, a unit square is a square whose sides have length 1. Often, "the" unit square refers specifically to the square in the Cartesian plane with corners at , , , and .-In the real plane:...
- Z-transformZ-transformIn mathematics and signal processing, the Z-transform converts a discrete time-domain signal, which is a sequence of real or complex numbers, into a complex frequency-domain representation....
External links
- Flash animation for learning the unit circle
- GonioLab: Visualization of the unit circle, trigonometric and hyperbolic functions