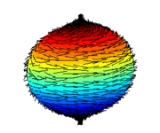
Hairy ball theorem
Encyclopedia


Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
states that there is no nonvanishing continuous
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
tangent vector field
Vector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
on an even-dimensional n-sphere. An ordinary sphere is a 2-sphere, so that this theorem will hold for an ordinary sphere. For the 2-sphere example, if f is a continuous function that assigns a vector in R3 to every point p on a sphere such that f(p) is always tangent
Tangent
In geometry, the tangent line to a plane curve at a given point is the straight line that "just touches" the curve at that point. More precisely, a straight line is said to be a tangent of a curve at a point on the curve if the line passes through the point on the curve and has slope where f...
to the sphere at p, then there is at least one p such that f(p) = 0
Null vector
Null vector can refer to:* Null vector * A causal structure in Minkowski space...
. The theorem was first stated by Henri Poincaré
Henri Poincaré
Jules Henri Poincaré was a French mathematician, theoretical physicist, engineer, and a philosopher of science...
in the late 19th century.
This is famously stated as "you can't comb a hairy ball flat without creating a cowlick
Cowlick
A cowlick is a section of hair that stands straight up or lies at an angle at odds with the style in which the rest of an individual's hair is worn. Cowlicks appear when the growth direction of the hair forms a spiral pattern. The term "cowlick" originates from the domestic bovine's habit of...
", or sometimes, "you can't comb the hair on a coconut". It was first proved in 1912 by Brouwer
Luitzen Egbertus Jan Brouwer
Luitzen Egbertus Jan Brouwer FRS , usually cited as L. E. J. Brouwer but known to his friends as Bertus, was a Dutch mathematician and philosopher, a graduate of the University of Amsterdam, who worked in topology, set theory, measure theory and complex analysis.-Biography:Early in his career,...
.
Counting zeros
From a more advanced point of view, it can be shown that the sum at the zeros of such a vector field of a certain "index" must be 2, the Euler characteristicEuler characteristic
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...
of the 2-sphere; and that therefore there must be at least some zero. This is a consequence of the Poincaré–Hopf theorem
Poincaré–Hopf theorem
In mathematics, the Poincaré–Hopf theorem is an important theorem that is still used today in differential topology...
. In the case of the torus
Torus
In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
, the Euler characteristic is 0; and it is possible to "comb a hairy doughnut flat". In this regard, it follows that for any compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
regular
Irregularity of a surface
In mathematics, the irregularity of a complex surface X is the Hodge number h0,1= dim H1, usually denoted by q . The irregularity of an algebraic surface is sometimes defined to be this Hodge number, and sometimes defined to be the dimension of the Picard variety , which is the same in...
2-dimensional manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
with non-zero Euler characteristic, any continuous tangent vector field has at least one zero.
Cyclone consequences
A curious meteorological application of this theorem involves considering the wind as a vector defined at every point continuously over the surface of a planet with an atmosphere. As an idealisation, take wind to be a two-dimensional vector: suppose that relative to the planetary diameter of the Earth, its vertical (i.e., non-tangential) motion is negligible.One scenario, in which there is absolutely no wind (air movement), corresponds to a field of zero-vectors. This scenario is uninteresting from the point of view of this theorem, and physically unrealistic (there will always be wind). In the case where there is at least some wind, the Hairy Ball Theorem dictates that at all times there must be at least one point on a planet with no wind at all and therefore a tuft. This corresponds to the above statement that there will always be p such that f(p) = 0.
In a physical sense, this zero-wind point will be the eye of a cyclone or anticyclone. (Like the swirled hairs on the tennis ball, the wind will spiral around this zero-wind point - under our assumptions it cannot flow into or out of the point.) In brief, then, the Hairy Ball Theorem dictates that, given at least some wind on Earth, there must at all times be a cyclone
Cyclone
In meteorology, a cyclone is an area of closed, circular fluid motion rotating in the same direction as the Earth. This is usually characterized by inward spiraling winds that rotate anticlockwise in the Northern Hemisphere and clockwise in the Southern Hemisphere of the Earth. Most large-scale...
somewhere. Note that the eye can be arbitrarily large or small and the magnitude of the wind surrounding it is irrelevant.
This is not strictly true as the air above the earth has multiple layers, but for each layer there must be a point with zero horizontal windspeed.
Application to computer graphics
A common problem in computer graphics is to generate a non-zero vector in R3 that is orthogonal to a given non-zero one. There is no single continuous function that can do this for all non-zero vector inputs. This is a corollary of the hairy ball theorem. To see this, consider the given vector as the radius of a sphere and note that finding a non-zero vector orthogonal to the given one is equivalent to finding a non-zero vector that is tangent to the surface of that sphere. However, the hairy ball theorem says there exists no continuous function that can do this for every point on the sphere (i.e. every given vector).Lefschetz connection
There is a closely related argument from algebraic topologyAlgebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
, using the Lefschetz fixed point theorem. Since the Betti number
Betti number
In algebraic topology, a mathematical discipline, the Betti numbers can be used to distinguish topological spaces. Intuitively, the first Betti number of a space counts the maximum number of cuts that can be made without dividing the space into two pieces....
s of a 2-sphere are 1, 0, 1, 0, 0, ... the Lefschetz number (total trace on homology
Homology (mathematics)
In mathematics , homology is a certain general procedure to associate a sequence of abelian groups or modules with a given mathematical object such as a topological space or a group...
) of the identity mapping is 2. By integrating a vector field
Vector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
we get (at least a small part of) a one-parameter group
One-parameter group
In mathematics, a one-parameter group or one-parameter subgroup usually means a continuous group homomorphismfrom the real line R to some other topological group G...
of diffeomorphism
Diffeomorphism
In mathematics, a diffeomorphism is an isomorphism in the category of smooth manifolds. It is an invertible function that maps one differentiable manifold to another, such that both the function and its inverse are smooth.- Definition :...
s on the sphere; and all of the mappings in it are homotopic to the identity. Therefore they all have Lefschetz number 2, also. Hence they have fixed points (since the Lefschetz number is nonzero). Some more work would be needed to show that this implies there must actually be a zero of the vector field. It does suggest the correct statement of the more general Poincaré-Hopf index theorem.
Corollary
A consequence of the hairy ball theorem is that any continuous functionFunction (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
that maps a sphere into itself
Endomorphism
In mathematics, an endomorphism is a morphism from a mathematical object to itself. For example, an endomorphism of a vector space V is a linear map ƒ: V → V, and an endomorphism of a group G is a group homomorphism ƒ: G → G. In general, we can talk about...
has either a fixed point
Fixed point (mathematics)
In mathematics, a fixed point of a function is a point that is mapped to itself by the function. A set of fixed points is sometimes called a fixed set...
or a point that maps onto its own antipodal point
Antipodal point
In mathematics, the antipodal point of a point on the surface of a sphere is the point which is diametrically opposite to it — so situated that a line drawn from the one to the other passes through the centre of the sphere and forms a true diameter....
. This can be seen by transforming the function into a tangential vector field as follows.
Let s be the function mapping the sphere to itself, and let v be the tangential vector function to be constructed. For each point p, construct the stereographic projection
Stereographic projection
The stereographic projection, in geometry, is a particular mapping that projects a sphere onto a plane. The projection is defined on the entire sphere, except at one point — the projection point. Where it is defined, the mapping is smooth and bijective. It is conformal, meaning that it...
of s(p) with p as the point of tangency. Then v(p) is the displacement vector of this projected point relative to p. According to the hairy ball theorem, there is a p such that v(p) = 0, so that s(p) = p.
This argument breaks down only if there exists a point p for which s(p) is the antipodal point of p, since such a point is the only one that cannot be stereographically projected onto the tangent plane of p.
Higher dimensions
The connection with the Euler characteristicEuler characteristic
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...
χ suggests the correct generalisation: the 2n-sphere
Sphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
has no non-vanishing vector field for n ≥ 1. The difference in even and odd dimension is that the Betti number
Betti number
In algebraic topology, a mathematical discipline, the Betti numbers can be used to distinguish topological spaces. Intuitively, the first Betti number of a space counts the maximum number of cuts that can be made without dividing the space into two pieces....
s of the m-sphere are 0 except in dimensions 0 and m. Therefore their alternating sum χ is 2 for m even, and 0 for m odd.

