
Unit tangent bundle
Encyclopedia
In Riemannian geometry
, a branch of mathematics
, the unit tangent bundle of a Riemannian manifold
(M, g), denoted by UT(M) or simply UTM, is the unit sphere bundle for the tangent bundle
T(M). It is a fiber bundle
over M whose fiber at each point is the unit sphere
in the tangent bundle:
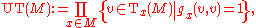
where Tx(M) denotes the tangent space
to M at x. Thus, elements of UT(M) are pairs (x, v), where x is some point of the manifold and v is some tangent direction (of unit length) to the manifold at x. The unit tangent bundle is equipped with a natural projection
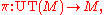
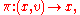
which takes each point of the bundle to its base point. The fiber π−1(x) over each point x ∈ M is an (n−1)-sphere
Sn−1, where n is the dimension of M. The unit tangent bundle is therefore a sphere bundle over M with fiber Sn−1.
The definition of unit sphere bundle can easily accommodate Finsler manifold
s as well. Specifically, if M is a manifold equipped with a Finsler metric F : TM → R, then the unit sphere bundle is the subbundle of the tangent bundle whose fiber at x is the indicatrix of F:
If M is an infinite-dimensional manifold (for example, a Banach
, Fréchet
or Hilbert manifold
), then UT(M) can still be thought of as the unit sphere bundle for the tangent bundle T(M), but the fiber π−1(x) over x is then the infinite-dimensional unit sphere in the tangent space.
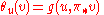
where π* is the pushforward along π of the vector v ∈ TuUTM.
Geometrically, this contact structure can be regarded as the distribution of (2n−2)-planes which, at the unit vector u, is the pullback of the orthogonal complement of u in the tangent space of M. This is a contact structure, for the fiber of UTM is obviously an integral manifold (the vertical bundle is everywhere in the kernel of θ), and the remaining tangent directions are filled out by moving up the fiber of UTM. Thus the maximal integral manifold of θ is (an open set of) M itself.
On a Finsler manifold, the contact form is defined by the analogous formula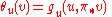
where gu is the fundamental tensor (the hessian
of the Finsler metric). Geometrically, the associated distribution of hyperplanes at the point u ∈ UTxM is the inverse image under π* of the tangent hyperplane to the unit sphere in TxM at u.
The volume form
θ∧dθn−1 defines a measure
on M, known as the kinematic measure, or Liouville measure, that is invariant under the geodesic flow of M. As a Radon measure
, the kinematic measure μ is defined on compactly supported continuous functions ƒ on UTM by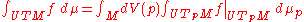
where dV is the volume element
on M, and μp is the standard rotationally-invariant Borel measure on the Euclidean sphere UTpM.
The Levi-Civita connection
of M gives rise to a splitting of the tangent bundle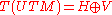
into a vertical space V = kerπ* and horizontal space H on which π* is a linear isomorphism at each point of UTM. This splitting induces a metric on UTM by declaring that this splitting be an orthogonal direct sum, and defining the metric on H by the pullback: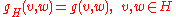
and defining the metric on V as the induced metric from the embedding of the fiber UTxM into the Euclidean space
TxM. Equipped with this metric and contact form, UTM becomes a Sasakian manifold
.
Riemannian geometry
Riemannian geometry is the branch of differential geometry that studies Riemannian manifolds, smooth manifolds with a Riemannian metric, i.e. with an inner product on the tangent space at each point which varies smoothly from point to point. This gives, in particular, local notions of angle, length...
, a branch of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the unit tangent bundle of a Riemannian manifold
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
(M, g), denoted by UT(M) or simply UTM, is the unit sphere bundle for the tangent bundle
Tangent bundle
In differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...
T(M). It is a fiber bundle
Fiber bundle
In mathematics, and particularly topology, a fiber bundle is intuitively a space which locally "looks" like a certain product space, but globally may have a different topological structure...
over M whose fiber at each point is the unit sphere
Unit sphere
In mathematics, a unit sphere is the set of points of distance 1 from a fixed central point, where a generalized concept of distance may be used; a closed unit ball is the set of points of distance less than or equal to 1 from a fixed central point...
in the tangent bundle:
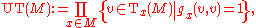
where Tx(M) denotes the tangent space
Tangent space
In mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....
to M at x. Thus, elements of UT(M) are pairs (x, v), where x is some point of the manifold and v is some tangent direction (of unit length) to the manifold at x. The unit tangent bundle is equipped with a natural projection
Projection (mathematics)
Generally speaking, in mathematics, a projection is a mapping of a set which is idempotent, which means that a projection is equal to its composition with itself. A projection may also refer to a mapping which has a left inverse. Bot notions are strongly related, as follows...
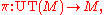
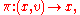
which takes each point of the bundle to its base point. The fiber π−1(x) over each point x ∈ M is an (n−1)-sphere
Hypersphere
In mathematics, an n-sphere is a generalization of the surface of an ordinary sphere to arbitrary dimension. For any natural number n, an n-sphere of radius r is defined as the set of points in -dimensional Euclidean space which are at distance r from a central point, where the radius r may be any...
Sn−1, where n is the dimension of M. The unit tangent bundle is therefore a sphere bundle over M with fiber Sn−1.
The definition of unit sphere bundle can easily accommodate Finsler manifold
Finsler manifold
In mathematics, particularly differential geometry, a Finsler manifold is a differentiable manifold together with the structure of an intrinsic quasimetric space in which the length of any rectifiable curve is given by the length functional...
s as well. Specifically, if M is a manifold equipped with a Finsler metric F : TM → R, then the unit sphere bundle is the subbundle of the tangent bundle whose fiber at x is the indicatrix of F:

If M is an infinite-dimensional manifold (for example, a Banach
Banach manifold
In mathematics, a Banach manifold is a manifold modeled on Banach spaces. Thus it is a topological space in which each point has a neighbourhood homeomorphic to an open set in a Banach space...
, Fréchet
Fréchet manifold
In mathematics, in particular in nonlinear analysis, a Fréchet manifold is a topological space modeled on a Fréchet space in much the same way as a manifold is modeled on a Euclidean space....
or Hilbert manifold
Hilbert manifold
In mathematics, a Hilbert manifold is a manifold modeled on Hilbert spaces. Thus it is a separable Hausdorff space in which each point has a neighbourhood homeomorphic to an infinite dimensional Hilbert space. The concept of a Hilbert manifold provides a possibility of extending the theory of...
), then UT(M) can still be thought of as the unit sphere bundle for the tangent bundle T(M), but the fiber π−1(x) over x is then the infinite-dimensional unit sphere in the tangent space.
Structures
The unit tangent bundle carries a variety of differential geometric structures. The metric on M induces a contact structure on UTM. This is given in terms of a tautological one-form θ, defined at a point u of UTM (a unit tangent vector of M) by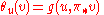
where π* is the pushforward along π of the vector v ∈ TuUTM.
Geometrically, this contact structure can be regarded as the distribution of (2n−2)-planes which, at the unit vector u, is the pullback of the orthogonal complement of u in the tangent space of M. This is a contact structure, for the fiber of UTM is obviously an integral manifold (the vertical bundle is everywhere in the kernel of θ), and the remaining tangent directions are filled out by moving up the fiber of UTM. Thus the maximal integral manifold of θ is (an open set of) M itself.
On a Finsler manifold, the contact form is defined by the analogous formula
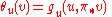
where gu is the fundamental tensor (the hessian
Hessian matrix
In mathematics, the Hessian matrix is the square matrix of second-order partial derivatives of a function; that is, it describes the local curvature of a function of many variables. The Hessian matrix was developed in the 19th century by the German mathematician Ludwig Otto Hesse and later named...
of the Finsler metric). Geometrically, the associated distribution of hyperplanes at the point u ∈ UTxM is the inverse image under π* of the tangent hyperplane to the unit sphere in TxM at u.
The volume form
Volume form
In mathematics, a volume form on a differentiable manifold is a nowhere-vanishing differential form of top degree. Thus on a manifold M of dimension n, a volume form is an n-form, a section of the line bundle Ωn = Λn, that is nowhere equal to zero. A manifold has a volume...
θ∧dθn−1 defines a measure
Measure (mathematics)
In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
on M, known as the kinematic measure, or Liouville measure, that is invariant under the geodesic flow of M. As a Radon measure
Radon measure
In mathematics , a Radon measure, named after Johann Radon, is a measure on the σ-algebra of Borel sets of a Hausdorff topological space X that is locally finite and inner regular.-Motivation:...
, the kinematic measure μ is defined on compactly supported continuous functions ƒ on UTM by
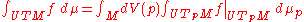
where dV is the volume element
Volume element
In mathematics, a volume element provides a means for integrating a function with respect to volume in various coordinate systems such as spherical coordinates and cylindrical coordinates...
on M, and μp is the standard rotationally-invariant Borel measure on the Euclidean sphere UTpM.
The Levi-Civita connection
Levi-Civita connection
In Riemannian geometry, the Levi-Civita connection is a specific connection on the tangent bundle of a manifold. More specifically, it is the torsion-free metric connection, i.e., the torsion-free connection on the tangent bundle preserving a given Riemannian metric.The fundamental theorem of...
of M gives rise to a splitting of the tangent bundle
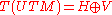
into a vertical space V = kerπ* and horizontal space H on which π* is a linear isomorphism at each point of UTM. This splitting induces a metric on UTM by declaring that this splitting be an orthogonal direct sum, and defining the metric on H by the pullback:
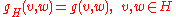
and defining the metric on V as the induced metric from the embedding of the fiber UTxM into the Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
TxM. Equipped with this metric and contact form, UTM becomes a Sasakian manifold
Sasakian manifold
In differential geometry, a Sasakian manifold is a contact manifold equipped with a special kind of Riemannian metric g, called a Sasakian metric.-Definition:...
.

