
Functional derivative
Encyclopedia
In mathematics
and theoretical physics
, the functional derivative is a generalization of the gradient
. While the latter differentiates with respect to a vector with discrete components, the former differentiates with respect to a continuous function. Both of these can be viewed as extensions of the simple one-dimensional derivative
in usual calculus
. The mathematically formal treatment is the subject of functional analysis
.
M representing (continuous/smooth
/with certain boundary conditions/etc.) functions φ and a functional
F defined as
the functional derivative of F, denoted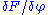 , is a distribution
, is a distribution
such that for all test functions f

Using the first variation
of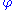 ,
,  , in place of
, in place of 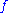 yields the first variation of
yields the first variation of 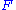 ,
, 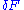 ; this is similar to how the differential
; this is similar to how the differential
is obtained from the gradient. Using a function with unit norm yields the directional derivative
with unit norm yields the directional derivative
along that function.
In physics, it's common to use the Dirac delta function
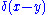 in place of a generic test function
in place of a generic test function 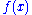 , for yielding the functional derivative at the point
, for yielding the functional derivative at the point 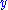 (this is a point of the whole functional derivative as a partial derivative
(this is a point of the whole functional derivative as a partial derivative
is a component of the gradient):
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
and theoretical physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, the functional derivative is a generalization of the gradient
Gradient
In vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
. While the latter differentiates with respect to a vector with discrete components, the former differentiates with respect to a continuous function. Both of these can be viewed as extensions of the simple one-dimensional derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
in usual calculus
Calculus
Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
. The mathematically formal treatment is the subject of functional analysis
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
.
Definition
Given a manifoldManifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
M representing (continuous/smooth
Smooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
/with certain boundary conditions/etc.) functions φ and a functional
Functional (mathematics)
In mathematics, and particularly in functional analysis, a functional is a map from a vector space into its underlying scalar field. In other words, it is a function that takes a vector as its input argument, and returns a scalar...
F defined as
-
 ,
,
the functional derivative of F, denoted
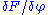 , is a distribution
, is a distributionDistribution (mathematics)
In mathematical analysis, distributions are objects that generalize functions. Distributions make it possible to differentiate functions whose derivatives do not exist in the classical sense. In particular, any locally integrable function has a distributional derivative...
such that for all test functions f

Using the first variation
First variation
In applied mathematics and the calculus of variations, the first variation of a functional J is defined as the linear functional \delta J mapping the function h to...
of
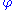 ,
,  , in place of
, in place of 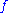 yields the first variation of
yields the first variation of 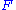 ,
, 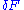 ; this is similar to how the differential
; this is similar to how the differentialDifferential
-Mathematics:* Differential comprises multiple related meanings of the word, both in calculus and differential geometry, such as an infinitesimal change in the value of a function* Differential algebra* Differential calculus...
is obtained from the gradient. Using a function
 with unit norm yields the directional derivative
with unit norm yields the directional derivativeDirectional derivative
In mathematics, the directional derivative of a multivariate differentiable function along a given vector V at a given point P intuitively represents the instantaneous rate of change of the function, moving through P in the direction of V...
along that function.
In physics, it's common to use the Dirac delta function
Dirac delta function
The Dirac delta function, or δ function, is a generalized function depending on a real parameter such that it is zero for all values of the parameter except when the parameter is zero, and its integral over the parameter from −∞ to ∞ is equal to one. It was introduced by theoretical...
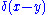 in place of a generic test function
in place of a generic test function 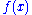 , for yielding the functional derivative at the point
, for yielding the functional derivative at the point 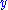 (this is a point of the whole functional derivative as a partial derivative
(this is a point of the whole functional derivative as a partial derivativePartial derivative
In mathematics, a partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant...
is a component of the gradient):
-

This works in cases when formally can be expanded as a series (or at least up to first order) in
formally can be expanded as a series (or at least up to first order) in  . The formula is however not mathematically rigorous, since
. The formula is however not mathematically rigorous, since 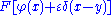 is usually not even defined.
is usually not even defined.
Formal description
The definition of a functional derivative may be made more mathematically precise and formal by defining the space of functionsTopological vector spaceIn mathematics, a topological vector space is one of the basic structures investigated in functional analysis...
more carefully. For example, when the space of functions is a Banach spaceBanach spaceIn mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
, the functional derivative becomes known as the Fréchet derivativeFréchet derivativeIn mathematics, the Fréchet derivative is a derivative defined on Banach spaces. Named after Maurice Fréchet, it is commonly used to formalize the concept of the functional derivative used widely in the calculus of variations. Intuitively, it generalizes the idea of linear approximation from...
, while one uses the Gâteaux derivativeGâteaux derivativeIn mathematics, the Gâteaux differential or Gâteaux derivative is a generalization of the concept of directional derivative in differential calculus. Named after René Gâteaux, a French mathematician who died young in World War I, it is defined for functions between locally convex topological vector...
on more general locally convex spaces. Note that the well-known Hilbert spaceHilbert spaceThe mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
s are special cases of Banach spaceBanach spaceIn mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
s. The more formal treatment allows many theorems from ordinary calculusCalculusCalculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
and analysisMathematical analysisMathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
to be generalized to corresponding theorems in functional analysisFunctional analysisFunctional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
, as well as numerous new theorems to be stated.
Using the delta function as a test function
The definition given above is based on a relationship that holds for all test functions f, so one might think that it should hold also when f is chosen to be a specific function as the delta functionDirac delta functionThe Dirac delta function, or δ function, is a generalized function depending on a real parameter such that it is zero for all values of the parameter except when the parameter is zero, and its integral over the parameter from −∞ to ∞ is equal to one. It was introduced by theoretical...
. However, the latter is not a valid test function.
In the definition, the functional derivative describes how the functional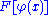 changes as a result of a small change in the entire function
changes as a result of a small change in the entire function 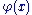 . The particular form of the change in
. The particular form of the change in 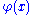 is not specified, but it should stretch over the whole interval on which
is not specified, but it should stretch over the whole interval on which  is defined. Employing the particular form of the perturbation given by the delta function has the meaning that
is defined. Employing the particular form of the perturbation given by the delta function has the meaning that 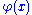 is varied only in the point
is varied only in the point 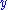 . Except for this point, there is no variation in
. Except for this point, there is no variation in 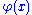 .
.
Often a physicist wants to know how one quantity, say the electric potential at position
at position 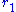 , is affected by changing another quantity, say the density of electric charge
, is affected by changing another quantity, say the density of electric charge 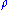 at position
at position 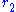 . The potential at a given position is a functional of the density, that is, given a particular density function and a point in space, one can compute a number which represents the potential of that point in space due to the specified density function. Since we are interested in how this number varies across all points in space, we treat the potential as a function of
. The potential at a given position is a functional of the density, that is, given a particular density function and a point in space, one can compute a number which represents the potential of that point in space due to the specified density function. Since we are interested in how this number varies across all points in space, we treat the potential as a function of  . To wit,
. To wit,

That is, for each , the potential
, the potential  is a functional of
is a functional of 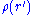 . Applying the definition of functional derivative,
. Applying the definition of functional derivative,
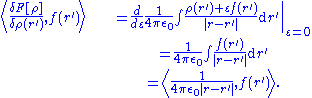
So,
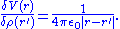
Now we can evaluate the functional derivative at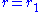 and
and  to see how the potential at
to see how the potential at  is changed due to a small variation in the density at
is changed due to a small variation in the density at 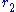 , but in general the unevaluated form is probably more useful.
, but in general the unevaluated form is probably more useful.
Examples
We give a formula to derive a common class of functionals that can be written as the integral of a function and its derivatives. This is a generalization of the Euler–Lagrange equation: indeed, the functional derivative was introduced in physicsPhysicsPhysics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
within the derivation of the Lagrange equation of the second kind from the principle of least actionPrinciple of least actionIn physics, the principle of least action – or, more accurately, the principle of stationary action – is a variational principle that, when applied to the action of a mechanical system, can be used to obtain the equations of motion for that system...
in Lagrangian mechanicsLagrangian mechanicsLagrangian mechanics is a re-formulation of classical mechanics that combines conservation of momentum with conservation of energy. It was introduced by the Italian-French mathematician Joseph-Louis Lagrange in 1788....
(18th century). The first three examples below are taken from density functional theoryDensity functional theoryDensity functional theory is a quantum mechanical modelling method used in physics and chemistry to investigate the electronic structure of many-body systems, in particular atoms, molecules, and the condensed phases. With this theory, the properties of a many-electron system can be determined by...
(20th century), the fourth from statistical mechanicsStatistical mechanicsStatistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
(19th century).
Formula for the integral of a function and its derivatives
Given a functional of the form
with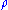 vanishing at the boundaries of
vanishing at the boundaries of  , the scalar product of the functional derivative with a function
, the scalar product of the functional derivative with a function  can be written
can be written
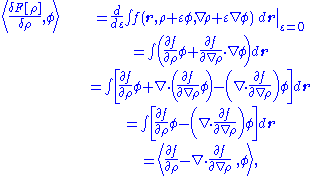
where, in the third line, is assumed at the integration boundaries. Thus the functional derivative is
is assumed at the integration boundaries. Thus the functional derivative is
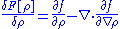
or, writing the expression more explicitly,

The above example is specific to the particular case that the functional depends on the function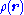 and its gradientGradientIn vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
and its gradientGradientIn vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
 only. In the more general case that the functional depends on higher order derivatives, i.e.
only. In the more general case that the functional depends on higher order derivatives, i.e.

where is a tensor whose
is a tensor whose 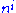 components
components 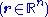 are all partial derivative operators of order
are all partial derivative operators of order  , i.e.
, i.e. 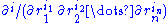 with
with  , an analogous application of the definition yields
, an analogous application of the definition yields
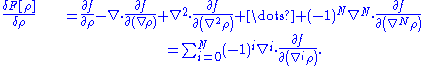
Thomas-Fermi kinetic energy functional
The Thomas-Fermi modelThomas-Fermi modelThe Thomas–Fermi model, named after Llewellyn Thomas and Enrico Fermi, is a quantum mechanical theory for the electronic structure of many-body systems developed semiclassically shortly after the introduction of the Schrödinger equation...
of 1927 used a kinetic energy functional for a noninteracting uniform electron gasFree electron modelIn solid-state physics, the free electron model is a simple model for the behaviour of valence electrons in a crystal structure of a metallic solid. It was developed principally by Arnold Sommerfeld who combined the classical Drude model with quantum mechanical Fermi-Dirac statistics and hence it...
in a first attempt of density-functional theory of electronic structure: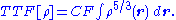
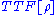 depends only on the charge density
depends only on the charge density  and does not depend on its gradient, Laplacian, or other higher-order derivatives (functionals like this are called “local”). Therefore,
and does not depend on its gradient, Laplacian, or other higher-order derivatives (functionals like this are called “local”). Therefore,
Coulomb potential energy functional
For the classical part of the potential, Thomas and Fermi employed the CoulombCoulomb's lawCoulomb's law or Coulomb's inverse-square law, is a law of physics describing the electrostatic interaction between electrically charged particles. It was first published in 1785 by French physicist Charles Augustin de Coulomb and was essential to the development of the theory of electromagnetism...
potential energy functional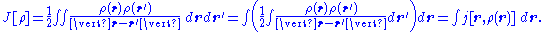
Again,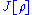 depends only on the charge density
depends only on the charge density 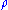 and does not depend on its gradient, Laplacian, or other higher-order derivatives (i.e., it is a “local” functional). Therefore,
and does not depend on its gradient, Laplacian, or other higher-order derivatives (i.e., it is a “local” functional). Therefore,
The second functional derivative of the Coulomb potential energy functional is
Weizsäcker kinetic energy functional
In 1935 von WeizsäckerCarl Friedrich von WeizsäckerCarl Friedrich Freiherr von Weizsäcker was a German physicist and philosopher. He was the longest-living member of the research team which performed nuclear research in Germany during the Second World War, under Werner Heisenberg's leadership...
proposed to add a gradient correction to the Thomas-Fermi kinetic energy functional to make it suit better a molecular electron cloud: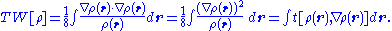
Now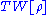 depends on the charge density
depends on the charge density 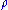 and its gradient
and its gradient 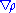 , therefore
, therefore
Writing a function as a functional
Finally, note that any function can be written in terms of an integral functional. For example,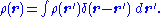
This functional depends on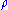 only, as the first two examples above (i.e., they are all “local”). Therefore,
only, as the first two examples above (i.e., they are all “local”). Therefore,
Entropy
The entropyInformation entropyIn information theory, entropy is a measure of the uncertainty associated with a random variable. In this context, the term usually refers to the Shannon entropy, which quantifies the expected value of the information contained in a message, usually in units such as bits...
of a discrete random variableRandom variableIn probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
is a functional of the probability mass functionProbability mass functionIn probability theory and statistics, a probability mass function is a function that gives the probability that a discrete random variable is exactly equal to some value...
.

Thus,

Thus,
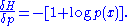
Exponential
Let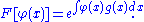
Using the delta function as a test function,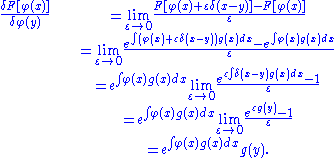
Thus,

