
Stiefel manifold
Encyclopedia
In mathematics
, the Stiefel manifold Vk(Rn) is the set of all orthonormal k-frames
in Rn. That is, it is the set of ordered k-tuples of orthonormal vectors in Rn. It is named after Swiss mathematician Eduard Stiefel
. Likewise one can define the complex
Stiefel manifold Vk(Cn) of orthonormal k-frames in Cn and the quaternion
ic Stiefel manifold Vk(Hn) of orthonormal k-frames in Hn. More generally, the construction applies to any real, complex, or quaternionic inner product space
.
In some contexts, a non-compact
Stiefel manifold is defined as the set of all linearly independent k-frames in Rn, Cn, or Hn; this is homotopy equivalent, as the compact Stiefel manifold is a deformation retract
of the non-compact one, by Gram–Schmidt
. Statements about the non-compact form correspond to those for the compact form, replacing the orthogonal group (or unitary or symplectic group) with the general linear group
.
by writing a k-frame as a matrix of k column vectors in Fn. The orthonormality condition is expressed by A*A = 1 where A* denotes the conjugate transpose
of A and 1 denotes the k × k identity matrix
. We then have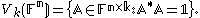
The topology on Vk(Fn) is the subspace topology
inherited from Fn×k. With this topology Vk(Fn) is a compact
manifold
whose dimension is given by
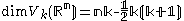
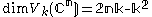

for the action
of a classical group
in a natural manner.
Every orthogonal transformation of a k-frame in Rn results in another k-frame, and any two k-frames are related by some orthogonal transformation. In other words, the orthogonal group
O(n) acts transitively on Vk(Rn). The stabilizer subgroup of a given frame is the subgroup isomorphic to O(n−k) which acts nontrivially on the orthogonal complement of the space spanned by that frame.
Likewise the unitary group
U(n) acts transitively on Vk(Cn) with stabilizer subgroup U(n−k) and the symplectic group
Sp(n) acts transitively on Vk(Hn) with stabilizer subgroup Sp(n−k).
In each case Vk(Fn) can be viewed as a homogeneous space:
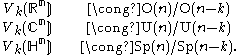
When k = n, the corresponding action is free so that the Stiefel manifold Vn(Fn) is a principal homogeneous space
for the corresponding classical group.
When k is strictly less than n then the special orthogonal group SO(n) also acts transitively on Vk(Rn) with stabilizer subgroup isomorphic to SO(n−k) so that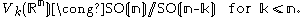
The same holds for the action of the special unitary group
on Vk(Cn)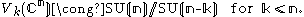
Thus for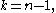 the Stiefel manifold is a principal homogeneous space for the corresponding special classical group.
the Stiefel manifold is a principal homogeneous space for the corresponding special classical group.
A 1-frame in Fn is nothing but a unit vector, so the Stiefel manifold V1(Fn) is just the unit sphere
in Fn.
Given a 2-frame in Rn, let the first vector define a point in Sn−1 and the second a unit tangent vector
to the sphere at that point. In this way, the Stiefel manifold V2(Rn) may be identified with the unit tangent bundle
to Sn−1.
When k = n or n−1 we saw in the previous section that Vk(Fn) is a principal homogeneous space, and therefore diffeomorphic to the corresponding classical group. These are listed in the table at the right.
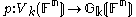
from the Stiefel manifold Vk(Fn) to the Grassmannian
of k-planes in Fn which sends a k-frame to the subspace
spanned by that frame. The fiber over a given point P in Gk(Fn) is the set of all orthonormal k-frames contained in the space P.
This projection has the structure of a principal G-bundle
where G is the associated classical group of degree k. Take the real case for concreteness. There is a natural right action of O(k) on Vk(Rn) which rotates a k-frame in the space it spans. This action is free but not transitive. The orbits of this action are precisely the orthonormal k-frames spanning a given k-dimensional subspace; that is, they are the fibers of the map p. Similar arguments hold in the complex and quaternionic cases.
We then have a sequence of principal bundles:
The vector bundle
s associated
to these principal bundles via the natural action of G on Fk are just the tautological bundle
s over the Grassmannians. In other words, the Stiefel manifold Vk(Fn) is the orthogonal, unitary, or symplectic frame bundle
associated to the tautological bundle on a Grassmannian.
When one passes to the n → ∞ limit, these bundles become the universal bundle
s for the classical groups.
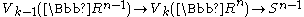 , thus the first non-trivial homotopy group
, thus the first non-trivial homotopy group
of the space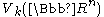 is in dimension
is in dimension  . Moreover,
. Moreover, 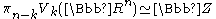 if
if 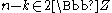 or if
or if 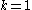 .
. 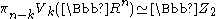 if
if  is odd and
is odd and  . This result is used in the obstruction-theoretic definition of Stiefel-Whitney classes.
. This result is used in the obstruction-theoretic definition of Stiefel-Whitney classes.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Stiefel manifold Vk(Rn) is the set of all orthonormal k-frames
K-frame
In linear algebra, a branch of mathematics, a k-frame is an ordered set of k linearly independent vectors in a space; thus k ≤ n, where n is the dimension of the vector space, and if k = n an n-frame is precisely an ordered basis.If the vectors are orthogonal, or orthonormal,...
in Rn. That is, it is the set of ordered k-tuples of orthonormal vectors in Rn. It is named after Swiss mathematician Eduard Stiefel
Eduard Stiefel
Eduard L. Stiefel was a Swiss mathematician. Together with Cornelius Lanczos and Magnus Hestenes, he invented the conjugate gradient method, and gave what is now understood to be a partial construction of the Stiefel–Whitney classes of a real vector bundle, thus co-founding the study of...
. Likewise one can define the complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
Stiefel manifold Vk(Cn) of orthonormal k-frames in Cn and the quaternion
Quaternion
In mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
ic Stiefel manifold Vk(Hn) of orthonormal k-frames in Hn. More generally, the construction applies to any real, complex, or quaternionic inner product space
Inner product space
In mathematics, an inner product space is a vector space with an additional structure called an inner product. This additional structure associates each pair of vectors in the space with a scalar quantity known as the inner product of the vectors...
.
In some contexts, a non-compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
Stiefel manifold is defined as the set of all linearly independent k-frames in Rn, Cn, or Hn; this is homotopy equivalent, as the compact Stiefel manifold is a deformation retract
Deformation retract
In topology, a branch of mathematics, a retraction , as the name suggests, "retracts" an entire space into a subspace. A deformation retraction is a map which captures the idea of continuously shrinking a space into a subspace.- Retract :...
of the non-compact one, by Gram–Schmidt
Gram–Schmidt process
In mathematics, particularly linear algebra and numerical analysis, the Gram–Schmidt process is a method for orthonormalising a set of vectors in an inner product space, most commonly the Euclidean space Rn...
. Statements about the non-compact form correspond to those for the compact form, replacing the orthogonal group (or unitary or symplectic group) with the general linear group
General linear group
In mathematics, the general linear group of degree n is the set of n×n invertible matrices, together with the operation of ordinary matrix multiplication. This forms a group, because the product of two invertible matrices is again invertible, and the inverse of an invertible matrix is invertible...
.
Topology
Let F stand for R, C, or H. The Stiefel manifold Vk(Fn) can be thought of as a set of n × k matricesMatrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
by writing a k-frame as a matrix of k column vectors in Fn. The orthonormality condition is expressed by A*A = 1 where A* denotes the conjugate transpose
Conjugate transpose
In mathematics, the conjugate transpose, Hermitian transpose, Hermitian conjugate, or adjoint matrix of an m-by-n matrix A with complex entries is the n-by-m matrix A* obtained from A by taking the transpose and then taking the complex conjugate of each entry...
of A and 1 denotes the k × k identity matrix
Identity matrix
In linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
. We then have
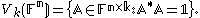
The topology on Vk(Fn) is the subspace topology
Subspace topology
In topology and related areas of mathematics, a subspace of a topological space X is a subset S of X which is equipped with a natural topology induced from that of X called the subspace topology .- Definition :Given a topological space and a subset S of X, the...
inherited from Fn×k. With this topology Vk(Fn) is a compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
whose dimension is given by
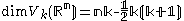

As a homogeneous space
Each of the Stiefel manifolds Vk(Fn) can be viewed as a homogeneous spaceHomogeneous space
In mathematics, particularly in the theories of Lie groups, algebraic groups and topological groups, a homogeneous space for a group G is a non-empty manifold or topological space X on which G acts continuously by symmetry in a transitive way. A special case of this is when the topological group,...
for the action
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
of a classical group
Classical group
In mathematics, the classical Lie groups are four infinite families of Lie groups closely related to the symmetries of Euclidean spaces. Their finite analogues are the classical groups of Lie type...
in a natural manner.
Every orthogonal transformation of a k-frame in Rn results in another k-frame, and any two k-frames are related by some orthogonal transformation. In other words, the orthogonal group
Orthogonal group
In mathematics, the orthogonal group of degree n over a field F is the group of n × n orthogonal matrices with entries from F, with the group operation of matrix multiplication...
O(n) acts transitively on Vk(Rn). The stabilizer subgroup of a given frame is the subgroup isomorphic to O(n−k) which acts nontrivially on the orthogonal complement of the space spanned by that frame.
Likewise the unitary group
Unitary group
In mathematics, the unitary group of degree n, denoted U, is the group of n×n unitary matrices, with the group operation that of matrix multiplication. The unitary group is a subgroup of the general linear group GL...
U(n) acts transitively on Vk(Cn) with stabilizer subgroup U(n−k) and the symplectic group
Symplectic group
In mathematics, the name symplectic group can refer to two different, but closely related, types of mathematical groups, denoted Sp and Sp. The latter is sometimes called the compact symplectic group to distinguish it from the former. Many authors prefer slightly different notations, usually...
Sp(n) acts transitively on Vk(Hn) with stabilizer subgroup Sp(n−k).
In each case Vk(Fn) can be viewed as a homogeneous space:
When k = n, the corresponding action is free so that the Stiefel manifold Vn(Fn) is a principal homogeneous space
Principal homogeneous space
In mathematics, a principal homogeneous space, or torsor, for a group G is a homogeneous space X for G such that the stabilizer subgroup of any point is trivial...
for the corresponding classical group.
When k is strictly less than n then the special orthogonal group SO(n) also acts transitively on Vk(Rn) with stabilizer subgroup isomorphic to SO(n−k) so that
The same holds for the action of the special unitary group
Special unitary group
The special unitary group of degree n, denoted SU, is the group of n×n unitary matrices with determinant 1. The group operation is that of matrix multiplication...
on Vk(Cn)
Thus for
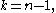 the Stiefel manifold is a principal homogeneous space for the corresponding special classical group.
the Stiefel manifold is a principal homogeneous space for the corresponding special classical group.Special cases
| k = 1 | 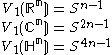 |
| k = n−1 | 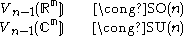 |
| k = n | 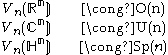 |
A 1-frame in Fn is nothing but a unit vector, so the Stiefel manifold V1(Fn) is just the unit sphere
Unit sphere
In mathematics, a unit sphere is the set of points of distance 1 from a fixed central point, where a generalized concept of distance may be used; a closed unit ball is the set of points of distance less than or equal to 1 from a fixed central point...
in Fn.
Given a 2-frame in Rn, let the first vector define a point in Sn−1 and the second a unit tangent vector
Tangent vector
A tangent vector is a vector that is tangent to a curve or surface at a given point.Tangent vectors are described in the differential geometry of curves in the context of curves in Rn. More generally, tangent vectors are elements of a tangent space of a differentiable manifold....
to the sphere at that point. In this way, the Stiefel manifold V2(Rn) may be identified with the unit tangent bundle
Unit tangent bundle
In Riemannian geometry, a branch of mathematics, the unit tangent bundle of a Riemannian manifold , denoted by UT or simply UTM, is the unit sphere bundle for the tangent bundle T...
to Sn−1.
When k = n or n−1 we saw in the previous section that Vk(Fn) is a principal homogeneous space, and therefore diffeomorphic to the corresponding classical group. These are listed in the table at the right.
As a principal bundle
There is a natural projection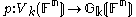
from the Stiefel manifold Vk(Fn) to the Grassmannian
Grassmannian
In mathematics, a Grassmannian is a space which parameterizes all linear subspaces of a vector space V of a given dimension. For example, the Grassmannian Gr is the space of lines through the origin in V, so it is the same as the projective space P. The Grassmanians are compact, topological...
of k-planes in Fn which sends a k-frame to the subspace
Linear subspace
The concept of a linear subspace is important in linear algebra and related fields of mathematics.A linear subspace is usually called simply a subspace when the context serves to distinguish it from other kinds of subspaces....
spanned by that frame. The fiber over a given point P in Gk(Fn) is the set of all orthonormal k-frames contained in the space P.
This projection has the structure of a principal G-bundle
Principal bundle
In mathematics, a principal bundle is a mathematical object which formalizes some of the essential features of the Cartesian product X × G of a space X with a group G...
where G is the associated classical group of degree k. Take the real case for concreteness. There is a natural right action of O(k) on Vk(Rn) which rotates a k-frame in the space it spans. This action is free but not transitive. The orbits of this action are precisely the orthonormal k-frames spanning a given k-dimensional subspace; that is, they are the fibers of the map p. Similar arguments hold in the complex and quaternionic cases.
We then have a sequence of principal bundles:

The vector bundle
Vector bundle
In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
s associated
Associated bundle
In mathematics, the theory of fiber bundles with a structure group G allows an operation of creating an associated bundle, in which the typical fiber of a bundle changes from F_1 to F_2, which are both topological spaces with a group action of G...
to these principal bundles via the natural action of G on Fk are just the tautological bundle
Tautological bundle
In mathematics, tautological bundle is a term for a particularly natural vector bundle occurring over a Grassmannian, and more specially over projective space...
s over the Grassmannians. In other words, the Stiefel manifold Vk(Fn) is the orthogonal, unitary, or symplectic frame bundle
Frame bundle
In mathematics, a frame bundle is a principal fiber bundle F associated to any vector bundle E. The fiber of F over a point x is the set of all ordered bases, or frames, for Ex...
associated to the tautological bundle on a Grassmannian.
When one passes to the n → ∞ limit, these bundles become the universal bundle
Universal bundle
In mathematics, the universal bundle in the theory of fiber bundles with structure group a given topological group G, is a specific bundle over a classifying space BG, such that every bundle with the given structure group G over M is a pullback by means of a continuous map-In the CW complex...
s for the classical groups.
Homotopy
The Stiefel manifolds fit into a family of fibrations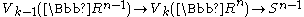 , thus the first non-trivial homotopy group
, thus the first non-trivial homotopy groupHomotopy group
In mathematics, homotopy groups are used in algebraic topology to classify topological spaces. The first and simplest homotopy group is the fundamental group, which records information about loops in a space...
of the space
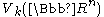 is in dimension
is in dimension  . Moreover,
. Moreover, 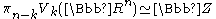 if
if 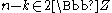 or if
or if 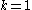 .
. 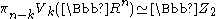 if
if  is odd and
is odd and  . This result is used in the obstruction-theoretic definition of Stiefel-Whitney classes.
. This result is used in the obstruction-theoretic definition of Stiefel-Whitney classes.External links
- Encyclopaedia of Mathematics » Stiefel manifold, Springer

