
Principal homogeneous space
Encyclopedia
In mathematics
, a principal homogeneous space, or torsor, for a group
G is a homogeneous space
X for G such that the stabilizer subgroup of any point is trivial. Equivalently, a principal homogeneous space for a group G is a set X on which G acts
freely and transitively, so that for any x, y in X there exists a unique g in G such that x·g = y where · denotes the (right) action of G on X.
An analogous definition holds in other categories
where, for example,
If G is nonabelian
then one must distinguish between left and right torsors according to whether the action is on the left or right. In this article, we will use right actions. To state the definition more explicitly, X is a G-torsor if X is nonempty and is equipped with a map (in the appropriate category) X × G → X such that
for all x ∈ X and all g,h ∈ G and such that the map X × G → X × X given by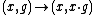
is an isomorphism (of sets, or topological spaces or ..., as appropriate). Note that this means that X and G are isomorphic. However — and this is the essential point —, there is no preferred 'identity' point in X. That is, X looks exactly like G but we have forgotten which point is the identity. This concept is often used in mathematics as a way of passing to a more intrinsic point of view, under the heading 'throw away the origin'.
Since X is not a group we cannot multiply elements; we can, however, take their "quotient". That is, there is a map X × X → G which sends (x,y) to the unique element g = x \ y ∈ G such that y = x·g.
The composition of this operation with the right group action, however, yields a ternary operation
X × (X × X) → X × G → X that serves as an affine generalization of group multiplication and is sufficient to both characterize a principal homogeneous space algebraically, and intrinsically characterize the group it is associated with. If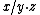 is the result of this operation, then the following identities
is the result of this operation, then the following identities
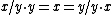
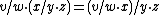
will suffice to define a principal homogeneous space, while the additional property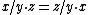
identifies those spaces that are associated with abelian groups. The group may be defined as formal quotients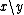 subject to the equivalence relation
subject to the equivalence relation ,
,
with the group product, identity and inverse defined, respectively, by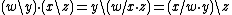 ,
,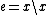 ,
,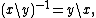
and the group action by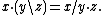
Another example is the affine space
concept: the idea of the affine space A underlying a vector space
V can be said succinctly by saying that A is principal homogeneous space for V acting as the additive group of translations.
Given a vector space
V we can take G to be the general linear group
GL(V), and X to be the set of all (ordered) bases
of V. Then G acts on X in the way that it acts on vectors of V; and it acts transitively
since any basis can be transformed via G to any other. What is more, a linear transformation fixing each vector of a basis will fix all v in V, hence being the neutral element of the general linear group GL(V) : so that X is indeed a principal homogeneous space. One way to follow basis-dependence in a linear algebra
argument is to track variables x in X. Similarly, the space of orthonormal bases (the Stiefel manifold
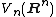 of n-frames
of n-frames
) is a principal homogeneous space for the orthogonal group
.
In category theory
, if two objects X and Y are isomorphic, then the isomorphisms between them, Iso(X,Y), form a torsor for the automorphism group of X, Aut(X), and likewise for Aut(Y); a choice of isomorphism between the objects gives an isomorphism between these groups and identifies the torsor with these two groups, and giving the torsor a group structure (as it is a base point).
: it means a principal bundle with base a single point. In other words the local theory of principal bundles is that of a family of principal homogeneous spaces depending on some parameters in the base. The 'origin' can be supplied by a section of the bundle—such sections are usually assumed to exist locally on the base—the bundle being locally trivial, so that the local structure is that of a cartesian product
. But sections will often not exist globally. For example a differential manifold M has a principal bundle of frames
associated to its tangent bundle
. A global section will exist (by definition) only when M is parallelizable, which implies strong topological restrictions.
In number theory
there is a (superficially different) reason to consider principal homogeneous spaces, for elliptic curve
s E defined over a field K (and more general abelian varieties
). Once this was understood various other examples were collected under the heading, for other algebraic group
s: quadratic form
s for orthogonal group
s, and Severi–Brauer varieties for projective linear group
s being two.
The reason of the interest for Diophantine equation
s, in the elliptic curve case, is that K may not be algebraically closed. There can exist curves C that have no point defined over K, and which become isomorphic over a larger field to E, which by definition has a point over K to serve as identity element for its addition law. That is, for this case we should distinguish C that have genus
1, from elliptic curves E that have a K-point (or, in other words, provide a Diophantine equation that has a solution in K). The curves C turn out to be torsors over E, and form a set carrying a rich structure in the case that K is a number field (the theory of the Selmer group). In fact a typical plane cubic curve C over Q has no particular reason to have a rational point; the standard Weierstrass model always does, namely the point at infinity, but you need a point over K to put C into that form over K.
This theory has been developed with great attention to local analysis
, leading to the definition of the Tate-Shafarevich group. In general the approach of taking the torsor theory, easy over an algebraically closed field
, and trying to get back 'down' to a smaller field is an aspect of descent
. It leads at once to questions of Galois cohomology
, since the torsors represent classes in group cohomology
H1.
/manifold
/topological space
etc.), and let G be a group over X, i.e., a group object
in the category
of spaces over X. In this case, a (right, say) G-torsor E on X is a space E (of the same type) over X with a (right) G action
such that the morphism

given by
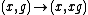
is an isomorphism
in the appropriate category
, and such that E is locally trivial on X, in that E→X acquires a section locally on X. Torsors in this sense correspond to classes in the cohomology
group H1(X,G).
When we are in the smooth manifold category
, then a G-torsor (for G a Lie group
) is then precisely a principal G-bundle
as defined above.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a principal homogeneous space, or torsor, for a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
G is a homogeneous space
Homogeneous space
In mathematics, particularly in the theories of Lie groups, algebraic groups and topological groups, a homogeneous space for a group G is a non-empty manifold or topological space X on which G acts continuously by symmetry in a transitive way. A special case of this is when the topological group,...
X for G such that the stabilizer subgroup of any point is trivial. Equivalently, a principal homogeneous space for a group G is a set X on which G acts
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
freely and transitively, so that for any x, y in X there exists a unique g in G such that x·g = y where · denotes the (right) action of G on X.
An analogous definition holds in other categories
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
where, for example,
- G is a topological groupTopological groupIn mathematics, a topological group is a group G together with a topology on G such that the group's binary operation and the group's inverse function are continuous functions with respect to the topology. A topological group is a mathematical object with both an algebraic structure and a...
, X is a topological spaceTopological spaceTopological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
and the action is continuous, - G is a Lie groupLie groupIn mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
, X is a smooth manifold and the action is smoothSmooth functionIn mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
, - G is an algebraic groupAlgebraic groupIn algebraic geometry, an algebraic group is a group that is an algebraic variety, such that the multiplication and inverse are given by regular functions on the variety...
, X is an algebraic varietyAlgebraic varietyIn mathematics, an algebraic variety is the set of solutions of a system of polynomial equations. Algebraic varieties are one of the central objects of study in algebraic geometry...
and the action is regularRegular functionIn mathematics, a regular function is a function that is analytic and single-valued in a given region. In complex analysis, any complex regular function is known as a holomorphic function...
.
If G is nonabelian
Nonabelian group
In mathematics, a non-abelian group, also sometimes called a non-commutative group, is a group in which there are at least two elements a and b of G such that a * b ≠ b * a...
then one must distinguish between left and right torsors according to whether the action is on the left or right. In this article, we will use right actions. To state the definition more explicitly, X is a G-torsor if X is nonempty and is equipped with a map (in the appropriate category) X × G → X such that
- x·1 = x
- x·(gh) = (x·g)·h
for all x ∈ X and all g,h ∈ G and such that the map X × G → X × X given by
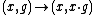
is an isomorphism (of sets, or topological spaces or ..., as appropriate). Note that this means that X and G are isomorphic. However — and this is the essential point —, there is no preferred 'identity' point in X. That is, X looks exactly like G but we have forgotten which point is the identity. This concept is often used in mathematics as a way of passing to a more intrinsic point of view, under the heading 'throw away the origin'.
Since X is not a group we cannot multiply elements; we can, however, take their "quotient". That is, there is a map X × X → G which sends (x,y) to the unique element g = x \ y ∈ G such that y = x·g.
The composition of this operation with the right group action, however, yields a ternary operation
Ternary operation
In mathematics, a ternary operation is an n-ary operation with n = 3. A ternary operation on a set A takes any given three elements of A and combines them to form a single element of A. An example of a ternary operation is the product in a heap....
X × (X × X) → X × G → X that serves as an affine generalization of group multiplication and is sufficient to both characterize a principal homogeneous space algebraically, and intrinsically characterize the group it is associated with. If
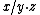 is the result of this operation, then the following identities
is the result of this operation, then the following identitiesIdentity (mathematics)
In mathematics, the term identity has several different important meanings:*An identity is a relation which is tautologically true. This means that whatever the number or value may be, the answer stays the same. For example, algebraically, this occurs if an equation is satisfied for all values of...
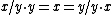
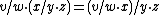
will suffice to define a principal homogeneous space, while the additional property
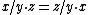
identifies those spaces that are associated with abelian groups. The group may be defined as formal quotients
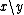 subject to the equivalence relation
subject to the equivalence relation ,
,with the group product, identity and inverse defined, respectively, by
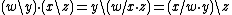 ,
,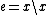 ,
,
and the group action by
Examples
Every group G can itself be thought of as a left or right G-torsor under the natural action of left or right multiplication.Another example is the affine space
Affine space
In mathematics, an affine space is a geometric structure that generalizes the affine properties of Euclidean space. In an affine space, one can subtract points to get vectors, or add a vector to a point to get another point, but one cannot add points. In particular, there is no distinguished point...
concept: the idea of the affine space A underlying a vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
V can be said succinctly by saying that A is principal homogeneous space for V acting as the additive group of translations.
Given a vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
V we can take G to be the general linear group
General linear group
In mathematics, the general linear group of degree n is the set of n×n invertible matrices, together with the operation of ordinary matrix multiplication. This forms a group, because the product of two invertible matrices is again invertible, and the inverse of an invertible matrix is invertible...
GL(V), and X to be the set of all (ordered) bases
Basis (linear algebra)
In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
of V. Then G acts on X in the way that it acts on vectors of V; and it acts transitively
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
since any basis can be transformed via G to any other. What is more, a linear transformation fixing each vector of a basis will fix all v in V, hence being the neutral element of the general linear group GL(V) : so that X is indeed a principal homogeneous space. One way to follow basis-dependence in a linear algebra
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
argument is to track variables x in X. Similarly, the space of orthonormal bases (the Stiefel manifold
Stiefel manifold
In mathematics, the Stiefel manifold Vk is the set of all orthonormal k-frames in Rn. That is, it is the set of ordered k-tuples of orthonormal vectors in Rn. It is named after Swiss mathematician Eduard Stiefel...
 of n-frames
of n-framesK-frame
In linear algebra, a branch of mathematics, a k-frame is an ordered set of k linearly independent vectors in a space; thus k ≤ n, where n is the dimension of the vector space, and if k = n an n-frame is precisely an ordered basis.If the vectors are orthogonal, or orthonormal,...
) is a principal homogeneous space for the orthogonal group
Orthogonal group
In mathematics, the orthogonal group of degree n over a field F is the group of n × n orthogonal matrices with entries from F, with the group operation of matrix multiplication...
.
In category theory
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
, if two objects X and Y are isomorphic, then the isomorphisms between them, Iso(X,Y), form a torsor for the automorphism group of X, Aut(X), and likewise for Aut(Y); a choice of isomorphism between the objects gives an isomorphism between these groups and identifies the torsor with these two groups, and giving the torsor a group structure (as it is a base point).
Applications
The principal homogeneous space concept is a special case of that of principal bundlePrincipal bundle
In mathematics, a principal bundle is a mathematical object which formalizes some of the essential features of the Cartesian product X × G of a space X with a group G...
: it means a principal bundle with base a single point. In other words the local theory of principal bundles is that of a family of principal homogeneous spaces depending on some parameters in the base. The 'origin' can be supplied by a section of the bundle—such sections are usually assumed to exist locally on the base—the bundle being locally trivial, so that the local structure is that of a cartesian product
Cartesian product
In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
. But sections will often not exist globally. For example a differential manifold M has a principal bundle of frames
Frame bundle
In mathematics, a frame bundle is a principal fiber bundle F associated to any vector bundle E. The fiber of F over a point x is the set of all ordered bases, or frames, for Ex...
associated to its tangent bundle
Tangent bundle
In differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...
. A global section will exist (by definition) only when M is parallelizable, which implies strong topological restrictions.
In number theory
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
there is a (superficially different) reason to consider principal homogeneous spaces, for elliptic curve
Elliptic curve
In mathematics, an elliptic curve is a smooth, projective algebraic curve of genus one, on which there is a specified point O. An elliptic curve is in fact an abelian variety — that is, it has a multiplication defined algebraically with respect to which it is a group — and O serves as the identity...
s E defined over a field K (and more general abelian varieties
Abelian variety
In mathematics, particularly in algebraic geometry, complex analysis and number theory, an abelian variety is a projective algebraic variety that is also an algebraic group, i.e., has a group law that can be defined by regular functions...
). Once this was understood various other examples were collected under the heading, for other algebraic group
Algebraic group
In algebraic geometry, an algebraic group is a group that is an algebraic variety, such that the multiplication and inverse are given by regular functions on the variety...
s: quadratic form
Quadratic form
In mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,4x^2 + 2xy - 3y^2\,\!is a quadratic form in the variables x and y....
s for orthogonal group
Orthogonal group
In mathematics, the orthogonal group of degree n over a field F is the group of n × n orthogonal matrices with entries from F, with the group operation of matrix multiplication...
s, and Severi–Brauer varieties for projective linear group
Projective linear group
In mathematics, especially in the group theoretic area of algebra, the projective linear group is the induced action of the general linear group of a vector space V on the associated projective space P...
s being two.
The reason of the interest for Diophantine equation
Diophantine equation
In mathematics, a Diophantine equation is an indeterminate polynomial equation that allows the variables to be integers only. Diophantine problems have fewer equations than unknown variables and involve finding integers that work correctly for all equations...
s, in the elliptic curve case, is that K may not be algebraically closed. There can exist curves C that have no point defined over K, and which become isomorphic over a larger field to E, which by definition has a point over K to serve as identity element for its addition law. That is, for this case we should distinguish C that have genus
Genus (mathematics)
In mathematics, genus has a few different, but closely related, meanings:-Orientable surface:The genus of a connected, orientable surface is an integer representing the maximum number of cuttings along non-intersecting closed simple curves without rendering the resultant manifold disconnected. It...
1, from elliptic curves E that have a K-point (or, in other words, provide a Diophantine equation that has a solution in K). The curves C turn out to be torsors over E, and form a set carrying a rich structure in the case that K is a number field (the theory of the Selmer group). In fact a typical plane cubic curve C over Q has no particular reason to have a rational point; the standard Weierstrass model always does, namely the point at infinity, but you need a point over K to put C into that form over K.
This theory has been developed with great attention to local analysis
Local analysis
In mathematics, the term local analysis has at least two meanings - both derived from the idea of looking at a problem relative to each prime number p first, and then later trying to integrate the information gained at each prime into a 'global' picture...
, leading to the definition of the Tate-Shafarevich group. In general the approach of taking the torsor theory, easy over an algebraically closed field
Algebraically closed field
In mathematics, a field F is said to be algebraically closed if every polynomial with one variable of degree at least 1, with coefficients in F, has a root in F.-Examples:...
, and trying to get back 'down' to a smaller field is an aspect of descent
Descent (category theory)
In mathematics, the idea of descent has come to stand for a very general idea, extending the intuitive idea of 'gluing' in topology. Since the topologists' glue is actually the use of equivalence relations on topological spaces, the theory starts with some ideas on identification.A sophisticated...
. It leads at once to questions of Galois cohomology
Galois cohomology
In mathematics, Galois cohomology is the study of the group cohomology of Galois modules, that is, the application of homological algebra to modules for Galois groups...
, since the torsors represent classes in group cohomology
Group cohomology
In abstract algebra, homological algebra, algebraic topology and algebraic number theory, as well as in applications to group theory proper, group cohomology is a way to study groups using a sequence of functors H n. The study of fixed points of groups acting on modules and quotient modules...
H1.
Other usage
The concept of a principal homogeneous space can also be globalized as follows. Let X be a "space" (a schemeScheme (mathematics)
In mathematics, a scheme is an important concept connecting the fields of algebraic geometry, commutative algebra and number theory. Schemes were introduced by Alexander Grothendieck so as to broaden the notion of algebraic variety; some consider schemes to be the basic object of study of modern...
/manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
/topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
etc.), and let G be a group over X, i.e., a group object
Group object
In category theory, a branch of mathematics, group objects are certain generalizations of groups which are built on more complicated structures than sets...
in the category
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
of spaces over X. In this case, a (right, say) G-torsor E on X is a space E (of the same type) over X with a (right) G action
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
such that the morphism

given by
is an isomorphism
Isomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
in the appropriate category
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
, and such that E is locally trivial on X, in that E→X acquires a section locally on X. Torsors in this sense correspond to classes in the cohomology
Cohomology
In mathematics, specifically in algebraic topology, cohomology is a general term for a sequence of abelian groups defined from a co-chain complex. That is, cohomology is defined as the abstract study of cochains, cocycles, and coboundaries...
group H1(X,G).
When we are in the smooth manifold category
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
, then a G-torsor (for G a Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
) is then precisely a principal G-bundle
Principal bundle
In mathematics, a principal bundle is a mathematical object which formalizes some of the essential features of the Cartesian product X × G of a space X with a group G...
as defined above.

