Gram–Schmidt process
Encyclopedia
In mathematics
, particularly linear algebra
and numerical analysis
, the Gram–Schmidt process is a method for orthonormalising
a set of vectors in an inner product space
, most commonly the Euclidean space
Rn. The Gram–Schmidt process takes a finite, linearly independent set S = {v1, …, vk} for and generates an orthogonal set that spans the same k-dimensional subspace of Rn as S.
The method is named for Jørgen Pedersen Gram
and Erhard Schmidt
but it appeared earlier in the work of Laplace and Cauchy. In the theory of Lie group decompositions
it is generalized by the Iwasawa decomposition
.
The application of the Gram–Schmidt process to the column vectors of a full column rank
matrix
yields the QR decomposition
(it is decomposed into an orthogonal
and a triangular matrix
).
operator by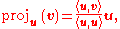
where 〈u, v〉 denotes the inner product of the vectors u and v. This operator projects the vector v orthogonally onto the vector u.
The Gram–Schmidt process then works as follows:
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, particularly linear algebra
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
and numerical analysis
Numerical analysis
Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
, the Gram–Schmidt process is a method for orthonormalising
Orthonormal basis
In mathematics, particularly linear algebra, an orthonormal basis for inner product space V with finite dimension is a basis for V whose vectors are orthonormal. For example, the standard basis for a Euclidean space Rn is an orthonormal basis, where the relevant inner product is the dot product of...
a set of vectors in an inner product space
Inner product space
In mathematics, an inner product space is a vector space with an additional structure called an inner product. This additional structure associates each pair of vectors in the space with a scalar quantity known as the inner product of the vectors...
, most commonly the Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
Rn. The Gram–Schmidt process takes a finite, linearly independent set S = {v1, …, vk} for and generates an orthogonal set that spans the same k-dimensional subspace of Rn as S.
The method is named for Jørgen Pedersen Gram
Jørgen Pedersen Gram
Jørgen Pedersen Gram was a Danish actuary and mathematician who was born in Nustrup, Duchy of Schleswig, Denmark and died in Copenhagen, Denmark....
and Erhard Schmidt
Erhard Schmidt
Erhard Schmidt was a German mathematician whose work significantly influenced the direction of mathematics in the twentieth century. He was born in Tartu, Governorate of Livonia . His advisor was David Hilbert and he was awarded his doctorate from Georg-August University of Göttingen in 1905...
but it appeared earlier in the work of Laplace and Cauchy. In the theory of Lie group decompositions
Lie group decompositions
In mathematics, Lie group decompositions, named after Sophus Lie, are used to analyse the structure of Lie groups and associated objects, by showing how they are built up out of subgroups. They are essential technical tools in the representation theory of Lie groups and Lie algebras; they can also...
it is generalized by the Iwasawa decomposition
Iwasawa decomposition
In mathematics, the Iwasawa decomposition KAN of a semisimple Lie group generalises the way a square real matrix can be written as a product of an orthogonal matrix and an upper triangular matrix...
.
The application of the Gram–Schmidt process to the column vectors of a full column rank
Rank (linear algebra)
The column rank of a matrix A is the maximum number of linearly independent column vectors of A. The row rank of a matrix A is the maximum number of linearly independent row vectors of A...
matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
yields the QR decomposition
QR decomposition
In linear algebra, a QR decomposition of a matrix is a decomposition of a matrix A into a product A=QR of an orthogonal matrix Q and an upper triangular matrix R...
(it is decomposed into an orthogonal
Orthogonal matrix
In linear algebra, an orthogonal matrix , is a square matrix with real entries whose columns and rows are orthogonal unit vectors ....
and a triangular matrix
Triangular matrix
In the mathematical discipline of linear algebra, a triangular matrix is a special kind of square matrix where either all the entries below or all the entries above the main diagonal are zero...
).
The Gram–Schmidt process
We define the projectionProjection (linear algebra)
In linear algebra and functional analysis, a projection is a linear transformation P from a vector space to itself such that P2 = P. It leaves its image unchanged....
operator by
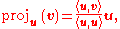
where 〈u, v〉 denotes the inner product of the vectors u and v. This operator projects the vector v orthogonally onto the vector u.
The Gram–Schmidt process then works as follows:
-
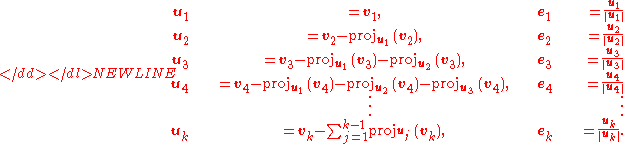
The sequence u1, ..., uk is the required system of orthogonal vectors, and the normalized vectors e1, ..., ek form an orthonormal set. The calculation of the sequence u1, ..., uk is known as Gram–Schmidt orthogonalization, while the calculation of the sequence e1, ..., ek is known as Gram–Schmidt orthonormalization as the vectors are normalized.
To check that these formulas yield an orthogonal sequence, first compute 〈u1, u2〉 by substituting the above formula for u2: we get zero. Then use this to compute 〈u1, u3〉 again by substituting the formula for u3: we get zero. The general proof proceeds by mathematical inductionMathematical inductionMathematical induction is a method of mathematical proof typically used to establish that a given statement is true of all natural numbers...
.
Geometrically, this method proceeds as follows: to compute ui, it projects vi orthogonally onto the subspace U generated by u1, ..., ui−1, which is the same as the subspace generated by v1, ..., vi−1. The vector ui is then defined to be the difference between vi and this projection, guaranteed to be orthogonal to all of the vectors in the subspace U.
The Gram–Schmidt process also applies to a linearly independent countably infinite sequence {vi}i. The result is an orthogonal (or orthonormal) sequence {ui}i such that for natural number n:
the algebraic span of v1, ..., vn is the same as that of u1, ..., un.
If the Gram–Schmidt process is applied to a linearly dependent sequence, it outputs the 0 vector on the ith step, assuming that vi is a linear combination of . If an orthonormal basis is to be produced, then the algorithm should test for zero vectors in the output and discard them because no multiple of a zero vector can have a length of 1. The number of vectors output by the algorithm will then be the dimension of the space spanned by the original inputs.
A variant of the Gram-Schmidt process using transfinite recursion applied to a (possibly uncountably) infinite sequence of vectors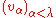
yields a set of orthonormal vectors 
with 
such that for any 
, the completion of the span of 
is the same as that of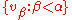 
. In particular, when applied to a (algebraic) basis of a Hilbert spaceHilbert spaceThe mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
(or, more generally, a basis of any dense subspace), it yields a (functional-analytic) orthonormal basis. Note that in the general case often the strict inequality
holds, even if the starting set was linearly independent, and the span of 
need not be a subspace of the span of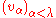 
(rather, it's a subspace of its completion).
Example
Consider the following set of vectors in R2 (with the conventional inner product)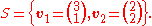
Now, perform Gram–Schmidt, to obtain an orthogonal set of vectors: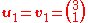
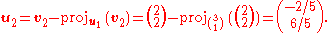
We check that the vectors u1 and u2 are indeed orthogonal: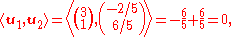
noting that if the dot product of two vectors is 0 then they are orthogonal.
We can then normalize the vectors by dividing out their sizes as shown above: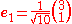
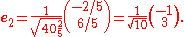
Numerical stability
When this process is implemented on a computer, the vectors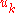
are often not quite orthogonal, due to rounding errorsRound-off errorA round-off error, also called rounding error, is the difference between the calculated approximation of a number and its exact mathematical value. Numerical analysis specifically tries to estimate this error when using approximation equations and/or algorithms, especially when using finitely many...
. For the Gram–Schmidt process as described above (sometimes referred to as "classical Gram–Schmidt") this loss of orthogonality is particularly bad; therefore, it is said that the (classical) Gram–Schmidt process is numerically unstableNumerical stabilityIn the mathematical subfield of numerical analysis, numerical stability is a desirable property of numerical algorithms. The precise definition of stability depends on the context, but it is related to the accuracy of the algorithm....
.
The Gram–Schmidt process can be stabilized by a small modification; this version is sometimes referred to as modified Gram-Schmidt or MGS.
This approach gives the same result as the original formula in exact arithmetic and introduces smaller errors in finite-precision arithmetic.
Instead of computing the vector uk as
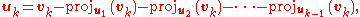
it is computed as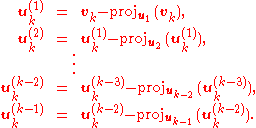
Each step finds a vector
orthogonal to 
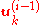. Thus 
is also orthogonalized against any errors introduced in computation of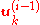 
.
Algorithm
The following algorithm implements the stabilized Gram–Schmidt orthonormalization. The vectors v1, …, vk are replaced by orthonormal vectors which span the same subspace.- for j from 1 to k do
- for i from 1 to j − 1 do
-
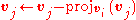(remove component in direction vi)
-
- next i
-
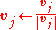(normalize)
- for i from 1 to j − 1 do
- next j
The cost of this algorithm is asymptotically 2nk2 floating point operations, where n is the dimensionality of the vectors .
Determinant formula
The result of the Gram–Schmidt process may be expressed in a non-recursive formula using determinantDeterminantIn linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
s.
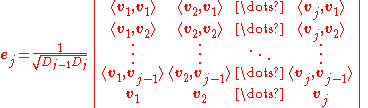
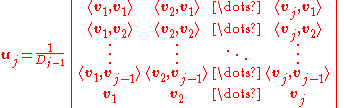
where D 0=1 and, for j ≥ 1, D j is the Gram determinant
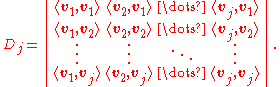
Note that the expression for uk is a "formal" determinant, i.e. the matrix contains both scalars
and vectors; the meaning of this expression is defined to be the result of a cofactor expansionLaplace expansionIn linear algebra, the Laplace expansion, named after Pierre-Simon Laplace, also called cofactor expansion, is an expression for the determinant |B| of...
along
the row of vectors.
The determinant formula for the Gram-Schmidt is computationally slower than the recursive algorithms described above;
it is mainly of theoretical interest.
Alternatives
Other orthogonalization algorithms use Householder transformationHouseholder transformationIn linear algebra, a Householder transformation is a linear transformation that describes a reflection about a plane or hyperplane containing the origin. Householder transformations are widely used in numerical linear algebra, to perform QR decompositions and in the first step of the QR algorithm...
s or Givens rotations. The algorithms using Householder transformations are more stable than the stabilized Gram–Schmidt process. On the other hand, the Gram–Schmidt process produces the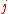
th orthogonalized vector after the 
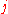th iteration, while orthogonalization using Householder reflections produces all the vectors only at the end. This makes only the Gram–Schmidt process applicable for iterative methodIterative methodIn computational mathematics, an iterative method is a mathematical procedure that generates a sequence of improving approximate solutions for a class of problems. A specific implementation of an iterative method, including the termination criteria, is an algorithm of the iterative method...
s like the Arnoldi iterationArnoldi iterationIn numerical linear algebra, the Arnoldi iteration is an eigenvalue algorithm and an important example of iterative methods. Arnoldi finds the eigenvalues of general matrices; an analogous method for Hermitian matrices is the Lanczos iteration. The Arnoldi iteration was invented by W. E...
.
Yet another alternative is motivated by the use of Cholesky decompositionCholesky decompositionIn linear algebra, the Cholesky decomposition or Cholesky triangle is a decomposition of a Hermitian, positive-definite matrix into the product of a lower triangular matrix and its conjugate transpose. It was discovered by André-Louis Cholesky for real matrices...
for inverting the matrix of the normal equations in linear least squares. Let
be a full column rank matrix, which columns need to be orthogonalized. The matrix 
is Hermitian and positive definite, so it can be written as 
using the Cholesky decompositionCholesky decompositionIn linear algebra, the Cholesky decomposition or Cholesky triangle is a decomposition of a Hermitian, positive-definite matrix into the product of a lower triangular matrix and its conjugate transpose. It was discovered by André-Louis Cholesky for real matrices...
. The lower triangular matrix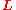
with strictly positive diagonal entries is invertible. Then columns of the matrix 
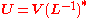are orthonormal and spanLinear spanIn the mathematical subfield of linear algebra, the linear span of a set of vectors in a vector space is the intersection of all subspaces containing that set...
the same subspace as the columns of the original matrix
. The explicit use of the product 
makes the algorithm unstable, especially if the product's condition numberCondition numberIn the field of numerical analysis, the condition number of a function with respect to an argument measures the asymptotically worst case of how much the function can change in proportion to small changes in the argument...
is large. Nevertheless, this algorithm is used in practice and implemented in some software packages because of its high efficiency and simplicity.
External links
- Harvey Mudd College Math Tutorial on the Gram-Schmidt algorithm
- Earliest known uses of some of the words of mathematics: G The entry "Gram-Schmidt orthogonalization" has some information and references on the origins of the method.
- Demos: Gram Schmidt process in plane and Gram Schmidt process in space
- Gram-Schmidt orthogonalization applet
- for j from 1 to k do