Scalar field theory
Encyclopedia
In theoretical physics
, scalar field theory can refer to a classical
or quantum theory
of scalar field
s. A field which is invariant under any Lorentz transformation
is called a "scalar", in contrast to a vector
or tensor field
. The quanta of the quantized scalar field are spin-zero particles, and as such are boson
s.
No fundamental scalar fields have been observed in nature, though the Higgs boson
may yet prove the first example. However, scalar fields appear in the effective field theory
descriptions of many physical phenomena. An example is the pion
, which is actually a "pseudoscalar", which means it is not invariant under parity transformations which invert the spatial directions, distinguishing it from a true scalar, which is parity-invariant. Because of the relative simplicity of the mathematics involved, scalar fields are often the first field introduced to a student of classical or quantum field theory.
In this article, the repeated index notation indicates the Einstein summation convention for summation over repeated indices. The theories described are defined in flat, D-dimensional Minkowski space
, with (D-1) spatial dimension and one time dimension and are, by construction, relativistically covariant. The Minkowski space metric
,
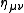, has a particularly simple form: it is diagonal
, and here we use the + − − −
sign convention
.
theory. The action
for the free relativistic
scalar field theory is
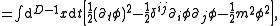
where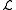
is known as a Lagrangian
density. This is an example of a quadratic action, since each of the terms is quadratic in the field,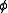
. The term proportional to 
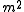is sometimes known as a mass term, due to its interpretation in the quantized version of this theory in terms of particle mass.
The equation of motion for this theory is obtained by extremizing the action above. It takes the following form, linear in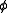
:
Note that this is the same as the Klein–Gordon equation, but that here the interpretation is as a classical field equation, rather than as a quantum mechanical wave equation.
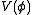to the equations of motion, where typically, V is a polynomial in φ of order 3 or more (often a monomial). Such a theory is sometimes said to be interacting
, because the Euler-Lagrange equation is now is nonlinear, implying a self-interaction
. The action for the most general such theory is
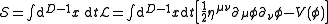
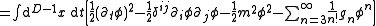
The n! factors in the expansion are introduced because they are useful in the Feynman diagram expansion of the quantum theory, as described below. The corresponding Euler-Lagrange equation of motion is
.
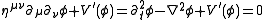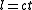, by using the velocity of light, c.
Similarly, any length l is equivalent to an inverse mass,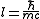
, using Planck's constant, 
. Heuristically, one can think of a time as a length, or either time or length as an inverse mass. In short, one can think of the dimensions of any physical quantity as defined in terms of just one independent dimension, rather than in terms of all three. This is most often termed the mass dimension
of the quantity.
One objection is that this theory is classical, and therefore it is not obvious that Planck's constant should be a part of the theory at all. In a sense this is a valid objection, and if desired one can indeed recast the theory without mass dimensions at all. However, this would be at the expense of making the connection with the quantum scalar field slightly more obscure. Given that one has dimensions of mass, Planck's constant is thought of here as an essentially arbitrary fixed quantity with dimensions appropriate to convert between mass and inverse length. This is consistent with the Feynman path integral approach to quantization, where the only reason for Planck's constant to appear stems from the same type of dimensional argument, since the action must be divided by some parameter with these dimensions to render the phase dimensionless.
, or mass dimension,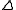
, of 
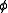describes the transformation of the field under a rescaling of coordinates:
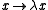
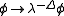
The units of action are the same as the units of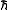
, and so the action itself has zero mass dimension. This fixes the scaling dimension of 
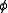to be
.
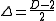. While the actions above are all constructed to have zero mass dimension, not all actions are invariant under the scaling transformation
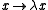
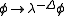
The reason that not all actions are invariant is that one usually thinks of the parameters m and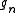
as fixed quantities, which are not rescaled under the transformation above. The condition for a scalar field theory to be scale invariant is then quite obvious: all of the parameters appearing in the action should be dimensionless quantities. In other words, a scale invariant theory is one without any fixed length scale (or equivalently, mass scale) in the theory.
For a scalar field theory with D spacetime dimensions, the only dimensionless parameter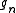
satisfies 
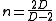. For example, in D=4 only 
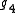is classically dimensionless, and so the only classically scale-invariant scalar field theory in 
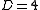is the massless 
theory. Classical scale invariance normally does not imply quantum scale invariance. See the discussion of the beta function below.
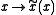
is said to be conformal
if the transformation satisfies
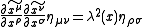
for some function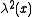
. The conformal group contains as subgroups the isometries
of the metric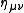
(the Poincaré group
) and also the scaling transformations (or dilatations) considered above. In fact, the scale-invariant theories in the previous section are also conformally-invariant.
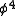theory illustrates a number of interesting phenomena in scalar field theory.
The Lagrangian density is
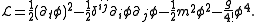
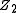symmetry under the transformation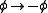 
This is an example of an internal symmetry, in contrast to a space-time symmetry
.
If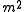
is positive, the potential 
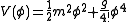has a single minimum, at the origin. The solution 
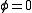is clearly invariant under the 
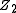symmetry. Conversely, if 
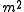is negative, then one can readily see that the potential 
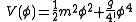has two minima. This is known as a double well potential, and the lowest energy states (known as the vacua, in quantum field theoretical language) in such a theory are not invariant under the 
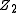symmetry of the action (in fact it maps each of the two vacua into the other). In this case, the 
symmetry is said to be spontaneously broken
.
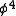theory with a negative 
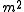also has a kink solution, which is a canonical example of a soliton
. Such a solution is of the form
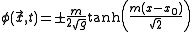
where x is one of the spatial variables (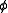
is taken to be independent of t, and the remaining spatial variables). The solution interpolates between the two different vacua of the double well potential. It is not possible to deform the kink into a constant solution without passing through a solution of infinite energy, and for this reason the kink is said to be stable. For 
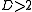, i.e. theories with more than one spatial dimension, this solution is called a domain wall
.
Another well-known example of a scalar field theory with kink solutions is the sine-Gordon theory.
rather than the real numbers. The action considered normally takes the form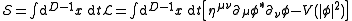
This has a U(1) symmetry, whose action on the space of fields rotates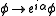
, for some real phase angle 
.
As for the real scalar field, spontaneous symmetry breaking is found if m2 is negative. This gives rise to a Mexican hat potential which is analogous to the double-well potential in real scalar
field theory, but now the choice of vacuum breaks a continuous U(1) symmetry instead of a discrete one.
This leads to a Goldstone boson
.
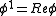and 
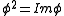which transform in the vector representation of the 
internal symmetry. Although such fields transform as a vector under the internal symmetry, they are still Lorentz scalars. This can be generalised to a theory of N scalar fields transforming in the vector representation of the O(N)
symmetry. The Lagrangian for an O(N)-invariant scalar field theory is typically of the form
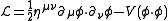
using an appropriate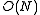
-invariant inner product.
, the fields, and all observables constructed from them, are replaced by quantum operators on a Hilbert space
. This Hilbert space is built on a vacuum state
, and dynamics are governed by a Hamiltonian
, a positive operator which annihilates the vacuum. A construction of a quantum scalar field theory may be found in the canonical quantization
article, which uses canonical commutation relations among the fields as a basis for the construction. In brief, the basic variables are the field φ and its canonical momentum π. Both fields are Hermitian. At spatial points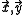
at equal times, the canonical commutation relations are given by
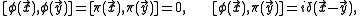
and the free Hamiltonian is
A spatial Fourier transform
leads to momentum space fields
which are used to define annihilation and creation operators
where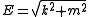
. These operators satisfy the commutation relations
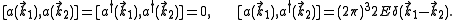
The state |0> annihilated by all of the operators a is identified as the bare vacuum, and a particle with momentum
is created by applying 
to the vacuum. Applying all possible combinations of creation operators to the vacuum constructs the Hilbert space. This construction is called Fock space
. The vacuum is annihilated by the Hamiltonian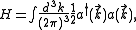
where the zero-point energy has been removed by Wick ordering. (See canonical quantization
.)
Interactions can be included by adding an interaction Hamiltonian. For a φ4 theory, this corresponds to adding a Wick ordered term g:φ4:/4! to the Hamiltonian, and integrating over x. Scattering amplitudes may be calculated from this Hamiltonian in the interaction picture
. These are constructed in perturbation theory
by means of the Dyson series
, which gives the time-ordered products, or n-particle Green's functions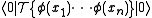
as described in the Dyson series
article. The Green's functions may also be obtained from a generating function that is constructed as a solution to the Schwinger-Dyson equation
.
expansion may be obtained also from the Feynman path integral formulation
. The time ordered vacuum expectation value
s of polynomials in φ, known as the n-particle Green's functions, are constructed by integrating over all possible fields, normalized by the vacuum expectation value
with no external fields,
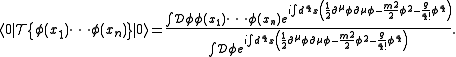
All of these Green's functions may be obtained by expanding the exponential in J(x)φ(x) in the generating function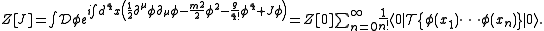
A Wick rotation
may be applied to make time imaginary. Changing the signature to (++++) then turns the Feynman integral into a statistical mechanics partition function
in Euclidean space
,
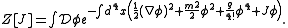
Normally, this is applied to the scattering of particles with fixed momenta, in which case, a Fourier transform
is useful, giving instead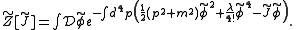
The standard trick to evaluate this functional integral is to write it as a product of exponential factors, schematically,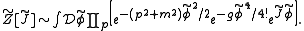
The second two exponential factors can be expanded as power series, and the combinatorics of this expansion can be represented graphically. The integral with λ = 0 can be treated as a product of infinitely many elementary Gaussian integrals, and the result may be expressed as a sum of Feynman diagrams, calculated using the following Feynman rules:
The last rule takes into account the effect of dividing by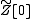
. The Minkowski-space Feynman rules are similar, except that each vertex is represented by -ig, while each internal line is represented by a propagator i/(q2-m2 + iε), where the 'ε term represents the small Wick rotation needed to make the Minkowski-space Gaussian integral converge.
, which is a procedure of adding divergent counter-terms to the Lagrangian in such a way that the diagrams constructed from the original Lagrangian and counter-terms is finite. A renormalization scale must be introduced in the process, and the coupling constant and mass become dependent upon it.
The dependence of a coupling constant g on the scale λ is encoded by
a beta function, β(g), defined by the relation
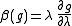
This dependence on the energy scale is known as the running of the coupling parameter, and theory of this kind of scale-dependence in quantum field theory is described by the renormalization group
.
Beta-functions are usually computed in an approximation scheme, most commonly perturbation theory
, where one assumes that the coupling constant is small. One can then make an expansion in powers of the coupling parameters and truncate the higher-order terms (also known as higher loop
contributions, due to the number of loops in the corresponding Feynman graph
s).
The beta-function at one loop (the first perturbative contribution) for the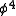
theory is
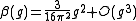
The fact that the sign in front of the lowest-order term is positive suggests that the coupling constant increases with energy. If this behavior persists at large couplings, this would indicate the presence of a Landau pole
at finite energy, or quantum triviality
. The question can only be answered non-perturbatively, since it involves strong coupling.
A quantum field theory is trivial when the running coupling, computed through its beta function, goes to zero when the cutoff is removed. Consequently, the propagator
becomes that of a free particle and the field is no longer interacting. Alternatively, the field theory may be interpreted as an effective theory, in which the cutoff is not removed, giving finite interactions but leading to a Landau pole
at some energy scale. For a φ4 interaction, Michael Aizenman
proved that the theory is indeed trivial for space-time dimension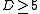
. For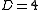 
the triviality has yet to be proven rigorously, but lattice computations have confirmed this. (See Landau pole
for details and references.) This fact is relevant as the Higgs field
, for which triviality bounds are used to set limits on the Higgs mass, based on the new physics must enter at a higher scale (perhaps the Planck scale
) to prevent the Landau pole from being reached.
Theoretical physics
Theoretical physics is a branch of physics which employs mathematical models and abstractions of physics to rationalize, explain and predict natural phenomena...
, scalar field theory can refer to a classical
Classical field theory
A classical field theory is a physical theory that describes the study of how one or more physical fields interact with matter. The word 'classical' is used in contrast to those field theories that incorporate quantum mechanics ....
or quantum theory
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
of scalar field
Scalar field
In mathematics and physics, a scalar field associates a scalar value to every point in a space. The scalar may either be a mathematical number, or a physical quantity. Scalar fields are required to be coordinate-independent, meaning that any two observers using the same units will agree on the...
s. A field which is invariant under any Lorentz transformation
Lorentz transformation
In physics, the Lorentz transformation or Lorentz-Fitzgerald transformation describes how, according to the theory of special relativity, two observers' varying measurements of space and time can be converted into each other's frames of reference. It is named after the Dutch physicist Hendrik...
is called a "scalar", in contrast to a vector
Vector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
or tensor field
Tensor field
In mathematics, physics and engineering, a tensor field assigns a tensor to each point of a mathematical space . Tensor fields are used in differential geometry, algebraic geometry, general relativity, in the analysis of stress and strain in materials, and in numerous applications in the physical...
. The quanta of the quantized scalar field are spin-zero particles, and as such are boson
Boson
In particle physics, bosons are subatomic particles that obey Bose–Einstein statistics. Several bosons can occupy the same quantum state. The word boson derives from the name of Satyendra Nath Bose....
s.
No fundamental scalar fields have been observed in nature, though the Higgs boson
Higgs boson
The Higgs boson is a hypothetical massive elementary particle that is predicted to exist by the Standard Model of particle physics. Its existence is postulated as a means of resolving inconsistencies in the Standard Model...
may yet prove the first example. However, scalar fields appear in the effective field theory
Effective field theory
In physics, an effective field theory is, as any effective theory, an approximate theory, that includes appropriate degrees of freedom to describe physical phenomena occurring at a chosen length scale, while ignoring substructure and degrees of freedom at shorter distances .-The renormalization...
descriptions of many physical phenomena. An example is the pion
Pion
In particle physics, a pion is any of three subatomic particles: , , and . Pions are the lightest mesons and they play an important role in explaining the low-energy properties of the strong nuclear force....
, which is actually a "pseudoscalar", which means it is not invariant under parity transformations which invert the spatial directions, distinguishing it from a true scalar, which is parity-invariant. Because of the relative simplicity of the mathematics involved, scalar fields are often the first field introduced to a student of classical or quantum field theory.
In this article, the repeated index notation indicates the Einstein summation convention for summation over repeated indices. The theories described are defined in flat, D-dimensional Minkowski space
Minkowski space
In physics and mathematics, Minkowski space or Minkowski spacetime is the mathematical setting in which Einstein's theory of special relativity is most conveniently formulated...
, with (D-1) spatial dimension and one time dimension and are, by construction, relativistically covariant. The Minkowski space metric
Metric (mathematics)
In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...
,
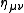, has a particularly simple form: it is diagonalDiagonal
A diagonal is a line joining two nonconsecutive vertices of a polygon or polyhedron. Informally, any sloping line is called diagonal. The word "diagonal" derives from the Greek διαγώνιος , from dia- and gonia ; it was used by both Strabo and Euclid to refer to a line connecting two vertices of a...
, and here we use the + − − −
Metric signature
The signature of a metric tensor is the number of positive and negative eigenvalues of the metric. That is, the corresponding real symmetric matrix is diagonalised, and the diagonal entries of each sign counted...
sign convention
Sign convention
In physics, a sign convention is a choice of the physical significance of signs for a set of quantities, in a case where the choice of sign is arbitrary. "Arbitrary" here means that the same physical system can be correctly described using different choices for the signs, as long as one set of...
.
Linear (free) theory
The most basic scalar field theory is the linearLinear
In mathematics, a linear map or function f is a function which satisfies the following two properties:* Additivity : f = f + f...
theory. The action
Action (physics)
In physics, action is an attribute of the dynamics of a physical system. It is a mathematical functional which takes the trajectory, also called path or history, of the system as its argument and has a real number as its result. Action has the dimension of energy × time, and its unit is...
for the free relativistic
Theory of relativity
The theory of relativity, or simply relativity, encompasses two theories of Albert Einstein: special relativity and general relativity. However, the word relativity is sometimes used in reference to Galilean invariance....
scalar field theory is
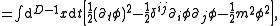
where
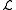is known as a LagrangianLagrangian
The Lagrangian, L, of a dynamical system is a function that summarizes the dynamics of the system. It is named after Joseph Louis Lagrange. The concept of a Lagrangian was originally introduced in a reformulation of classical mechanics by Irish mathematician William Rowan Hamilton known as...
density. This is an example of a quadratic action, since each of the terms is quadratic in the field,
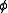. The term proportional to 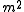is sometimes known as a mass term, due to its interpretation in the quantized version of this theory in terms of particle mass.The equation of motion for this theory is obtained by extremizing the action above. It takes the following form, linear in
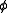:Note that this is the same as the Klein–Gordon equation, but that here the interpretation is as a classical field equation, rather than as a quantum mechanical wave equation.
Nonlinear (interacting) theory
The most common generalization of the linear theory above is to add a scalar potentialScalar potential
A scalar potential is a fundamental concept in vector analysis and physics . The scalar potential is an example of a scalar field...
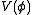to the equations of motion, where typically, V is a polynomial in φ of order 3 or more (often a monomial). Such a theory is sometimes said to be interactingInteraction
Interaction is a kind of action that occurs as two or more objects have an effect upon one another. The idea of a two-way effect is essential in the concept of interaction, as opposed to a one-way causal effect...
, because the Euler-Lagrange equation is now is nonlinear, implying a self-interaction
Self-energy
In theoretical physics and quantum field theory a particle's self-energy \Sigma represents the contribution to the particle's energy, or effective mass, due to interactions between the particle and the system it is part of...
. The action for the most general such theory is
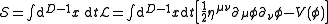
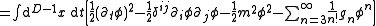
The n! factors in the expansion are introduced because they are useful in the Feynman diagram expansion of the quantum theory, as described below. The corresponding Euler-Lagrange equation of motion is
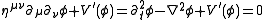.Dimensional analysis and scaling
Physical quantities in these scalar field theories may have dimensions of length, time or mass, or some combination of the three. However, in a relativistic theory, any quantity t, with dimensions of time, can be 'converted' into a length,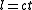, by using the velocity of light, c.Similarly, any length l is equivalent to an inverse mass,
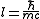, using Planck's constant, . Heuristically, one can think of a time as a length, or either time or length as an inverse mass. In short, one can think of the dimensions of any physical quantity as defined in terms of just one independent dimension, rather than in terms of all three. This is most often termed the mass dimensionClassical scaling dimension
In theoretical physics, namely quantum field theory, the classical scaling dimension of an operator O is the power of mass of an operator determined by dimensional analysis from the Lagrangian...
of the quantity.
One objection is that this theory is classical, and therefore it is not obvious that Planck's constant should be a part of the theory at all. In a sense this is a valid objection, and if desired one can indeed recast the theory without mass dimensions at all. However, this would be at the expense of making the connection with the quantum scalar field slightly more obscure. Given that one has dimensions of mass, Planck's constant is thought of here as an essentially arbitrary fixed quantity with dimensions appropriate to convert between mass and inverse length. This is consistent with the Feynman path integral approach to quantization, where the only reason for Planck's constant to appear stems from the same type of dimensional argument, since the action must be divided by some parameter with these dimensions to render the phase dimensionless.
Scaling Dimension
The classical scaling dimensionClassical scaling dimension
In theoretical physics, namely quantum field theory, the classical scaling dimension of an operator O is the power of mass of an operator determined by dimensional analysis from the Lagrangian...
, or mass dimension,
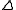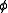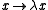
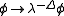
, of describes the transformation of the field under a rescaling of coordinates:The units of action are the same as the units of
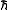, and so the action itself has zero mass dimension. This fixes the scaling dimension of 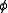to be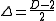.Scale invariance
There is a specific sense in which some scalar field theories are scale-invariantScale invariance
In physics and mathematics, scale invariance is a feature of objects or laws that do not change if scales of length, energy, or other variables, are multiplied by a common factor...
. While the actions above are all constructed to have zero mass dimension, not all actions are invariant under the scaling transformation
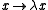
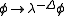
The reason that not all actions are invariant is that one usually thinks of the parameters m and
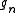as fixed quantities, which are not rescaled under the transformation above. The condition for a scalar field theory to be scale invariant is then quite obvious: all of the parameters appearing in the action should be dimensionless quantities. In other words, a scale invariant theory is one without any fixed length scale (or equivalently, mass scale) in the theory.For a scalar field theory with D spacetime dimensions, the only dimensionless parameter
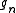satisfies 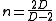. For example, in D=4 only 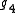is classically dimensionless, and so the only classically scale-invariant scalar field theory in 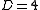is the massless theory. Classical scale invariance normally does not imply quantum scale invariance. See the discussion of the beta function below.Conformal invariance
A transformation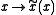is said to be conformal
Conformal symmetry
In theoretical physics, conformal symmetry is a symmetry under dilatation and under the special conformal transformations...
if the transformation satisfies
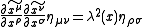
for some function
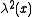. The conformal group contains as subgroups the isometriesIsometry
In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
of the metric
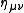(the Poincaré groupPoincaré group
In physics and mathematics, the Poincaré group, named after Henri Poincaré, is the group of isometries of Minkowski spacetime.-Simple explanation:...
) and also the scaling transformations (or dilatations) considered above. In fact, the scale-invariant theories in the previous section are also conformally-invariant.
φ4 theory
Massive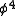 theory illustrates a number of interesting phenomena in scalar field theory.The Lagrangian density is
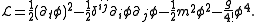
Spontaneous symmetry breaking
This Lagrangian has a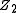 symmetry under the transformation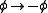 This is an example of an internal symmetry, in contrast to a space-time symmetry
Spacetime symmetries
Spacetime symmetries are features of spacetime that can be described as exhibiting some form of symmetry. The role of symmetry in physics is important in simplifying solutions to many problems, spacetime symmetries finding ample application in the study of exact solutions of Einstein's field...
.
If
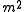is positive, the potential 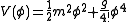has a single minimum, at the origin. The solution 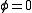is clearly invariant under the 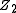symmetry. Conversely, if 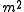is negative, then one can readily see that the potential 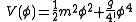has two minima. This is known as a double well potential, and the lowest energy states (known as the vacua, in quantum field theoretical language) in such a theory are not invariant under the 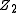symmetry of the action (in fact it maps each of the two vacua into the other). In this case, the symmetry is said to be spontaneously brokenSpontaneous symmetry breaking
Spontaneous symmetry breaking is the process by which a system described in a theoretically symmetrical way ends up in an apparently asymmetric state....
.
Kink solutions
The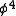 theory with a negative 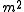also has a kink solution, which is a canonical example of a solitonSoliton
In mathematics and physics, a soliton is a self-reinforcing solitary wave that maintains its shape while it travels at constant speed. Solitons are caused by a cancellation of nonlinear and dispersive effects in the medium...
. Such a solution is of the form
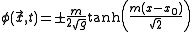
where x is one of the spatial variables (
is taken to be independent of t, and the remaining spatial variables). The solution interpolates between the two different vacua of the double well potential. It is not possible to deform the kink into a constant solution without passing through a solution of infinite energy, and for this reason the kink is said to be stable. For , i.e. theories with more than one spatial dimension, this solution is called a domain wallDomain wall
A domain wall is a term used in physics which can have one of two distinct but similar meanings in magnetism, optics, or string theory. These phenomena can all be generically described as topological solitons which occur whenever a discrete symmetry is spontaneously broken.-Magnetism:In magnetism,...
.
Another well-known example of a scalar field theory with kink solutions is the sine-Gordon theory.
Complex scalar field theory
In a complex scalar field theory, the scalar field takes values in the complex numbers,rather than the real numbers. The action considered normally takes the form
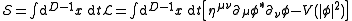
This has a U(1) symmetry, whose action on the space of fields rotates
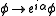, for some real phase angle .As for the real scalar field, spontaneous symmetry breaking is found if m2 is negative. This gives rise to a Mexican hat potential which is analogous to the double-well potential in real scalar
field theory, but now the choice of vacuum breaks a continuous U(1) symmetry instead of a discrete one.
This leads to a Goldstone boson
Goldstone boson
In particle and condensed matter physics, Goldstone bosons or Nambu–Goldstone bosons are bosons that appear necessarily in models exhibiting spontaneous breakdown of continuous symmetries...
.
O(N) theory
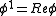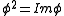One can express the complex scalar field theory in terms of two real fields, and which transform in the vector representation of the internal symmetry. Although such fields transform as a vector under the internal symmetry, they are still Lorentz scalars. This can be generalised to a theory of N scalar fields transforming in the vector representation of the O(N)Orthogonal group
In mathematics, the orthogonal group of degree n over a field F is the group of n × n orthogonal matrices with entries from F, with the group operation of matrix multiplication...
symmetry. The Lagrangian for an O(N)-invariant scalar field theory is typically of the form
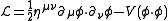
using an appropriate
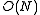-invariant inner product.Quantum scalar field theory
In quantum field theoryQuantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
, the fields, and all observables constructed from them, are replaced by quantum operators on a Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
. This Hilbert space is built on a vacuum state
Vacuum state
In quantum field theory, the vacuum state is the quantum state with the lowest possible energy. Generally, it contains no physical particles...
, and dynamics are governed by a Hamiltonian
Hamiltonian (quantum mechanics)
In quantum mechanics, the Hamiltonian H, also Ȟ or Ĥ, is the operator corresponding to the total energy of the system. Its spectrum is the set of possible outcomes when one measures the total energy of a system...
, a positive operator which annihilates the vacuum. A construction of a quantum scalar field theory may be found in the canonical quantization
Canonical quantization
In physics, canonical quantization is a procedure for quantizing a classical theory while attempting to preserve the formal structure of the classical theory, to the extent possible. Historically, this was Werner Heisenberg's route to obtaining quantum mechanics...
article, which uses canonical commutation relations among the fields as a basis for the construction. In brief, the basic variables are the field φ and its canonical momentum π. Both fields are Hermitian. At spatial points
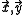at equal times, the canonical commutation relations are given by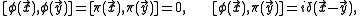and the free Hamiltonian is
A spatial Fourier transform
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
leads to momentum space fields
which are used to define annihilation and creation operators
where
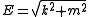. These operators satisfy the commutation relations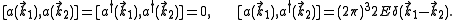The state |0> annihilated by all of the operators a is identified as the bare vacuum, and a particle with momentum
is created by applying to the vacuum. Applying all possible combinations of creation operators to the vacuum constructs the Hilbert space. This construction is called Fock spaceFock space
The Fock space is an algebraic system used in quantum mechanics to describe quantum states with a variable or unknown number of particles. It is named after V. A...
. The vacuum is annihilated by the Hamiltonian
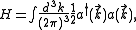
where the zero-point energy has been removed by Wick ordering. (See canonical quantization
Canonical quantization
In physics, canonical quantization is a procedure for quantizing a classical theory while attempting to preserve the formal structure of the classical theory, to the extent possible. Historically, this was Werner Heisenberg's route to obtaining quantum mechanics...
.)
Interactions can be included by adding an interaction Hamiltonian. For a φ4 theory, this corresponds to adding a Wick ordered term g:φ4:/4! to the Hamiltonian, and integrating over x. Scattering amplitudes may be calculated from this Hamiltonian in the interaction picture
Interaction picture
In quantum mechanics, the Interaction picture is an intermediate between the Schrödinger picture and the Heisenberg picture. Whereas in the other two pictures either the state vector or the operators carry time dependence, in the interaction picture both carry part of the time dependence of...
. These are constructed in perturbation theory
Perturbation theory (quantum mechanics)
In quantum mechanics, perturbation theory is a set of approximation schemes directly related to mathematical perturbation for describing a complicated quantum system in terms of a simpler one. The idea is to start with a simple system for which a mathematical solution is known, and add an...
by means of the Dyson series
Dyson series
In scattering theory, the Dyson series, formulated by British-born American physicist Freeman Dyson, is a perturbative series, and each term is represented by Feynman diagrams. This series diverges asymptotically, but in quantum electrodynamics at the second order the difference from...
, which gives the time-ordered products, or n-particle Green's functions
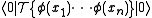as described in the Dyson seriesDyson series
In scattering theory, the Dyson series, formulated by British-born American physicist Freeman Dyson, is a perturbative series, and each term is represented by Feynman diagrams. This series diverges asymptotically, but in quantum electrodynamics at the second order the difference from...
article. The Green's functions may also be obtained from a generating function that is constructed as a solution to the Schwinger-Dyson equation
Schwinger-Dyson equation
The Schwinger–Dyson equation , also Dyson-Schwinger equations, named after Julian Schwinger and Freeman Dyson, are general relations between Green functions in quantum field theories...
.
Feynman Path Integral
The Feynman diagramFeynman diagram
Feynman diagrams are a pictorial representation scheme for the mathematical expressions governing the behavior of subatomic particles, first developed by the Nobel Prize-winning American physicist Richard Feynman, and first introduced in 1948...
expansion may be obtained also from the Feynman path integral formulation
Path integral formulation
The path integral formulation of quantum mechanics is a description of quantum theory which generalizes the action principle of classical mechanics...
. The time ordered vacuum expectation value
Vacuum expectation value
In quantum field theory the vacuum expectation value of an operator is its average, expected value in the vacuum. The vacuum expectation value of an operator O is usually denoted by \langle O\rangle...
s of polynomials in φ, known as the n-particle Green's functions, are constructed by integrating over all possible fields, normalized by the vacuum expectation value
Vacuum expectation value
In quantum field theory the vacuum expectation value of an operator is its average, expected value in the vacuum. The vacuum expectation value of an operator O is usually denoted by \langle O\rangle...
with no external fields,
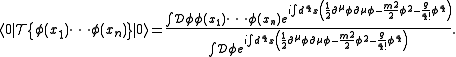
All of these Green's functions may be obtained by expanding the exponential in J(x)φ(x) in the generating function
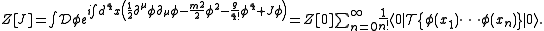
A Wick rotation
Wick rotation
In physics, Wick rotation, named after Gian-Carlo Wick, is a method of finding a solution to a mathematical problem in Minkowski space from a solution to a related problem in Euclidean space by means of a transformation that substitutes an imaginary-number variable for a real-number variable...
may be applied to make time imaginary. Changing the signature to (++++) then turns the Feynman integral into a statistical mechanics partition function
Partition function (statistical mechanics)
Partition functions describe the statistical properties of a system in thermodynamic equilibrium. It is a function of temperature and other parameters, such as the volume enclosing a gas...
in Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
,
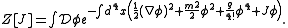
Normally, this is applied to the scattering of particles with fixed momenta, in which case, a Fourier transform
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
is useful, giving instead
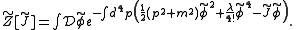
The standard trick to evaluate this functional integral is to write it as a product of exponential factors, schematically,
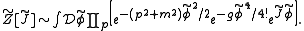
The second two exponential factors can be expanded as power series, and the combinatorics of this expansion can be represented graphically. The integral with λ = 0 can be treated as a product of infinitely many elementary Gaussian integrals, and the result may be expressed as a sum of Feynman diagrams, calculated using the following Feynman rules:
- Each field
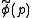in the n-point Euclidean Green's function is represented by an external line (half-edge) in the graph, and associated with momentum p. - Each vertex is represented by a factor -g.
- At a given order gk, all diagrams with n external lines and k vertices are constructed such that the momenta flowing into each vertex is zero. Each internal line is represented by a propagator 1/(q2 + m2), where q is the momentum flowing through that line.
- Any unconstrained momenta are integrated over all values.
- The result is divided by a symmetry factor, which is the number of ways the lines and vertices of the graph can be rearranged without changing its connectivity.
- Do not include graphs containing "vacuum bubbles", connected subgraphs with no external lines.
The last rule takes into account the effect of dividing by
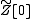. The Minkowski-space Feynman rules are similar, except that each vertex is represented by -ig, while each internal line is represented by a propagator i/(q2-m2 + iε), where the 'ε term represents the small Wick rotation needed to make the Minkowski-space Gaussian integral converge.Renormalization
The integrals over unconstrained momenta, called "loop integrals", in the Feynman graphs typically diverge. This is normally handled by renormalizationRenormalization
In quantum field theory, the statistical mechanics of fields, and the theory of self-similar geometric structures, renormalization is any of a collection of techniques used to treat infinities arising in calculated quantities....
, which is a procedure of adding divergent counter-terms to the Lagrangian in such a way that the diagrams constructed from the original Lagrangian and counter-terms is finite. A renormalization scale must be introduced in the process, and the coupling constant and mass become dependent upon it.
The dependence of a coupling constant g on the scale λ is encoded by
a beta function, β(g), defined by the relation
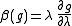
This dependence on the energy scale is known as the running of the coupling parameter, and theory of this kind of scale-dependence in quantum field theory is described by the renormalization group
Renormalization group
In theoretical physics, the renormalization group refers to a mathematical apparatus that allows systematic investigation of the changes of a physical system as viewed at different distance scales...
.
Beta-functions are usually computed in an approximation scheme, most commonly perturbation theory
Perturbation theory (quantum mechanics)
In quantum mechanics, perturbation theory is a set of approximation schemes directly related to mathematical perturbation for describing a complicated quantum system in terms of a simpler one. The idea is to start with a simple system for which a mathematical solution is known, and add an...
, where one assumes that the coupling constant is small. One can then make an expansion in powers of the coupling parameters and truncate the higher-order terms (also known as higher loop
Feynman graph
A Feynman graph is a graph suitable to be a Feynman diagram in a particular application of quantum field theory.A Feynman graph is a graph suitable to be a Feynman diagram in a particular application of quantum field theory.A Feynman graph is a graph suitable to be a Feynman diagram in a particular...
contributions, due to the number of loops in the corresponding Feynman graph
Feynman graph
A Feynman graph is a graph suitable to be a Feynman diagram in a particular application of quantum field theory.A Feynman graph is a graph suitable to be a Feynman diagram in a particular application of quantum field theory.A Feynman graph is a graph suitable to be a Feynman diagram in a particular...
s).
The beta-function at one loop (the first perturbative contribution) for the
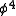theory is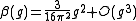The fact that the sign in front of the lowest-order term is positive suggests that the coupling constant increases with energy. If this behavior persists at large couplings, this would indicate the presence of a Landau pole
Landau pole
In physics, the Landau pole is the momentum scale at which the coupling constant of a quantum field theory becomes infinite...
at finite energy, or quantum triviality
Quantum triviality
In a quantum field theory, charge screening can restrict the value of the observable "renormalized" charge of a classical theory. Ifthe only allowed value of the renormalized charge is zero, the theory is said to be "trivial" or noninteracting...
. The question can only be answered non-perturbatively, since it involves strong coupling.
A quantum field theory is trivial when the running coupling, computed through its beta function, goes to zero when the cutoff is removed. Consequently, the propagator
Propagator
In quantum mechanics and quantum field theory, the propagator gives the probability amplitude for a particle to travel from one place to another in a given time, or to travel with a certain energy and momentum. Propagators are used to represent the contribution of virtual particles on the internal...
becomes that of a free particle and the field is no longer interacting. Alternatively, the field theory may be interpreted as an effective theory, in which the cutoff is not removed, giving finite interactions but leading to a Landau pole
Landau pole
In physics, the Landau pole is the momentum scale at which the coupling constant of a quantum field theory becomes infinite...
at some energy scale. For a φ4 interaction, Michael Aizenman
Michael Aizenman
Michael Aizenman is a mathematician and a physicist at Princeton University working in the fields of mathematical physics, statistical mechanics, functional analysis and probability theory....
proved that the theory is indeed trivial for space-time dimension
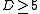. For 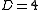the triviality has yet to be proven rigorously, but lattice computations have confirmed this. (See Landau poleLandau pole
In physics, the Landau pole is the momentum scale at which the coupling constant of a quantum field theory becomes infinite...
for details and references.) This fact is relevant as the Higgs field
Higgs mechanism
In particle physics, the Higgs mechanism is the process in which gauge bosons in a gauge theory can acquire non-vanishing masses through absorption of Nambu-Goldstone bosons arising in spontaneous symmetry breaking....
, for which triviality bounds are used to set limits on the Higgs mass, based on the new physics must enter at a higher scale (perhaps the Planck scale
Planck scale
In particle physics and physical cosmology, the Planck scale is an energy scale around 1.22 × 1019 GeV at which quantum effects of gravity become strong...
) to prevent the Landau pole from being reached.
Further reading
- Peskin, M and Schroeder, D. ;An Introduction to Quantum Field Theory, Westview Press (1995)
- Weinberg, Steven ; The Quantum Theory of Fields, (3 volumes) Cambridge University Press (1995)
- Srednicki, Mark; Quantum Field Theory, Cambridge University Press (2007)
- Zinn-Justin, Jean ; Quantum Field Theory and Critical Phenomena, Oxford University Press (2002)
External links
- Pedagogic Aides to Quantum Field Theory Click on the link for Chap. 3 to find an extensive, simplified introduction to scalars in relativistic quantum mechanics and quantum field theory.
- 't Hooft, G., "The Conceptual Basis of Quantum Field Theory" (online version).