
Feynman graph
Encyclopedia
A Feynman graph is a graph suitable to be a Feynman diagram
in a particular application of quantum field theory
.
(The most common use is when each field has quanta
(particles) associated with it - since the quantum of the electromagnetic field
is a photon
. For simplicity, we will discuss them in terms of that case. Those who would apply Feynman diagram
s in other subjects or categories should translate the explanation with an appropriate isomorphism
.)
A Feynman graph is a finite, partially directed
, colored pseudograph which satisfies certain conditions.("Pseudograph" means the graph
can have loops
and multiple edges; "partially directed" means, in general, some edges are directed and others are not). Each edge represents a segment of the world line
of a particle
. There are two kinds of vertex: External vertices represent single particles entering or exiting the reaction as a whole, and so they have degree
1. The color of an edge or an exterior vertex will represent the type of particle. Internal vertices represent interactions, involving more than one particle; and so have degree more than one. The color of an internal vertex will represent the type of interaction.
Thus, there is a set of field labels, one for each type of field; also a set of interaction labels, one for each permitted type of interaction. Depending on the type of field, field labels may or may not be orientable
. These labels are the colors of the graph.
Both edges and vertices are colored. Internal vertices are colored with the interaction label corresponding to the interaction they represent; similarly, edges are colored with field labels. The edges with orientable field labels (and only those) are directed; give the label the same direction as its edge. An external vertex is colored with the field label of its incident edge (and if the field label is orientable, with a head or a tail).
Each type of interaction must involve the right number of the right type of particles. To represent this, each interaction label has a matching condition: an of field labels. (The two directions of orientable labels are counted as distinct.)
An internal vertex, which is colored with an interaction label, satisfies the matching condition of its color if the vertex has degree equal to the size of the matching condition (as a set); and the incident edges can be ordered so that their labels are equal to the matching condition (as an ordered set). Loops are counted twice; once with each orientation.
A pseudograph is a Feynman graph if it is finite, partially directed, and colored, such that: Every edge is colored with a field label; an edge is directed if and only if its color is orientable. There are no isolated vertices; each vertex of degree 1 is colored with the field label (and orientation, if any) of its incident edge; every vertex of degree more than one is colored with an interaction label and satisfies the corresponding matching condition.
An automorphism
of a Feynman graph is a map from the graph onto itself which preserves the coloring and the graph structure (both the orientation of edges and their incidence with vertices) and leaves the external vertices untouched. The size of the automorphism group is called the symmetry factor. For the purposes of computing the symmetry factor, it has to be assumed that the head and the tail of even the unoriented edges are distinct.
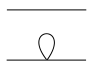 A Feynman graph decomposes uniquely into a union of connected components
A Feynman graph decomposes uniquely into a union of connected components
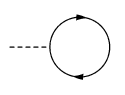
. A vacuum bubble is a connected component without any external vertices . (A Feynman graph without any vacuum bubbles is a bubbleless graph.) A tadpole
is a connected component with only one external vertex. The external vertices (each with its single incident edge) are legs.
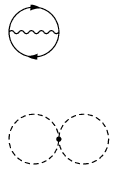
 The connected components of a Feynman graph are analysed as follows: Define a relation weakly connected between the vertices: two vertices are weakly connected if and only if no edge can be cut so as separate the vertices. (In graph theory
The connected components of a Feynman graph are analysed as follows: Define a relation weakly connected between the vertices: two vertices are weakly connected if and only if no edge can be cut so as separate the vertices. (In graph theory
, this is weakly 2-line-connected
.)
The following lemmata are then obvious, at least in the sense of Laplace:
A one particle irreducible (1PI) subgraph of a Feynman graph is the subgraph induced by an equivalence class which is not an external vertex.
The reduced graph of a Feynman graph is the graph produced by identifying all equivalent vertices (that is, each vertex with all other vertices weakly connected to it). The points of the reduced graph are the external vertices and the one particle irreducible subgraphs of the Feynman graph; its edges are the bridges.
Isolated vertices of the reduced graph are bubbles. Any other tree in the forest can be simplified by:
and repeating as often as possible. Neither kind of simplification can change the external vertices. Eventually a tree will be left with no vertices of either kind.
The resulting simplified tree is unique; it does not depend on the order of simplification. It will have the same number of legs as the corresponding component of the original Feynman graph. If this component had no legs, it was a bubble; the simplified tree will be a single vertex. If it had one leg, it was a tadpole; the simplified tree will have exactly one edge connecting two vertices (the graph K2). If it had at least two legs, every other vertex of the simplified tree will have degree at least three.
s), and one to each field label (called bare propagators). The initial conditions provide a position/momentum
for each external vertex. Contraction of these will result in a value for each graph; computation of this value often requires some regularization
.
Usually, in quantum field theory
and statistical mechanics
, each of the operators is just a multiplication by a complex
constant, so the value is their product, effectively also a complex number. In other applications, the value will be more general.
The correlation function is the sum over all bubbleless Feynman graphs (with the given external vertices and positions/momenta) of the values computed for each graph, each divided by its symmetry factor. There are almost always infinitely many such graphs and, usually, this sum does not converge, but instead gives an asymptotic series in the coupling constant
s.
Because every such graph can be reduced uniquely into a forest of reduced trees, we can use a two step procedure to compute the correlation function.
Because the sum is not convergent in general, much less absolutely convergent, there might be some problems with the rearrangement. In the usual derivations of the feynman rules using perturbation theory
, the infinite series is summed in the order of the power of the coupling constant
s (in other words, according to the number of vertices) while the 1PI method performs the summation in a different order. This has led to some occasional subtleties. See resummation
.
The previous algorithm used 1PIs as an intermediate step. This isn't the only possible algorithm. For instance, we might have used two particle irreducible subgraphs in an intermediate step instead.
Feynman diagram
Feynman diagrams are a pictorial representation scheme for the mathematical expressions governing the behavior of subatomic particles, first developed by the Nobel Prize-winning American physicist Richard Feynman, and first introduced in 1948...
in a particular application of quantum field theory
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
.
(The most common use is when each field has quanta
Quantum
In physics, a quantum is the minimum amount of any physical entity involved in an interaction. Behind this, one finds the fundamental notion that a physical property may be "quantized," referred to as "the hypothesis of quantization". This means that the magnitude can take on only certain discrete...
(particles) associated with it - since the quantum of the electromagnetic field
Electromagnetic field
An electromagnetic field is a physical field produced by moving electrically charged objects. It affects the behavior of charged objects in the vicinity of the field. The electromagnetic field extends indefinitely throughout space and describes the electromagnetic interaction...
is a photon
Photon
In physics, a photon is an elementary particle, the quantum of the electromagnetic interaction and the basic unit of light and all other forms of electromagnetic radiation. It is also the force carrier for the electromagnetic force...
. For simplicity, we will discuss them in terms of that case. Those who would apply Feynman diagram
Feynman diagram
Feynman diagrams are a pictorial representation scheme for the mathematical expressions governing the behavior of subatomic particles, first developed by the Nobel Prize-winning American physicist Richard Feynman, and first introduced in 1948...
s in other subjects or categories should translate the explanation with an appropriate isomorphism
Isomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
.)
A Feynman graph is a finite, partially directed
Directed graph
A directed graph or digraph is a pair G= of:* a set V, whose elements are called vertices or nodes,...
, colored pseudograph which satisfies certain conditions.("Pseudograph" means the graph
Graph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
can have loops
Loop (graph theory)
In graph theory, a loop is an edge that connects a vertex to itself. A simple graph contains no loops....
and multiple edges; "partially directed" means, in general, some edges are directed and others are not). Each edge represents a segment of the world line
World line
In physics, the world line of an object is the unique path of that object as it travels through 4-dimensional spacetime. The concept of "world line" is distinguished from the concept of "orbit" or "trajectory" by the time dimension, and typically encompasses a large area of spacetime wherein...
of a particle
Elementary particle
In particle physics, an elementary particle or fundamental particle is a particle not known to have substructure; that is, it is not known to be made up of smaller particles. If an elementary particle truly has no substructure, then it is one of the basic building blocks of the universe from which...
. There are two kinds of vertex: External vertices represent single particles entering or exiting the reaction as a whole, and so they have degree
Degree (graph theory)
In graph theory, the degree of a vertex of a graph is the number of edges incident to the vertex, with loops counted twice. The degree of a vertex v is denoted \deg. The maximum degree of a graph G, denoted by Δ, and the minimum degree of a graph, denoted by δ, are the maximum and minimum degree...
1. The color of an edge or an exterior vertex will represent the type of particle. Internal vertices represent interactions, involving more than one particle; and so have degree more than one. The color of an internal vertex will represent the type of interaction.
Thus, there is a set of field labels, one for each type of field; also a set of interaction labels, one for each permitted type of interaction. Depending on the type of field, field labels may or may not be orientable
Orientation
Orientation may refer to:* Orientation , a function of the mind* Orientation , a 1996 short film produced by the Church of Scientology...
. These labels are the colors of the graph.
Both edges and vertices are colored. Internal vertices are colored with the interaction label corresponding to the interaction they represent; similarly, edges are colored with field labels. The edges with orientable field labels (and only those) are directed; give the label the same direction as its edge. An external vertex is colored with the field label of its incident edge (and if the field label is orientable, with a head or a tail).
Each type of interaction must involve the right number of the right type of particles. To represent this, each interaction label has a matching condition: an of field labels. (The two directions of orientable labels are counted as distinct.)
An internal vertex, which is colored with an interaction label, satisfies the matching condition of its color if the vertex has degree equal to the size of the matching condition (as a set); and the incident edges can be ordered so that their labels are equal to the matching condition (as an ordered set). Loops are counted twice; once with each orientation.
A pseudograph is a Feynman graph if it is finite, partially directed, and colored, such that: Every edge is colored with a field label; an edge is directed if and only if its color is orientable. There are no isolated vertices; each vertex of degree 1 is colored with the field label (and orientation, if any) of its incident edge; every vertex of degree more than one is colored with an interaction label and satisfies the corresponding matching condition.
An automorphism
Automorphism
In mathematics, an automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, a symmetry of the object, and a way of mapping the object to itself while preserving all of its structure. The set of all automorphisms of an object forms a group, called the automorphism...
of a Feynman graph is a map from the graph onto itself which preserves the coloring and the graph structure (both the orientation of edges and their incidence with vertices) and leaves the external vertices untouched. The size of the automorphism group is called the symmetry factor. For the purposes of computing the symmetry factor, it has to be assumed that the head and the tail of even the unoriented edges are distinct.

Connected component (graph theory)
In graph theory, a connected component of an undirected graph is a subgraph in which any two vertices are connected to each other by paths, and which is connected to no additional vertices. For example, the graph shown in the illustration on the right has three connected components...
. A vacuum bubble is a connected component without any external vertices . (A Feynman graph without any vacuum bubbles is a bubbleless graph.) A tadpole
Tadpole (physics)
In quantum field theory, a tadpole is a one-loop Feynman diagram with one external leg, giving a contribution to a one-point correlation function . One-loop diagrams with a propagator that connects back to its originating vertex are often also referred as tadpoles...
is a connected component with only one external vertex. The external vertices (each with its single incident edge) are legs.


Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
, this is weakly 2-line-connected
Glossary of graph theory
Graph theory is a growing area in mathematical research, and has a large specialized vocabulary. Some authors use the same word with different meanings. Some authors use different words to mean the same thing. This page attempts to keep up with current usage....
.)
The following lemmata are then obvious, at least in the sense of Laplace:
- Weak connection is an equivalence relationEquivalence relationIn mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
.
- An edge connects different equivalence classes if and only if it is a bridgeBridge (graph theory)In graph theory, a bridge is an edge whose deletion increases the number of connected components. Equivalently, an edge is a bridge if and only if it is not contained in any cycle....
.
- There is at most one bridge connecting any two different equivalence classes.
- Each external vertex is the only element of its equivalence class.
A one particle irreducible (1PI) subgraph of a Feynman graph is the subgraph induced by an equivalence class which is not an external vertex.
- A Feynman graph is the edge-disjointGlossary of graph theoryGraph theory is a growing area in mathematical research, and has a large specialized vocabulary. Some authors use the same word with different meanings. Some authors use different words to mean the same thing. This page attempts to keep up with current usage....
union of its external vertices, one particle irreducible subgraphs, and bridges.
The reduced graph of a Feynman graph is the graph produced by identifying all equivalent vertices (that is, each vertex with all other vertices weakly connected to it). The points of the reduced graph are the external vertices and the one particle irreducible subgraphs of the Feynman graph; its edges are the bridges.
- The reduced graph of a Feynman graph is a forest. It is a treeTree (graph theory)In mathematics, more specifically graph theory, a tree is an undirected graph in which any two vertices are connected by exactly one simple path. In other words, any connected graph without cycles is a tree...
if and only if the Feynman graph is connected.
Isolated vertices of the reduced graph are bubbles. Any other tree in the forest can be simplified by:
- if any non-external vertex has degree 1 (and is not directly adjacent to an external vertex), removing it and its incident edge; or
- if any vertex has degree 2, replacing it and its incident edges by a single edge (which joins the vertices adjacent to the original vertex);
and repeating as often as possible. Neither kind of simplification can change the external vertices. Eventually a tree will be left with no vertices of either kind.
The resulting simplified tree is unique; it does not depend on the order of simplification. It will have the same number of legs as the corresponding component of the original Feynman graph. If this component had no legs, it was a bubble; the simplified tree will be a single vertex. If it had one leg, it was a tadpole; the simplified tree will have exactly one edge connecting two vertices (the graph K2). If it had at least two legs, every other vertex of the simplified tree will have degree at least three.
Numerical evaluation
The model will assign operators: one to each interaction label (called coupling constantCoupling constant
In physics, a coupling constant, usually denoted g, is a number that determines the strength of an interaction. Usually the Lagrangian or the Hamiltonian of a system can be separated into a kinetic part and an interaction part...
s), and one to each field label (called bare propagators). The initial conditions provide a position/momentum
Momentum
In classical mechanics, linear momentum or translational momentum is the product of the mass and velocity of an object...
for each external vertex. Contraction of these will result in a value for each graph; computation of this value often requires some regularization
Regularization (physics)
-Introduction:In physics, especially quantum field theory, regularization is a method of dealing with infinite, divergent, and non-sensical expressions by introducing an auxiliary concept of a regulator...
.
Usually, in quantum field theory
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
and statistical mechanics
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
, each of the operators is just a multiplication by a complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
constant, so the value is their product, effectively also a complex number. In other applications, the value will be more general.
The correlation function is the sum over all bubbleless Feynman graphs (with the given external vertices and positions/momenta) of the values computed for each graph, each divided by its symmetry factor. There are almost always infinitely many such graphs and, usually, this sum does not converge, but instead gives an asymptotic series in the coupling constant
Coupling constant
In physics, a coupling constant, usually denoted g, is a number that determines the strength of an interaction. Usually the Lagrangian or the Hamiltonian of a system can be separated into a kinetic part and an interaction part...
s.
Because every such graph can be reduced uniquely into a forest of reduced trees, we can use a two step procedure to compute the correlation function.
- 1. sum over 1PI graphs to get the one particle irreducible correlation functions.
- 2. compute the tadpole correlation functions and 2-point connected correlation functions.
- 3. using the intermediate values obtained from steps 1 and 2, sum over the reduced trees to get the n-point connected correlation functions
- 4. look at the forests and compute the correlation function from the connected correlation functions
Because the sum is not convergent in general, much less absolutely convergent, there might be some problems with the rearrangement. In the usual derivations of the feynman rules using perturbation theory
Perturbation theory
Perturbation theory comprises mathematical methods that are used to find an approximate solution to a problem which cannot be solved exactly, by starting from the exact solution of a related problem...
, the infinite series is summed in the order of the power of the coupling constant
Coupling constant
In physics, a coupling constant, usually denoted g, is a number that determines the strength of an interaction. Usually the Lagrangian or the Hamiltonian of a system can be separated into a kinetic part and an interaction part...
s (in other words, according to the number of vertices) while the 1PI method performs the summation in a different order. This has led to some occasional subtleties. See resummation
Resummation
In mathematics and theoretical physics, resummation is a procedure to obtain a finite result from a divergent sum of functions. Resummation involves a definition of another function in which the individual terms defining the original function are rescaled, and an integral transformation of this...
.
The previous algorithm used 1PIs as an intermediate step. This isn't the only possible algorithm. For instance, we might have used two particle irreducible subgraphs in an intermediate step instead.

