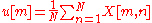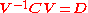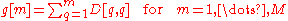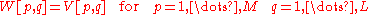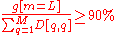
Principal components analysis - AbsoluteAstronomy.com

Principal component analysis (PCA) is a mathematical procedure that uses an orthogonal transformation to convert a set of observations of possibly correlated variables into a set of values of uncorrelated variables called principal components. The number of principal components is less than or equal to the number of original variables. This transformation is defined in such a way that the first principal component has as high a variance

Variance

In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...

as possible (that is, accounts for as much of the variability in the data as possible), and each succeeding component in turn has the highest variance possible under the constraint that it be orthogonal to (uncorrelated with) the preceding components. Principal components are guaranteed to be independent only if the data set is jointly normally distributed. PCA is sensitive to the relative scaling of the original variables. Depending on the field of application, it is also named the discrete Karhunen–Loève transform (KLT), the Hotelling
Harold Hotelling
Harold Hotelling was a mathematical statistician and an influential economic theorist.He was Associate Professor of Mathematics at Stanford University from 1927 until 1931, a member of the faculty of Columbia University from 1931 until 1946, and a Professor of Mathematical Statistics at the...

transform or proper orthogonal decomposition (POD).

PCA was invented in 1901 by Karl Pearson

Karl Pearson

Karl Pearson FRS was an influential English mathematician who has been credited for establishing the disciplineof mathematical statistics....

. Now it is mostly used as a tool in exploratory data analysis

Exploratory data analysis

In statistics, exploratory data analysis is an approach to analysing data sets to summarize their main characteristics in easy-to-understand form, often with visual graphs, without using a statistical model or having formulated a hypothesis...

and for making predictive models. PCA can be done by eigenvalue decomposition

Eigendecomposition of a matrix

In the mathematical discipline of linear algebra, eigendecomposition or sometimes spectral decomposition is the factorization of a matrix into a canonical form, whereby the matrix is represented in terms of its eigenvalues and eigenvectors...

of a data covariance matrix

Covariance matrix

In probability theory and statistics, a covariance matrix is a matrix whose element in the i, j position is the covariance between the i th and j th elements of a random vector...

or singular value decomposition

Singular value decomposition

In linear algebra, the singular value decomposition is a factorization of a real or complex matrix, with many useful applications in signal processing and statistics....

of a data matrix

Data matrix (multivariate statistics)

In multivariate statistics, a data matrix is a mathematical matrix of data whose rows represent different repetition of an experiment, and whose columns represent different types of datum . For example, suppose an experiment is run where 10 people are pulled off the street and asked four...

, usually after mean centering the data for each attribute. The results of a PCA are usually discussed in terms of component scores (the transformed variable values corresponding to a particular data point) and loadings (the weight by which each standardized original variable should be multiplied to get the component score).

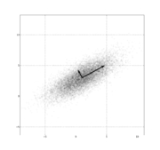
PCA is the simplest of the true eigenvector-based multivariate analyses. Often, its operation can be thought of as revealing the internal structure of the data in a way which best explains the variance in the data. If a multivariate dataset is visualised as a set of coordinates in a high-dimensional

Dimension (metadata)

In metadata, dimension is a set of equivalent units of measure, where equivalence between two units of measure is determined by the existence of a quantity preserving one-to-one correspondence between values measured in one unit of measure and values measured in the other unit of measure,...

data space (1 axis per variable), PCA can supply the user with a lower-dimensional picture, a "shadow" of this object when viewed from its (in some sense) most informative viewpoint. This is done by using only the first few principal components so that the dimensionality of the transformed data is reduced.

PCA is closely related to factor analysis

Factor analysis

Factor analysis is a statistical method used to describe variability among observed, correlated variables in terms of a potentially lower number of unobserved, uncorrelated variables called factors. In other words, it is possible, for example, that variations in three or four observed variables...

; indeed, some statistical packages deliberately conflate the two techniques. True factor analysis makes different assumptions about the underlying structure and solves eigenvectors of a slightly different matrix.

Details

PCA is mathematically defined as an orthogonal linear transformation

Linear transformation

In mathematics, a linear map, linear mapping, linear transformation, or linear operator is a function between two vector spaces that preserves the operations of vector addition and scalar multiplication. As a result, it always maps straight lines to straight lines or 0...

that transforms the data to a new coordinate system

Coordinate system

In geometry, a coordinate system is a system which uses one or more numbers, or coordinates, to uniquely determine the position of a point or other geometric element. The order of the coordinates is significant and they are sometimes identified by their position in an ordered tuple and sometimes by...

such that the greatest variance by any projection of the data comes to lie on the first coordinate (called the first principal component), the second greatest variance on the second coordinate, and so on.

Define a data matrix

Matrix (mathematics)

In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...

, X^T, with zero empirical mean (the empirical (sample) mean of the distribution has been subtracted from the data set), where each of the n rows represents a different repetition of the experiment, and each of the m columns gives a particular kind of datum (say, the results from a particular probe). (Note that what we are calling X^T is often alternatively denoted as X itself.) The singular value decomposition

Singular value decomposition

In linear algebra, the singular value decomposition is a factorization of a real or complex matrix, with many useful applications in signal processing and statistics....

of X is X = WΣV^T, where the m × m matrix W is the matrix of eigenvectors of XX^T, the matrix Σ is an m × n rectangular diagonal matrix with nonnegative real numbers on the diagonal, and the n × n matrix V is the matrix of eigenvectors of X^TX. The PCA transformation that preserves dimensionality (that is, gives the same number of principal components as original variables) is then given by:

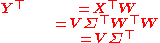
V is not uniquely defined in the usual case when m < n − 1, but Y will usually still be uniquely defined. Since W (by definition of the SVD of a real matrix) is an orthogonal matrix

Orthogonal matrix

In linear algebra, an orthogonal matrix , is a square matrix with real entries whose columns and rows are orthogonal unit vectors ....

, each row of Y^T is simply a rotation of the corresponding row of X^T. The first column of Y^T is made up of the "scores" of the cases with respect to the "principal" component, the next column has the scores with respect to the "second principal" component, and so on.

If we want a reduced-dimensionality representation, we can project X down into the reduced space defined by only the first L singular vectors, W_L:

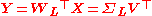where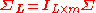

with

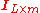the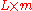

rectangular identity matrix.

The matrix W of singular vectors of X is equivalently the matrix W of eigenvectors of the matrix of observed covariances C = X X^T,

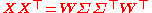
Given a set of points in Euclidean space

Euclidean space

In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...

, the first principal component corresponds to a line that passes through the multidimensional mean and minimizes the sum of squares of the distances of the points from the line. The second principal component corresponds to the same concept after all correlation with the first principal component has been subtracted from the points. The singular values (in Σ) are the square roots of the eigenvalues of the matrix XX^T. Each eigenvalue is proportional to the portion of the "variance" (more correctly of the sum of the squared distances of the points from their multidimensional mean) that is correlated with each eigenvector. The sum of all the eigenvalues is equal to the sum of the squared distances of the points from their multidimensional mean. PCA essentially rotates the set of points around their mean in order to align with the principal components. This moves as much of the variance as possible (using an orthogonal transformation) into the first few dimensions. The values in the remaining dimensions, therefore, tend to be small and may be dropped with minimal loss of information. PCA is often used in this manner for dimensionality reduction

Dimensionality reduction

In machine learning, dimension reduction is the process of reducing the number of random variables under consideration, and can be divided into feature selection and feature extraction.-Feature selection:...

. PCA has the distinction of being the optimal orthogonal transformation for keeping the subspace that has largest "variance" (as defined above). This advantage, however, comes at the price of greater computational requirements if compared, for example and when applicable, to the discrete cosine transform

Discrete cosine transform

A discrete cosine transform expresses a sequence of finitely many data points in terms of a sum of cosine functions oscillating at different frequencies. DCTs are important to numerous applications in science and engineering, from lossy compression of audio and images A discrete cosine transform...

. Nonlinear dimensionality reduction

Nonlinear dimensionality reduction

High-dimensional data, meaning data that requires more than two or three dimensions to represent, can be difficult to interpret. One approach to simplification is to assume that the data of interest lies on an embedded non-linear manifold within the higher-dimensional space...

techniques tend to be more computationally demanding than PCA.

PCA is sensitive to the scaling of the variables. If we have just two variables and they have the same sample variance and are positively correlated, then the PCA will entail a rotation by 45° and the "loadings" for the two variables with respect to the principal component will be equal. But if we multiply all values of the first variable by 100, then the principal component will be almost the same as that variable, with a small contribution from the other variable, whereas the second component will be almost aligned with the second original variable. This means that whenever the different variables have different units (like temperature and mass), PCA is a somewhat arbitrary method of analysis. (Different results would be obtained if one used Fahrenheit rather than Celsius for example.) Note that Pearson's original paper was entitled "On Lines and Planes of Closest Fit to Systems of Points in Space" – "in space" implies physical Euclidean space where such concerns do not arise. One way of making the PCA less arbitrary is to use variables scaled so as to have unit variance.

Discussion

Mean subtraction (a.k.a. "mean centering") is necessary for performing PCA to ensure that the first principal component describes the direction of maximum variance. If mean subtraction is not performed, the first principal component might instead correspond more or less to the mean of the data. A mean of zero is needed for finding a basis that minimizes the mean square error of the approximation of the data.

Assuming zero empirical mean (the empirical mean of the distribution has been subtracted from the data set), the principal component w₁ of a data set X can be defined as:

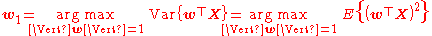
(See arg max for the notation.) With the first k − 1 components, the kth component can be found by subtracting the first

principal components from X:

and by substituting this as the new data set to find a principal component in

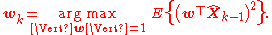
PCA is equivalent to empirical orthogonal functions

Empirical orthogonal functions

In statistics and signal processing, the method of empirical orthogonal function analysis is a decomposition of a signal or data set in terms of orthogonal basis functions which are determined from the data. It is the same as performing a principal components analysis on the data, except that the...

(EOF), a name which is used in meteorology

Meteorology

Meteorology is the interdisciplinary scientific study of the atmosphere. Studies in the field stretch back millennia, though significant progress in meteorology did not occur until the 18th century. The 19th century saw breakthroughs occur after observing networks developed across several countries...

.

An autoencoder

Autoencoder

An auto-encoder is an artificial neural network used for learning efficient codings.The aim of an auto-encoder is to learn a compressed representation for a set of data....

neural network

Artificial neural network

An artificial neural network , usually called neural network , is a mathematical model or computational model that is inspired by the structure and/or functional aspects of biological neural networks. A neural network consists of an interconnected group of artificial neurons, and it processes...

with a linear hidden layer is similar to PCA. Upon convergence, the weight vectors of the K neurons in the hidden layer will form a basis for the space spanned by the first K principal components. Unlike PCA, this technique will not necessarily produce orthogonal vectors.

PCA is a popular primary technique in pattern recognition

Pattern recognition

In machine learning, pattern recognition is the assignment of some sort of output value to a given input value , according to some specific algorithm. An example of pattern recognition is classification, which attempts to assign each input value to one of a given set of classes...

. It is not, however, optimized for class separability. An alternative is the linear discriminant analysis

Linear discriminant analysis

Linear discriminant analysis and the related Fisher's linear discriminant are methods used in statistics, pattern recognition and machine learning to find a linear combination of features which characterizes or separates two or more classes of objects or events...

, which does take this into account.

Table of symbols and abbreviations

Symbol	Meaning	Dimensions	Indices
	data matrix, consisting of the set of all data vectors, one vector per column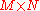
	the number of column vectors in the data set		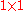scalar
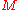	the number of elements in each column vector (dimension)		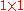scalar
	the number of dimensions in the dimensionally reduced subspace,	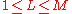	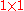scalar
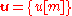	vector of empirical mean Mean In statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean.... s, one mean for each row m of the data matrix
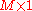	vector of empirical standard deviation Standard deviation Standard deviation is a widely used measure of variability or diversity used in statistics and probability theory. It shows how much variation or "dispersion" there is from the average... s, one standard deviation for each row m of the data matrix
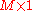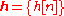	vector of all 1's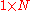
	deviation Deviation Deviation may refer to:* Deviation , the difference between the value of an observation and the mean of the population in mathematics and statistics** Standard deviation, which is based on the square of the difference... s from the mean of each row m of the data matrix
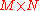	z-scores, computed using the mean and standard deviation for each row m of the data matrix
	covariance matrix Covariance matrix In probability theory and statistics, a covariance matrix is a matrix whose element in the i, j position is the covariance between the i th and j th elements of a random vector...
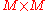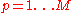	correlation matrix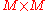
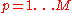	matrix consisting of the set of all eigenvectors of C, one eigenvector per column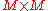
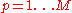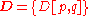	diagonal matrix Diagonal matrix In linear algebra, a diagonal matrix is a matrix in which the entries outside the main diagonal are all zero. The diagonal entries themselves may or may not be zero... consisting of the set of all eigenvalues of C along its principal diagonal, and 0 for all other elements
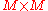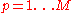	matrix of basis vectors, one vector per column, where each basis vector is one of the eigenvectors of C, and where the vectors in W are a sub-set of those in V
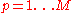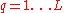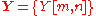	matrix consisting of N column vectors, where each vector is the projection of the corresponding data vector from matrix X onto the basis vectors contained in the columns of matrix W.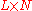

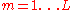Properties and limitations of PCA

As noted above, the results of PCA depend on the scaling of the variables.

The applicability of PCA is limited by certain assumptions made in its derivation.

Computing PCA using the covariance method

The following is a detailed description of PCA using the covariance method (see also here). But note that it is better to use the singular value decomposition (using standard software).

The goal is to transform a given data set X of dimension M to an alternative data set Y of smaller dimension L. Equivalently, we are seeking to find the matrix Y, where Y is the Karhunen–Loève transform (KLT) of matrix X:

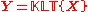
Organize the data set

Suppose you have data comprising a set of observations of M variables, and you want to reduce the data so that each observation can be described with only L variables, L < M. Suppose further, that the data are arranged as a set of N data vectors

with each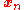

representing a single grouped observation of the M variables.

Write as column vectors, each of which has M rows.
Place the column vectors into a single matrix X of dimensions M × N.

Calculate the empirical mean

Find the empirical mean along each dimension m = 1, ..., M.
Place the calculated mean values into an empirical mean vector u of dimensions M × 1.

Calculate the deviations from the mean

Mean subtraction is an integral part of the solution towards finding a principal component basis that minimizes the mean square error of approximating the data. Hence we proceed by centering the data as follows:

Subtract the empirical mean vector u from each column of the data matrix X.
Store mean-subtracted data in the M × N matrix B.

where h is a 1 × N row vector of all 1s:

Find the covariance matrix

Find the M × M empirical covariance matrix
Covariance matrix
In probability theory and statistics, a covariance matrix is a matrix whose element in the i, j position is the covariance between the i th and j th elements of a random vector...

C from the outer product
Outer product
In linear algebra, the outer product typically refers to the tensor product of two vectors. The result of applying the outer product to a pair of vectors is a matrix...

of matrix B with itself:

where

is the expected value

Expected value

In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...

operator,

is the outer product operator, and

is the conjugate transpose

Conjugate transpose

In mathematics, the conjugate transpose, Hermitian transpose, Hermitian conjugate, or adjoint matrix of an m-by-n matrix A with complex entries is the n-by-m matrix A* obtained from A by taking the transpose and then taking the complex conjugate of each entry...

operator. Note that if B consists entirely of real numbers, which is the case in many applications, the "conjugate transpose" is the same as the regular transpose

Transpose

In linear algebra, the transpose of a matrix A is another matrix AT created by any one of the following equivalent actions:...

Please note that the information in this section is indeed a bit fuzzy. Outer products apply to vectors. For tensor cases we should apply tensor products, but the covariance matrix in PCA is a sum of outer products between its sample vectors; indeed, it could be represented as B.B*. See the covariance matrix sections on the discussion page for more information.

Find the eigenvectors and eigenvalues of the covariance matrix

Compute the matrix V of eigenvectors which diagonalizes
Diagonalizable matrix
In linear algebra, a square matrix A is called diagonalizable if it is similar to a diagonal matrix, i.e., if there exists an invertible matrix P such that P −1AP is a diagonal matrix...

the covariance matrix C:

where D is the diagonal matrix

Diagonal matrix

In linear algebra, a diagonal matrix is a matrix in which the entries outside the main diagonal are all zero. The diagonal entries themselves may or may not be zero...

of eigenvalues of C. This step will typically involve the use of a computer-based algorithm for computing eigenvectors and eigenvalues. These algorithms are readily available as sub-components of most matrix algebra

Matrix algebra

Matrix algebra may refer to:*Matrix theory, is the branch of mathematics that studies matrices*Matrix ring, thought of as an algebra over a field or a commutative ring...

systems, such as R (programming language)

R (programming language)

R is a programming language and software environment for statistical computing and graphics. The R language is widely used among statisticians for developing statistical software, and R is widely used for statistical software development and data analysis....

, MATLAB

MATLAB

MATLAB is a numerical computing environment and fourth-generation programming language. Developed by MathWorks, MATLAB allows matrix manipulations, plotting of functions and data, implementation of algorithms, creation of user interfaces, and interfacing with programs written in other languages,...

, Mathematica

Mathematica

Mathematica is a computational software program used in scientific, engineering, and mathematical fields and other areas of technical computing...

, SciPy

SciPy

SciPy is an open source library of algorithms and mathematical tools for the Python programming language.SciPy contains modules for optimization, linear algebra, integration, interpolation, special functions, FFT, signal and image processing, ODE solvers and other tasks common in science and...

, IDL

IDL

- General :* International Date Line, the time zone date boundary* Intermediate density lipoprotein* John F. Kennedy International Airport, from when it was named "Idlewild Airport" * International Drivers License...

(Interactive Data Language), or GNU Octave

GNU Octave

GNU Octave is a high-level language, primarily intended for numerical computations. It provides a convenient command-line interface for solving linear and nonlinear problems numerically, and for performing other numerical experiments using a language that is mostly compatible with MATLAB...

as well as OpenCV

OpenCV

OpenCV is a library of programming functions mainly aimed at real time computer vision, developed by Intel and now supported by Willow Garage. It is free for use under the open source BSD license. The library is cross-platform. It focuses mainly on real-time image processing...

Matrix D will take the form of an M × M diagonal matrix, where

is the mth eigenvalue of the covariance matrix C, and

Matrix V, also of dimension M × M, contains M column vectors, each of length M, which represent the M eigenvectors of the covariance matrix C.
The eigenvalues and eigenvectors are ordered and paired. The mth eigenvalue corresponds to the mth eigenvector.

Rearrange the eigenvectors and eigenvalues

Sort the columns of the eigenvector matrix V and eigenvalue matrix D in order of decreasing eigenvalue.
Make sure to maintain the correct pairings between the columns in each matrix.

Compute the cumulative energy content for each eigenvector

The eigenvalues represent the distribution of the source data's energy among each of the eigenvectors, where the eigenvectors form a basis
Basis (linear algebra)
In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...

for the data. The cumulative energy content g for the mth eigenvector is the sum of the energy content across all of the eigenvalues from 1 through m:

Select a subset of the eigenvectors as basis vectors

Save the first L columns of V as the M × L matrix W:

where

Use the vector g as a guide in choosing an appropriate value for L. The goal is to choose a value of L as small as possible while achieving a reasonably high value of g on a percentage basis. For example, you may want to choose L so that the cumulative energy g is above a certain threshold, like 90 percent. In this case, choose the smallest value of L such that

Convert the source data to z-scores

Create an M × 1 empirical standard deviation vector s from the square root of each element along the main diagonal of the covariance matrix C:

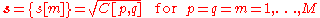
Calculate the M × N z-score
Standard score
In statistics, a standard score indicates how many standard deviations an observation or datum is above or below the mean. It is a dimensionless quantity derived by subtracting the population mean from an individual raw score and then dividing the difference by the population standard deviation...

matrix:

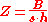(divide element-by-element)

Note: While this step is useful for various applications as it normalizes the data set with respect to its variance, it is not integral part of PCA/KLT

Project the z-scores of the data onto the new basis

The projected vectors are the columns of the matrix

W* is the conjugate transpose
Conjugate transpose
In mathematics, the conjugate transpose, Hermitian transpose, Hermitian conjugate, or adjoint matrix of an m-by-n matrix A with complex entries is the n-by-m matrix A* obtained from A by taking the transpose and then taking the complex conjugate of each entry...

of the eigenvector matrix.
The columns of matrix Y represent the Karhunen–Loeve transforms (KLT) of the data vectors in the columns of matrix X.

Derivation of PCA using the covariance method

Let X be a d-dimensional random vector expressed as column vector. Without loss of generality, assume X has zero mean.

We want to find

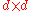orthonormal transformation matrix

Orthonormal basis

In mathematics, particularly linear algebra, an orthonormal basis for inner product space V with finite dimension is a basis for V whose vectors are orthonormal. For example, the standard basis for a Euclidean space Rn is an orthonormal basis, where the relevant inner product is the dot product of...

P so that PX has a diagonal covariant matrix (i.e. PX is a random vector with all its distinct components pairwise uncorrelated).

A quick computation assuming

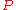were unitary yields: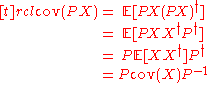

Hence

holds if and only if

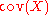were diagonalisable by

.

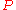This is very constructive, as cov(X) is guaranteed to be a non-negative definite matrix and thus is guaranteed to be diagonalisable by some unitary matrix.

Computing principal components iteratively

In practical implementations especially with high dimensional data (large m), the covariance method is rarely used because it is not efficient. One way to compute the first principal component efficiently is shown in the following pseudo-code, for a data matrix X^T with zero mean, without ever computing its covariance matrix. Note that here a zero mean data matrix means that the columns of X^T should each have zero mean.

a random vector
do c times:

(a vector of length m)
for each row

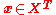
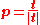
return

This algorithm is simply an efficient way of calculating XX^Tp, normalizing, and placing the result back in p (Power iteration

Power iteration

In mathematics, the power iteration is an eigenvalue algorithm: given a matrix A, the algorithm will produce a number λ and a nonzero vector v , such that Av = λv....

). It avoids the nm² operations of calculating the covariance matrix.
p will typically get close to the first principal component of X^T within a small number of iterations, c. (The magnitude of t will be larger after each iteration. Convergence can be detected when it increases by an amount too small for the precision of the machine.)

Subsequent principal components can be computed by subtracting component p from X^T (see Gram–Schmidt) and then repeating this algorithm to find the next principal component. However this simple approach is not numerically stable if more than a small number of principal components are required, because imprecisions in the calculations will additively affect the estimates of subsequent principal components. More advanced methods build on this basic idea, as with the closely related Lanczos algorithm

Lanczos algorithm

The Lanczos algorithm is an iterative algorithm invented by Cornelius Lanczos that is an adaptation of power methods to find eigenvalues and eigenvectors of a square matrix or the singular value decomposition of a rectangular matrix. It is particularly useful for finding decompositions of very...

.

One way to compute the eigenvalue that corresponds with each principal component is to measure the difference in sum-squared-distance between the rows and the mean, before and after subtracting out the principal component. The eigenvalue that corresponds with the component that was removed is equal to this difference.

The NIPALS method

For very high-dimensional datasets, such as those generated in the *omics sciences (e.g., genomics

Genomics

Genomics is a discipline in genetics concerning the study of the genomes of organisms. The field includes intensive efforts to determine the entire DNA sequence of organisms and fine-scale genetic mapping efforts. The field also includes studies of intragenomic phenomena such as heterosis,...

, metabolomics

Metabolomics

Metabolomics is the scientific study of chemical processes involving metabolites. Specifically, metabolomics is the "systematic study of the unique chemical fingerprints that specific cellular processes leave behind", the study of their small-molecule metabolite profiles...

) it is usually only necessary to compute the first few PCs. The non-linear iterative partial least squares

Non-linear iterative partial least squares

In statistics, non-linear iterative partial least squares is an algorithm for computing the first few components in a principal component or partial least squares analysis. For very high-dimensional datasets, such as those generated in the 'omics sciences it is usually only necessary to compute...

(NIPALS) algorithm calculates t₁ and p₁' from X. The outer product, t₁p₁' can then be subtracted from X leaving the residual matrix E₁. This can be then used to calculate subsequent PCs. This results in a dramatic reduction in computational time since calculation of the covariance matrix is avoided.

Relation between PCA and K-means clustering

It has been shown recently (2007)
that the relaxed solution of K-means clustering, specified by the cluster indicators, is given by the PCA principal components, and the PCA subspace spanned by the principal directions is identical to the cluster centroid subspace specified by the between-class scatter matrix

Scatter matrix

In multivariate statistics and probability theory, the scatter matrix is a statistic that is used to make estimates of the covariance matrix of the multivariate normal distribution.-Definition:...

. Thus PCA automatically projects to the subspace where the global solution of K-means clustering lies, and thus facilitates K-means clustering to find near-optimal solutions.

Correspondence analysis

Correspondence analysis
Correspondence analysis
Correspondence analysis is a multivariate statistical technique proposed by Hirschfeld and later developed by Jean-Paul Benzécri. It is conceptually similar to principal component analysis, but applies to categorical rather than continuous data...

(CA)
was developed by Jean-Paul Benzécri

Jean-Paul Benzécri

Jean-Paul Benzécri is a French statistician. He studied at École Normale Supérieure and has been professor at Université Pierre-et-Marie-Curie in Paris. He is most famous for the development of the Correspondence analysis, a statistical technique for analyzing contingency tables...

and is conceptually similar to PCA, but scales the data (which should be non-negative) so that rows and columns are treated equivalently. It is traditionally applied to contingency tables.
CA decomposes the chi-squared

Chi-squared

In statistics, the term chi-squared has different uses:*chi-squared distribution, a continuous probability distribution;*chi-squared statistic, a statistic used in some statistical tests;...

statistic associated to this table into orthogonal factors.
Because CA is a descriptive technique, it can be applied to tables for which the chi-squared statistic is appropriate or not.
Several variants of CA are available including detrended correspondence analysis

Detrended Correspondence Analysis

Detrended correspondence analysis is a multivariate statistical technique widely used by ecologists to find the main factors or gradients in large, species-rich but usually sparse data matrices that typify ecological community data. For example, Hill and Gauch analyse the data of a vegetation...

and canonical correspondence analysis. One special extension is multiple correspondence analysis

Multiple correspondence analysis

In statistics, multiple correspondence analysis is a data analysis technique for nominal categorical data, used to detect and represent underlying structures in a data set. It does this by representing data as points in a low-dimensional Euclidean space. The procedure thus appears to be the...

, which may be seen as the counterpart of principal component analysis for categorical data.

Nonlinear generalizations

Most of the modern methods for nonlinear dimensionality reduction

Nonlinear dimensionality reduction

find their theoretical and algorithmic roots in PCA or K-means. Pearson's original idea was to take a straight line (or plane) which will be "the best fit" to a set of data points. Principal curve
Curve
In mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...

s and manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....

s give the natural geometric framework for PCA generalization and extend the geometric interpretation of PCA by explicitly constructing an embedded manifold for data approximation

Approximation

An approximation is a representation of something that is not exact, but still close enough to be useful. Although approximation is most often applied to numbers, it is also frequently applied to such things as mathematical functions, shapes, and physical laws.Approximations may be used because...

, and by encoding using standard geometric projection

Projection (mathematics)

Generally speaking, in mathematics, a projection is a mapping of a set which is idempotent, which means that a projection is equal to its composition with itself. A projection may also refer to a mapping which has a left inverse. Bot notions are strongly related, as follows...

onto the manifold, as it is illustrated by Fig.
See also the elastic map

Elastic map

Elastic maps provide a tool for nonlinear dimensionality reduction. By their construction, they are system of elastic springs embedded in the dataspace. This system approximates a low-dimensional manifold...

algorithm and principal geodesic analysis

Principal geodesic analysis

In geometric data analysis and statistical shape analysis, principal geodesic analysis is a generalization of principal component analysis to a non-Euclidean, non-linear setting of manifolds suitable for use with shape descriptors such as medial representations....

Multilinear generalizations

In multilinear subspace learning

Multilinear subspace learning

Multilinear subspace learning aims to learn a specific small part of a large space of multidimensional objects having a particular desired property. It is a dimensionality reduction approach for finding a low-dimensional representation with certain preferred characteristics of high-dimensional...

, PCA is generalized to multilinear PCA

Multilinear principal component analysis

Multilinear principal-component analysis is a mathematical procedure that uses multiple orthogonal transformations to convert a set of multidimensional objects into another set of multidimensional objects of lower dimensions. There is one orthogonal transformation for each dimension...

(MPCA) that extracts features directly from tensor representations. MPCA is solved by performing PCA in each mode of the tensor iteratively. MPCA has been applied to face recognition, gait recognition, etc. MPCA is further extended to uncorrelated MPCA, non-negative MPCA and robust MPCA.

Higher order

N-way principal component analysis may be performed with models such as Tucker decomposition

Tucker decomposition

In mathematics, Tucker decomposition decomposes a tensor into a set of matrices and one small core tensor. It is named after Ledyard R. Tuckeralthough it goes back to Hitchcock in 1927....

, PARAFAC, multiple factor analysis, co-inertia analysis, STATIS, and DISTATIS.

Robustness - Weighted PCA

While PCA finds the mathematically optimal method (as in minimizing the squared error), it is sensitive to outlier

Outlier

In statistics, an outlier is an observation that is numerically distant from the rest of the data. Grubbs defined an outlier as: An outlying observation, or outlier, is one that appears to deviate markedly from other members of the sample in which it occurs....

s in the data that produce large errors PCA tries to avoid. It therefore is common practice to remove outliers before computing PCA. However, in some contexts, outliers can be difficult to identify. For example in data mining

Data mining

Data mining , a relatively young and interdisciplinary field of computer science is the process of discovering new patterns from large data sets involving methods at the intersection of artificial intelligence, machine learning, statistics and database systems...

algorithms like correlation clustering

Correlation clustering

In machine learning, correlation clustering or cluster editing operates in a scenario where the relationship between the objects are known instead of the actual representation of the objects...

, the assignment of points to clusters and outliers is not known beforehand. A recently proposed generalization of PCA based on a Weighted PCA increases robustness by assigning different weights to data objects based on their estimated relevancy.

Software/source code

Cornell Spectrum Imager - An open-source toolset built on ImageJ. Enables quick easy PCA analysis for 3D datacubes.
imDEV Free Excel addin to calculate principal components using R package pcaMethods.
"ViSta: The Visual Statistics System" a free software that provides principal components analysis, simple and multiple correspondence analysis.
"Spectramap" is software to create a biplot
Biplot
Biplots are a type of exploratory graph used in statistics, a generalization of the simple two-variable scatterplot. A biplot allows information on both samples and variables of a data matrix to be displayed graphically. Samples are displayed as points while variables are displayed either as...

using principal components analysis, correspondence analysis or spectral map analysis.
XLSTAT
XLSTAT
XLSTAT is a commercial statistical and multivariate analysis software. The software has been developed by Addinsoft and was introduced by Thierry Fahmy, the founder of Addinsoft, in 1993. It is a Microsoft Excel add-in...

is a statistical and multivariate analysis software including Principal Component Analysis among other multivariate tools.
FinMath, a .NET
.NET Framework
The .NET Framework is a software framework that runs primarily on Microsoft Windows. It includes a large library and supports several programming languages which allows language interoperability...

numerical library containing an implementation of PCA.
The Unscrambler
The Unscrambler
The Unscrambler is a commercial software product for multivariate data analysis, used primarily for calibration in the application of near infrared spectroscopy and development of predictive models for use in real-time spectroscopic analysis of materials. The software was originally developed in...

is a multivariate analysis software enabling Principal Component Analysis (PCA) with PCA Projection.
Computer Vision Library
In the MATLAB
MATLAB
MATLAB is a numerical computing environment and fourth-generation programming language. Developed by MathWorks, MATLAB allows matrix manipulations, plotting of functions and data, implementation of algorithms, creation of user interfaces, and interfacing with programs written in other languages,...

Statistics Toolbox, the functions princomp and wmspca give the principal components, while the function pcares gives the residuals and reconstructed matrix for a low-rank PCA approximation. Here is a link to a MATLAB implementation of PCA PcaPress .
NMath
NMath
NMath is a numerical package for the Microsoft .NET Framework. It is developed by CenterSpace Software. Version 1.0 was released in March, 2003 as NMath Core...

, a numerical library containing PCA for the .NET Framework
.NET Framework
The .NET Framework is a software framework that runs primarily on Microsoft Windows. It includes a large library and supports several programming languages which allows language interoperability...

.
in Octave
GNU Octave
GNU Octave is a high-level language, primarily intended for numerical computations. It provides a convenient command-line interface for solving linear and nonlinear problems numerically, and for performing other numerical experiments using a language that is mostly compatible with MATLAB...

, a free software computational environment mostly compatible with MATLAB, the function princomp gives the principal component.
in the free
Free software
Free software, software libre or libre software is software that can be used, studied, and modified without restriction, and which can be copied and redistributed in modified or unmodified form either without restriction, or with restrictions that only ensure that further recipients can also do...

statistical package R
R (programming language)
R is a programming language and software environment for statistical computing and graphics. The R language is widely used among statisticians for developing statistical software, and R is widely used for statistical software development and data analysis....

, the functions princomp and prcomp can be used for principal component analysis; prcomp uses singular value decomposition
Singular value decomposition
In linear algebra, the singular value decomposition is a factorization of a real or complex matrix, with many useful applications in signal processing and statistics....

which generally gives better numerical accuracy. Recently there has been an explosion in implementations of principal component analysis in various R packages, generally in packages for specific purposes. For a more complete list, see here: http://cran.r-project.org/web/views/Multivariate.html.
In XLMiner, the Principal Components tab can be used for principal component analysis.
In IDL, the principal components can be calculated using the function pcomp.
Weka
Weka (machine learning)
Weka is a popular suite of machine learning software written in Java, developed at the University of Waikato, New Zealand...

computes principal components (javadoc).
Software for analyzing multivariate data with instant response using PCA
Orange (software)
Orange (software)
Orange is a component-based data mining and machine learning software suite, featuring friendly yet powerful and flexible visual programming front-end for explorative data analysis and visualization, and Python bindings and libraries for scripting...

supports PCA through its Linear Projection widget.
A version of PCA adapted for population genetics analysis can be found in the suite EIGENSOFT.
PCA can also be performed by the statistical software Partek Genomics Suite, developed by Partek.

The source of this article is wikipedia, the free encyclopedia. The text of this article is licensed under the GFDL.