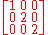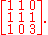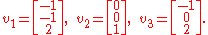Diagonalizable matrix
Encyclopedia
In linear algebra
, a square matrix A is called diagonalizable if it is similar to a diagonal matrix
, i.e., if there exists an invertible matrix P such that P −1AP is a diagonal matrix. If V is a finite-dimensional vector space
, then a linear map T : V → V is called diagonalizable if there exists a basis
of V with respect to which T is represented by a diagonal matrix. Diagonalization is the process of finding a corresponding diagonal matrix for a diagonalizable matrix or linear map. A square matrix which is not diagonalizable is called defective
.
Diagonalizable matrices and maps are of interest because diagonal matrices are especially easy to handle: their eigenvalues and eigenvectors are known and one can raise a diagonal matrix to a power by simply raising the diagonal entries to that same power. Geometrically, a diagonalizable matrix is an inhomogeneous dilation (or anisotropic scaling) – it scales
the space, as does a homogeneous dilation, but by a different factor in each direction, determined by the scale factors on each axis (diagonal entries).
Another characterization: A matrix or linear map is diagonalizable over the field F if and only if its minimal polynomial
is a product of distinct linear factors over F. (Put in another way, a matrix is diagonalisable if and only if all of its elementary divisors are linear.)
The following sufficient (but not necessary) condition is often useful.
Let A be a matrix over F. If A is diagonalizable, then so is any power of it. Conversely, if A is invertible, F is algebraically closed, and An is diagonalizable for some n that is not an integer multiple of the characteristic of F, then A is diagonalizable. Proof: If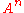 is diagonalizable, then A is annihilated by some polynomial
is diagonalizable, then A is annihilated by some polynomial  , which has no multiple root (since
, which has no multiple root (since 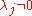 ) and is divided by the minimal polynomial of A.
) and is divided by the minimal polynomial of A.
As a rule of thumb, over C almost every matrix is diagonalizable. More precisely: the set of complex n-by-n matrices that are not diagonalizable over C, considered as a subset
of Cn×n, has Lebesgue measure
zero. One can also say that the diagonalizable matrices form a dense subset with respect to the Zariski topology
: the complement lies inside the set where the discriminant
of the characteristic polynomial vanishes, which is a hypersurface
. From that follows also density in the usual (strong) topology given by a norm
. The same is not true over R.
The Jordan–Chevalley decomposition expresses an operator as the sum of its semisimple (i.e., diagonalizable) part and its nilpotent
part. Hence, a matrix is diagonalizable if and only if its nilpotent part is zero. Put in another way, a matrix is diagonalizable if each block in its Jordan form has no nilpotent part; i.e., one-by-one matrix.

then:
Writing P as a block matrix
of its column vectors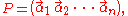
the above equation can be rewritten as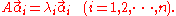
So the column vectors of P are eigenvectors of A, and the corresponding diagonal entry is the corresponding eigenvalue. The invertibility of P also suggests that the eigenvectors are linearly independent and form the basis of Fn. This is the necessary and sufficient condition for diagonalizability and the canonical approach of diagonalization.
When the matrix A is a Hermitian matrix (resp. symmetric matrix), eigenvectors of A can be chosen to form an orthonormal basis
of Cn (resp. Rn). Under such circumstance P will be a unitary matrix (resp. orthogonal matrix
) and P-1 equals the conjugate transpose
(resp. transpose
) of P.
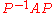 is a diagonal matrix for every A in the set. The following theorem characterises simultaneously diagonalisable matrices: A set of diagonalizable matrices commutes if and only if the set is simultaneously diagonalisable.
is a diagonal matrix for every A in the set. The following theorem characterises simultaneously diagonalisable matrices: A set of diagonalizable matrices commutes if and only if the set is simultaneously diagonalisable.
The set of all n-by-n diagonalisable matrices (over C) with n > 1 is not simultaneously diagonalisable. For instance, the matrices
are diagonalizable but not simultaneously diagonalizable because they do not commute.
A set consists of commuting normal matrices
if and only if it is simultaneously diagonalisable by a unitary matrix; that is, there exists a unitary matrix U such that is diagonal for every A in the set.
is diagonal for every A in the set.
In the language of Lie theory
, a set of simultaneously diagonalisable matrices generate a toral Lie algebra
.
. This happens more generally if the algebraic and geometric multiplicities of an eigenvalue do not coincide. For instance, consider
This matrix is not diagonalizable: there is no matrix U such that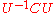 is a diagonal matrix. Indeed, C has one eigenvalue (namely zero) and this eigenvalue has algebraic multiplicity 2 and geometric multiplicity 1.
is a diagonal matrix. Indeed, C has one eigenvalue (namely zero) and this eigenvalue has algebraic multiplicity 2 and geometric multiplicity 1.
Some real matrices are not diagonalizable over the reals. Consider for instance the matrix
The matrix B does not have any real eigenvalues, so there is no real matrix Q such that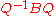 is a diagonal matrix. However, we can diagonalize B if we allow complex numbers. Indeed, if we take
is a diagonal matrix. However, we can diagonalize B if we allow complex numbers. Indeed, if we take
then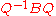 is diagonal.
is diagonal.
Note that the above examples show that the sum of diagonalizable matrices need not be diagonalizable.
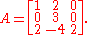
This matrix has eigenvalues
So A is a 3-by-3 matrix with 3 different eigenvalues, therefore it is diagonalizable. Note that if there are exactly n distinct eigenvalues in an n×n matrix then this matrix is diagonalizable.
These eigenvalues are the values that will appear in the diagonalized form of matrix , so by finding the eigenvalues of
, so by finding the eigenvalues of  we have diagonalized it. We could stop here, but it is a good check to use the eigenvectors to diagonalize
we have diagonalized it. We could stop here, but it is a good check to use the eigenvectors to diagonalize  .
.
The eigenvectors of A are
One can easily check that
Now, let P be the matrix with these eigenvectors as its columns:
Note there is no preferred order of the eigenvectors in P; changing the order of the eigenvectors in P just changes the order of the eigenvalues in the diagonalized form of A.
Then P diagonalizes A, as a simple computation confirms: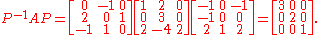
Note that the eigenvalues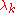 appear in the diagonal matrix.
appear in the diagonal matrix.
 , where
, where  ,
,
and the Diagonalization matrix is:
is: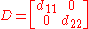
Distribute into the column vectors of
into the column vectors of  .
.
Then can be broken down to its column vectors as follows:
can be broken down to its column vectors as follows: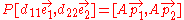
Multiplying on the left side of the equation gives:
on the left side of the equation gives:
Setting each entry of the matrix to its corresponding entry: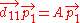

Then the equations can be solved as follows, using the same process for both: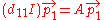
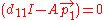
and it solves for , which is the first entry in the diagonal matrix, and also the first eigen value.
, which is the first entry in the diagonal matrix, and also the first eigen value.
to compute the powers of a matrix A efficiently, provided the matrix is diagonalizable. Suppose we have found that
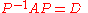
is a diagonal matrix. Then, as the matrix product is associative,

and the latter is easy to calculate since it only involves the powers of a diagonal matrix. This approach can be generalized to matrix exponential
and other matrix function
s since they can be defined as power series.
This is particularly useful in finding closed form expressions for terms of linear recursive sequences, such as the Fibonacci number
s.
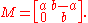
Calculating the various powers of M reveals a surprising pattern: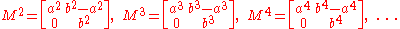
The above phenomenon can be explained by diagonalizing M. To accomplish this, we need a basis of R2 consisting of eigenvectors
of M. One such eigenvector basis is given by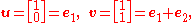
where ei denotes the standard basis of Rn.
The reverse change of basis is given by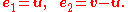
Straightforward calculations show that
Thus, a and b are the eigenvalues corresponding to u and v, respectively.
By linearity of matrix multiplication, we have that
Switching back to the standard basis, we have

The preceding relations, expressed in matrix form, are
thereby explaining the above phenomenon.
and quantum chemical
computations matrix diagonalization is one of the most frequently applied numerical processes. The basic reason is that the time-independent Schrödinger equation
is an eigenvalue equation, albeit in most of the physical situations on an infinite dimensional space (a Hilbert space
). A very common approximation is to truncate Hilbert space to finite dimension, after which the Schrödinger equation can be formulated as an eigenvalue problem of a real symmetric, or complex Hermitian, matrix. Formally this approximation is founded on the variational principle
, valid for Hamiltonians that are bounded from below.
But also first-order perturbation theory for degenerate states leads to a matrix eigenvalue problem.
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, a square matrix A is called diagonalizable if it is similar to a diagonal matrix
Diagonal matrix
In linear algebra, a diagonal matrix is a matrix in which the entries outside the main diagonal are all zero. The diagonal entries themselves may or may not be zero...
, i.e., if there exists an invertible matrix P such that P −1AP is a diagonal matrix. If V is a finite-dimensional vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
, then a linear map T : V → V is called diagonalizable if there exists a basis
Basis (linear algebra)
In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
of V with respect to which T is represented by a diagonal matrix. Diagonalization is the process of finding a corresponding diagonal matrix for a diagonalizable matrix or linear map. A square matrix which is not diagonalizable is called defective
Defective matrix
In linear algebra, a defective matrix is a square matrix that does not have a complete basis of eigenvectors, and is therefore not diagonalizable. In particular, an n × n matrix is defective if and only if it does not have n linearly independent eigenvectors...
.
Diagonalizable matrices and maps are of interest because diagonal matrices are especially easy to handle: their eigenvalues and eigenvectors are known and one can raise a diagonal matrix to a power by simply raising the diagonal entries to that same power. Geometrically, a diagonalizable matrix is an inhomogeneous dilation (or anisotropic scaling) – it scales
Scaling (geometry)
In Euclidean geometry, uniform scaling is a linear transformation that enlarges or shrinks objects by a scale factor that is the same in all directions. The result of uniform scaling is similar to the original...
the space, as does a homogeneous dilation, but by a different factor in each direction, determined by the scale factors on each axis (diagonal entries).
Characterisation
The fundamental fact about diagonalizable maps and matrices is expressed by the following:- An n-by-n matrix A over the fieldField (mathematics)In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
F is diagonalizable if and only ifIf and only ifIn logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
the sum of the dimensions of its eigenspaces is equal to n, which is the case if and only if there exists a basisBasis (linear algebra)In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
of Fn consisting of eigenvectors of A. If such a basis has been found, one can form the matrix P having these basis vectors as columns, and P−1AP will be a diagonal matrix. The diagonal entries of this matrix are the eigenvalues of A. - A linear map T: V → V is diagonalizable if and only if the sum of the dimensions of its eigenspaces is equal to dim(V), which is the case if and only if there exists a basis of V consisting of eigenvectors of T. With respect to such a basis, T will be represented by a diagonal matrix. The diagonal entries of this matrix are the eigenvalues of T.
Another characterization: A matrix or linear map is diagonalizable over the field F if and only if its minimal polynomial
Minimal polynomial (linear algebra)
In linear algebra, the minimal polynomial of an n-by-n matrix A over a field F is the monic polynomial P over F of least degree such that P=0...
is a product of distinct linear factors over F. (Put in another way, a matrix is diagonalisable if and only if all of its elementary divisors are linear.)
The following sufficient (but not necessary) condition is often useful.
- An n-by-n matrix A is diagonalizable over the field F if it has n distinct eigenvalues in F, i.e. if its characteristic polynomialCharacteristic polynomialIn linear algebra, one associates a polynomial to every square matrix: its characteristic polynomial. This polynomial encodes several important properties of the matrix, most notably its eigenvalues, its determinant and its trace....
has n distinct roots in F. Opposite may be false, let us consider
-
-
- which has eigenvalues 1, 2, 2 (not all distinct) and is diagonalisable with diagonal form
-
- and similarity matrix
-
- A linear map T: V → V with n = dim(V) is diagonalizable if it has n distinct eigenvalues, i.e. if its characteristic polynomial has n distinct roots in F.
Let A be a matrix over F. If A is diagonalizable, then so is any power of it. Conversely, if A is invertible, F is algebraically closed, and An is diagonalizable for some n that is not an integer multiple of the characteristic of F, then A is diagonalizable. Proof: If
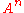 is diagonalizable, then A is annihilated by some polynomial
is diagonalizable, then A is annihilated by some polynomial  , which has no multiple root (since
, which has no multiple root (since 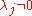 ) and is divided by the minimal polynomial of A.
) and is divided by the minimal polynomial of A.As a rule of thumb, over C almost every matrix is diagonalizable. More precisely: the set of complex n-by-n matrices that are not diagonalizable over C, considered as a subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
of Cn×n, has Lebesgue measure
Lebesgue measure
In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
zero. One can also say that the diagonalizable matrices form a dense subset with respect to the Zariski topology
Zariski topology
In algebraic geometry, the Zariski topology is a particular topology chosen for algebraic varieties that reflects the algebraic nature of their definition. It is due to Oscar Zariski and took a place of particular importance in the field around 1950...
: the complement lies inside the set where the discriminant
Discriminant
In algebra, the discriminant of a polynomial is an expression which gives information about the nature of the polynomial's roots. For example, the discriminant of the quadratic polynomialax^2+bx+c\,is\Delta = \,b^2-4ac....
of the characteristic polynomial vanishes, which is a hypersurface
Hypersurface
In geometry, a hypersurface is a generalization of the concept of hyperplane. Suppose an enveloping manifold M has n dimensions; then any submanifold of M of n − 1 dimensions is a hypersurface...
. From that follows also density in the usual (strong) topology given by a norm
Norm (mathematics)
In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
. The same is not true over R.
The Jordan–Chevalley decomposition expresses an operator as the sum of its semisimple (i.e., diagonalizable) part and its nilpotent
Nilpotent
In mathematics, an element x of a ring R is called nilpotent if there exists some positive integer n such that xn = 0....
part. Hence, a matrix is diagonalizable if and only if its nilpotent part is zero. Put in another way, a matrix is diagonalizable if each block in its Jordan form has no nilpotent part; i.e., one-by-one matrix.
Diagonalization
If a matrix A can be diagonalized, that is,
then:

Writing P as a block matrix
Block matrix
In the mathematical discipline of matrix theory, a block matrix or a partitioned matrix is a matrix broken into sections called blocks. Looking at it another way, the matrix is written in terms of smaller matrices. We group the rows and columns into adjacent 'bunches'. A partition is the rectangle...
of its column vectors
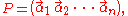
the above equation can be rewritten as
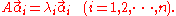
So the column vectors of P are eigenvectors of A, and the corresponding diagonal entry is the corresponding eigenvalue. The invertibility of P also suggests that the eigenvectors are linearly independent and form the basis of Fn. This is the necessary and sufficient condition for diagonalizability and the canonical approach of diagonalization.
When the matrix A is a Hermitian matrix (resp. symmetric matrix), eigenvectors of A can be chosen to form an orthonormal basis
Orthonormal basis
In mathematics, particularly linear algebra, an orthonormal basis for inner product space V with finite dimension is a basis for V whose vectors are orthonormal. For example, the standard basis for a Euclidean space Rn is an orthonormal basis, where the relevant inner product is the dot product of...
of Cn (resp. Rn). Under such circumstance P will be a unitary matrix (resp. orthogonal matrix
Orthogonal matrix
In linear algebra, an orthogonal matrix , is a square matrix with real entries whose columns and rows are orthogonal unit vectors ....
) and P-1 equals the conjugate transpose
Conjugate transpose
In mathematics, the conjugate transpose, Hermitian transpose, Hermitian conjugate, or adjoint matrix of an m-by-n matrix A with complex entries is the n-by-m matrix A* obtained from A by taking the transpose and then taking the complex conjugate of each entry...
(resp. transpose
Transpose
In linear algebra, the transpose of a matrix A is another matrix AT created by any one of the following equivalent actions:...
) of P.
Simultaneous diagonalization
A set of matrices are said to be simultaneously diagonalisable if there exists a single invertible matrix P such that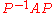 is a diagonal matrix for every A in the set. The following theorem characterises simultaneously diagonalisable matrices: A set of diagonalizable matrices commutes if and only if the set is simultaneously diagonalisable.
is a diagonal matrix for every A in the set. The following theorem characterises simultaneously diagonalisable matrices: A set of diagonalizable matrices commutes if and only if the set is simultaneously diagonalisable.The set of all n-by-n diagonalisable matrices (over C) with n > 1 is not simultaneously diagonalisable. For instance, the matrices

are diagonalizable but not simultaneously diagonalizable because they do not commute.
A set consists of commuting normal matrices
Normal matrix
A complex square matrix A is a normal matrix ifA^*A=AA^* \ where A* is the conjugate transpose of A. That is, a matrix is normal if it commutes with its conjugate transpose.If A is a real matrix, then A*=AT...
if and only if it is simultaneously diagonalisable by a unitary matrix; that is, there exists a unitary matrix U such that
 is diagonal for every A in the set.
is diagonal for every A in the set.In the language of Lie theory
Lie theory
Lie theory is an area of mathematics, developed initially by Sophus Lie.Early expressions of Lie theory are found in books composed by Lie with Friedrich Engel and Georg Scheffers from 1888 to 1896....
, a set of simultaneously diagonalisable matrices generate a toral Lie algebra
Toral Lie algebra
In mathematics, a toral Lie algebra is a Lie subalgebra of a general linear Lie algebra all of whose elements are diagonalizable . Equivalently, a Lie algebra is toral if it contains no nonzero nilpotent elements...
.
Diagonalizable matrices
- Involutions are diagonalisable over the reals (and indeed any field of characteristic not 2), with 1's and -1's on the diagonal
- Finite order endomorphismEndomorphismIn mathematics, an endomorphism is a morphism from a mathematical object to itself. For example, an endomorphism of a vector space V is a linear map ƒ: V → V, and an endomorphism of a group G is a group homomorphism ƒ: G → G. In general, we can talk about...
s are diagonalisable over the complex numbers (or any algebraically closed field where the characteristic of the field does not divide the order of the endomorphism) with roots of unity on the diagonal. This follows since the minimal polynomial is separableSeparable polynomialIn mathematics, two slightly different notions of separable polynomial are used, by different authors.According to the most common one, a polynomial P over a given field K is separable if all its roots are distinct in an algebraic closure of K, that is the number of its distinct roots is equal to...
, because the roots of unity are distinct. - Projections are diagonalizable, with 0's and 1's on the diagonal.
- Real symmetric matrices are diagonalizable by orthogonal matricesOrthogonal matrixIn linear algebra, an orthogonal matrix , is a square matrix with real entries whose columns and rows are orthogonal unit vectors ....
; i.e., given a real symmetric matrix ,
, 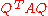 is diagonal for some orthogonal matrix
is diagonal for some orthogonal matrix  . More generally, matrices are diagonalizable by unitary matrices if and only if they are normalNormal matrixA complex square matrix A is a normal matrix ifA^*A=AA^* \ where A* is the conjugate transpose of A. That is, a matrix is normal if it commutes with its conjugate transpose.If A is a real matrix, then A*=AT...
. More generally, matrices are diagonalizable by unitary matrices if and only if they are normalNormal matrixA complex square matrix A is a normal matrix ifA^*A=AA^* \ where A* is the conjugate transpose of A. That is, a matrix is normal if it commutes with its conjugate transpose.If A is a real matrix, then A*=AT...
. In the case of the real symmetric matrix, we see that , so clearly
, so clearly  holds. Examples of normal matrices are real symmetric (or skew-symmetric) matrices (e.g. covariance matrices) and Hermitian matrices (or skew-Hermitian matrices). See spectral theoremSpectral theoremIn mathematics, particularly linear algebra and functional analysis, the spectral theorem is any of a number of results about linear operators or about matrices. In broad terms the spectral theorem provides conditions under which an operator or a matrix can be diagonalized...
holds. Examples of normal matrices are real symmetric (or skew-symmetric) matrices (e.g. covariance matrices) and Hermitian matrices (or skew-Hermitian matrices). See spectral theoremSpectral theoremIn mathematics, particularly linear algebra and functional analysis, the spectral theorem is any of a number of results about linear operators or about matrices. In broad terms the spectral theorem provides conditions under which an operator or a matrix can be diagonalized...
s for generalizations to infinite-dimensional vector spaces.
Matrices that are not diagonalizable
Some matrices are not diagonalizable over any field, most notably nonzero nilpotent matricesNilpotent matrix
In linear algebra, a nilpotent matrix is a square matrix N such thatN^k = 0\,for some positive integer k. The smallest such k is sometimes called the degree of N....
. This happens more generally if the algebraic and geometric multiplicities of an eigenvalue do not coincide. For instance, consider

This matrix is not diagonalizable: there is no matrix U such that
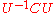 is a diagonal matrix. Indeed, C has one eigenvalue (namely zero) and this eigenvalue has algebraic multiplicity 2 and geometric multiplicity 1.
is a diagonal matrix. Indeed, C has one eigenvalue (namely zero) and this eigenvalue has algebraic multiplicity 2 and geometric multiplicity 1.Some real matrices are not diagonalizable over the reals. Consider for instance the matrix

The matrix B does not have any real eigenvalues, so there is no real matrix Q such that
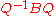 is a diagonal matrix. However, we can diagonalize B if we allow complex numbers. Indeed, if we take
is a diagonal matrix. However, we can diagonalize B if we allow complex numbers. Indeed, if we take
then
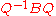 is diagonal.
is diagonal.Note that the above examples show that the sum of diagonalizable matrices need not be diagonalizable.
How to diagonalize a matrix
Consider a matrix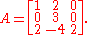
This matrix has eigenvalues
So A is a 3-by-3 matrix with 3 different eigenvalues, therefore it is diagonalizable. Note that if there are exactly n distinct eigenvalues in an n×n matrix then this matrix is diagonalizable.
These eigenvalues are the values that will appear in the diagonalized form of matrix
 , so by finding the eigenvalues of
, so by finding the eigenvalues of  we have diagonalized it. We could stop here, but it is a good check to use the eigenvectors to diagonalize
we have diagonalized it. We could stop here, but it is a good check to use the eigenvectors to diagonalize  .
.The eigenvectors of A are
One can easily check that

Now, let P be the matrix with these eigenvectors as its columns:

Note there is no preferred order of the eigenvectors in P; changing the order of the eigenvectors in P just changes the order of the eigenvalues in the diagonalized form of A.
Then P diagonalizes A, as a simple computation confirms:
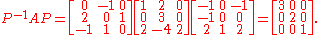
Note that the eigenvalues
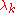 appear in the diagonal matrix.
appear in the diagonal matrix.Alternative Method
Starting with: , where
, where  ,
,and the Diagonalization matrix
 is:
is: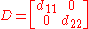
Distribute
 into the column vectors of
into the column vectors of  .
.
Then
 can be broken down to its column vectors as follows:
can be broken down to its column vectors as follows: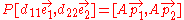
Multiplying
 on the left side of the equation gives:
on the left side of the equation gives:
Setting each entry of the matrix to its corresponding entry:
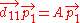

Then the equations can be solved as follows, using the same process for both:
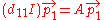
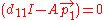
and it solves for
 , which is the first entry in the diagonal matrix, and also the first eigen value.
, which is the first entry in the diagonal matrix, and also the first eigen value.An application
Diagonalization can be usedto compute the powers of a matrix A efficiently, provided the matrix is diagonalizable. Suppose we have found that
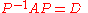
is a diagonal matrix. Then, as the matrix product is associative,

and the latter is easy to calculate since it only involves the powers of a diagonal matrix. This approach can be generalized to matrix exponential
Matrix exponential
In mathematics, the matrix exponential is a matrix function on square matrices analogous to the ordinary exponential function. Abstractly, the matrix exponential gives the connection between a matrix Lie algebra and the corresponding Lie group....
and other matrix function
Matrix function
In mathematics, a matrix function is a function which maps a matrix to another matrix.- Extending scalar functions to matrix functions :There are several techniques for lifting a real function to a square matrix function such that interesting properties are maintained...
s since they can be defined as power series.
This is particularly useful in finding closed form expressions for terms of linear recursive sequences, such as the Fibonacci number
Fibonacci number
In mathematics, the Fibonacci numbers are the numbers in the following integer sequence:0,\;1,\;1,\;2,\;3,\;5,\;8,\;13,\;21,\;34,\;55,\;89,\;144,\; \ldots\; ....
s.
Particular application
For example, consider the following matrix: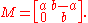
Calculating the various powers of M reveals a surprising pattern:
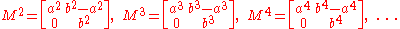
The above phenomenon can be explained by diagonalizing M. To accomplish this, we need a basis of R2 consisting of eigenvectors
of M. One such eigenvector basis is given by
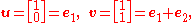
where ei denotes the standard basis of Rn.
The reverse change of basis is given by
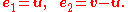
Straightforward calculations show that

Thus, a and b are the eigenvalues corresponding to u and v, respectively.
By linearity of matrix multiplication, we have that

Switching back to the standard basis, we have


The preceding relations, expressed in matrix form, are

thereby explaining the above phenomenon.
Quantum mechanical application
In quantum mechanicalQuantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
and quantum chemical
Quantum chemistry
Quantum chemistry is a branch of chemistry whose primary focus is the application of quantum mechanics in physical models and experiments of chemical systems...
computations matrix diagonalization is one of the most frequently applied numerical processes. The basic reason is that the time-independent Schrödinger equation
Schrödinger equation
The Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
is an eigenvalue equation, albeit in most of the physical situations on an infinite dimensional space (a Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
). A very common approximation is to truncate Hilbert space to finite dimension, after which the Schrödinger equation can be formulated as an eigenvalue problem of a real symmetric, or complex Hermitian, matrix. Formally this approximation is founded on the variational principle
Variational principle
A variational principle is a scientific principle used within the calculus of variations, which develops general methods for finding functions which minimize or maximize the value of quantities that depend upon those functions...
, valid for Hamiltonians that are bounded from below.
But also first-order perturbation theory for degenerate states leads to a matrix eigenvalue problem.
See also
- Defective matrixDefective matrixIn linear algebra, a defective matrix is a square matrix that does not have a complete basis of eigenvectors, and is therefore not diagonalizable. In particular, an n × n matrix is defective if and only if it does not have n linearly independent eigenvectors...
- Scaling (geometry)Scaling (geometry)In Euclidean geometry, uniform scaling is a linear transformation that enlarges or shrinks objects by a scale factor that is the same in all directions. The result of uniform scaling is similar to the original...
- Triangular matrixTriangular matrixIn the mathematical discipline of linear algebra, a triangular matrix is a special kind of square matrix where either all the entries below or all the entries above the main diagonal are zero...
- Semisimple operator
- Diagonalizable groupDiagonalizable groupIn mathematics, an affine group is said to be diagonalizable if it is isomorphic to a subgroup of Dn, the group of diagonal matrices. A diagonalizable group defined over k is said to split over k or k-split if the isomorphism is defined over k. This coincides with the usual notion of split for an...
- Jordan normal formJordan normal formIn linear algebra, a Jordan normal form of a linear operator on a finite-dimensional vector space is an upper triangular matrix of a particular form called Jordan matrix, representing the operator on some basis...
- Weight module – associative algebra generalization