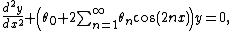Bloch wave - AbsoluteAstronomy.com

A Bloch wave or Bloch state, named after Felix Bloch

Felix Bloch

Felix Bloch was a Swiss physicist, working mainly in the U.S.-Life and work:Bloch was born in Zürich, Switzerland to Jewish parents Gustav and Agnes Bloch. He was educated there and at the Eidgenössische Technische Hochschule, also in Zürich. Initially studying engineering he soon changed to physics...

, is the wavefunction

Wavefunction

Not to be confused with the related concept of the Wave equationA wave function or wavefunction is a probability amplitude in quantum mechanics describing the quantum state of a particle and how it behaves. Typically, its values are complex numbers and, for a single particle, it is a function of...

of a particle (usually, an electron

Electron

The electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...

) placed in a periodic potential

Particle in a one-dimensional lattice (periodic potential)

In quantum mechanics, the particle in a one-dimensional lattice is a problem that occurs in the model of a periodic crystal lattice. The potential is caused by ions in the periodic structure of the crystal creating an electromagnetic field so electrons are subject to a regular potential inside...

. Bloch's theorem states that the energy eigenfunction for such a system may be written as the product of a plane wave

Plane wave

In the physics of wave propagation, a plane wave is a constant-frequency wave whose wavefronts are infinite parallel planes of constant peak-to-peak amplitude normal to the phase velocity vector....

envelope function and a periodic function

Periodic function

In mathematics, a periodic function is a function that repeats its values in regular intervals or periods. The most important examples are the trigonometric functions, which repeat over intervals of length 2π radians. Periodic functions are used throughout science to describe oscillations,...

(periodic Bloch function)

that has the same periodicity as the potential:

The corresponding energy eigenvalues are ϵ_n(k) = ϵ_n(k + K), periodic with periodicity K of a reciprocal lattice

Reciprocal lattice

In physics, the reciprocal lattice of a lattice is the lattice in which the Fourier transform of the spatial function of the original lattice is represented. This space is also known as momentum space or less commonly k-space, due to the relationship between the Pontryagin duals momentum and...

vector. The energies associated with the index n vary continuously with wave vector

Wave vector

In physics, a wave vector is a vector which helps describe a wave. Like any vector, it has a magnitude and direction, both of which are important: Its magnitude is either the wavenumber or angular wavenumber of the wave , and its direction is ordinarily the direction of wave propagation In...

k and form an energy band identified by band index n. The eigenvalues for given n are periodic in k; all distinct values of ϵ_n(k) occur for k-values within the first Brillouin zone

Brillouin zone

In mathematics and solid state physics, the first Brillouin zone is a uniquely defined primitive cell in reciprocal space. The boundaries of this cell are given by planes related to points on the reciprocal lattice. It is found by the same method as for the Wigner–Seitz cell in the Bravais lattice...

of the reciprocal lattice.
In fact, the Bloch theorem is a direct consequence of the translational symmetry of crystals, which means that the crystal is invariant under a translational movement

of the form

, where

are integers and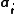

are the primitive lattice vectors. If

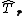denotes the translation operation that can be applied to a wave function in a direction of the form

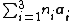, where

are integers, it can readily be seen that the operation forms a group with the same combination law as

. Since the crystalline system and hence its Hamiltonian is invariant after such translations, the translation operator must be commutative with the Hamiltonian operator, thus they can be simultaneously diagonalized. In this way, each eigenfunction of the Hamiltonian can be an eigenfunction of the translation operator. To maintain the wavefunction properly normalized, the eigenvalue for the translation operator must be of the form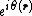

, where

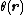is a function of the translation vector

. By applying two such translations

and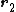

consecutively to one wavefunction, it can be shown that

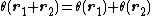. Thus the

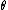function can be written as the dot product of the translation vectors

and a vector

because of the linearity of

. In this way, it has been deduced that an eigenfunction of the Hamiltonian operator of a system with discrete translational symmetry such as a crystal is always an eigenfunction of the discrete symmetrical translation operators

with eigenvalue

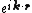. In other words, each eigenvalue of the Hamiltonian forms a basis for a one-dimensional representation of the group of translation operations specified by the Bravais lattice and the vector

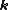can be considered to be a label for the irreducible representation

Group representation

In the mathematical field of representation theory, group representations describe abstract groups in terms of linear transformations of vector spaces; in particular, they can be used to represent group elements as matrices so that the group operation can be represented by matrix multiplication...

.
More generally, a Bloch-wave description applies to any wave-like phenomenon in a periodic medium. For example, a periodic dielectric

Dielectric

A dielectric is an electrical insulator that can be polarized by an applied electric field. When a dielectric is placed in an electric field, electric charges do not flow through the material, as in a conductor, but only slightly shift from their average equilibrium positions causing dielectric...

in electromagnetism

Electromagnetism

Electromagnetism is one of the four fundamental interactions in nature. The other three are the strong interaction, the weak interaction and gravitation...

leads to photonic crystal

Photonic crystal

Photonic crystals are periodic optical nanostructures that are designed to affect the motion of photons in a similar way that periodicity of a semiconductor crystal affects the motion of electrons...

s, and a periodic acoustic medium leads to phononic crystals. It is generally treated in the various forms of the dynamical theory of diffraction

Dynamical theory of diffraction

The dynamical theory of diffraction describes the interaction of waves with a regular lattice. The wave fields traditionally described are X-rays, neutrons or electrons and the regular lattice, atomic crystal structures or nanometer scaled multi-layers or self arranged systems...

.

The plane wave vector (Bloch wave vector) k, which when multiplied by the reduced Plank's constant is the particle's crystal momentum, is unique only up to a reciprocal lattice

Reciprocal lattice

vector, so one only needs to consider the wave vectors inside the first Brillouin zone. For a given wave vector and potential, there are a number of solutions, indexed by n, to Schrodinger's equation for a Bloch electron. These solutions, called bands, are separated in energy by a finite spacing at each k; if there is a separation that extends over all wave vectors, it is called a (complete) band gap

Band gap

In solid state physics, a band gap, also called an energy gap or bandgap, is an energy range in a solid where no electron states can exist. In graphs of the electronic band structure of solids, the band gap generally refers to the energy difference between the top of the valence band and the...

. The band structure

Electronic band structure

In solid-state physics, the electronic band structure of a solid describes those ranges of energy an electron is "forbidden" or "allowed" to have. Band structure derives from the diffraction of the quantum mechanical electron waves in a periodic crystal lattice with a specific crystal system and...

is the collection of energy eigenstates within the first Brillouin zone. All the properties of electrons in a periodic potential can be calculated from this band structure and the associated wave functions, at least within the independent electron approximation

Independent electron approximation

The independent electron approximation is used in both the free electron model and the nearly-free electron model. In this approximation we do not consider electron-electron interaction in a crystal...

.

A corollary of this result is that the Bloch wave vector k is a conserved quantity in a crystalline system (modulo addition of reciprocal lattice vectors), and hence the group velocity

Group velocity

The group velocity of a wave is the velocity with which the overall shape of the wave's amplitudes — known as the modulation or envelope of the wave — propagates through space....

of the wave is conserved. This means that electrons can propagate without scattering through a crystalline material, almost like free particles, and that electrical resistance

Electrical resistance

The electrical resistance of an electrical element is the opposition to the passage of an electric current through that element; the inverse quantity is electrical conductance, the ease at which an electric current passes. Electrical resistance shares some conceptual parallels with the mechanical...

in a crystalline conductor

Electrical conductor

In physics and electrical engineering, a conductor is a material which contains movable electric charges. In metallic conductors such as copper or aluminum, the movable charged particles are electrons...

only results from imperfections and finite size which break the periodicity and induce interaction with phonon

Phonon

In physics, a phonon is a collective excitation in a periodic, elastic arrangement of atoms or molecules in condensed matter, such as solids and some liquids...

s.

The concept of the Bloch state was developed by Felix Bloch

Felix Bloch

in 1928, to describe the conduction of electrons in crystalline solids. The same underlying mathematics, however, was also discovered independently several times: by George William Hill

George William Hill

George William Hill , was an American astronomer and mathematician.Hill was born in New York City, New York to painter and engraver John William Hill. and Catherine Smith Hill. He moved to West Nyack with his family when he was eight years old. After attending high school, Hill graduated from...

(1877), Gaston Floquet

Gaston Floquet

Achille Marie Gaston Floquet was a French mathematician, best known for his work in mathematical analysis, especially in theory of differential equations.-External links:...

(1883), and Alexander Lyapunov (1892). As a result, a variety of nomenclatures are common: applied to ordinary differential equations, it is called Floquet theory (or occasionally the Lyapunov–Floquet theorem). Various one-dimensional periodic potential equations have special names, for example, Hill's equation:

where the

are constants. Hill's equation is very general, as the θ-related terms may be viewed as a Fourier series

Fourier series

In mathematics, a Fourier series decomposes periodic functions or periodic signals into the sum of a set of simple oscillating functions, namely sines and cosines...

expansion of a periodic potential. Other much studied periodic one-dimensional equations are the Kronig–Penney model and Mathieu's equation

Mathieu function

In mathematics, the Mathieu functions are certain special functions useful for treating a variety of problems in applied mathematics, including*vibrating elliptical drumheads,*quadrupoles mass filters and quadrupole ion traps for mass spectrometry...

.

Graphical representation of Bloch Function

See also

Further reading