Linearized gravity
Encyclopedia
Linearized gravity is an approximation scheme in general relativity
in which the nonlinear contributions from the spacetime
metric
are ignored, simplifying the study of many problems while still producing useful approximate results.
,
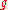, of spacetime is treated as a sum of an exact solution of Einstein's equations (often in Minkowski spacetime) and a perturbation
.
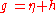
where η is the nondynamical background metric that is being perturbed about, and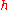
represents the deviation of the true metric (g) from flat spacetime.
The perturbation is treated using the methods of perturbation theory
, "linearized" by ignoring all terms of order higher than one (quadratic
in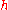
, cubic
in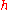
etc...) in the perturbation.
The method is used to derive the Newtonian limit, including the first corrections, much like for a derivation of the existence of gravitational wave
s that led, after quantization
, to graviton
s. This is why the conceptual approach of linearized gravity is the canonical one in particle physics
, string theory
, and more generally quantum field theory
where classical (bosonic) fields are expressed as coherent state
s of particles.
This approximation is also known as the weak-field approximation as it is only valid for h very small.
s with small "displacements" (diffeomorphisms with large displacements obviously violate the weak field approximation), which has the exact form (for infinitesimal transformations)
Where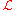
is the Lie derivative
and we used the fact that η does not transform (by definition). Note that we are raising and lowering the indices with respect to η and not g and taking the covariant derivative
s (Levi-Civita connection
) with respect to η. This is the standard practice in linearized gravity. The way of thinking in linearized gravity is this: the background metric η IS the metric and h is a field propagating over the spacetime with this metric.
In the weak field limit, this gauge transformation simplifies to
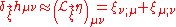
The weak-field approximation is useful in finding the values of certain constants, for example in the Einstein field equations
and in the Schwarzschild metric
.
and is used to simplify many problems in general relativity
and to discuss the phenomena of gravitational radiation. The approximation can also be used to derive Newtonian gravity as the weak-field approximation of Einsteinian gravity
.
The equations are obtained by assuming the spacetime metric
is only slightly different from some baseline metric (usually a Minkowski metric). Then the difference in the metrics can be considered as a field on the baseline metric, whose behaviour is approximated by a set of linear equations.
in the form
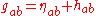
where
is the Minkowski metric and 
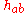— sometimes written as 
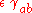— is the deviation of 
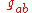from it. 
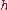must be negligible compared to 
: 
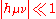(and similarly for all derivatives of 
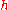). Then one ignores all products of 
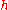(or its derivatives) with 
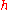or its derivatives (equivalent to ignoring all terms of higher order than 1 in 
). It is further assumed in this approximation scheme that all indices of h and its derivatives are raised and lowered with 
.
The metric h is clearly symmetric, since g and η are. The consistency condition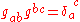
shows that
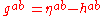
The Christoffel symbols
can be calculated as
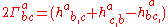
where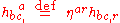
, and this is used to calculate the Riemann tensor:
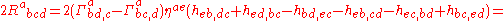
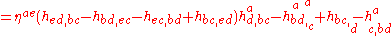
Using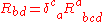
gives
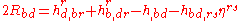
For Ricci scalar we have:
Then the linearized Einstein equations are
or
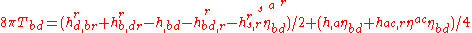
Or, equivalently:
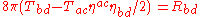
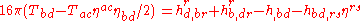
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
in which the nonlinear contributions from the spacetime
Spacetime
In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
metric
Metric tensor (general relativity)
In general relativity, the metric tensor is the fundamental object of study. It may loosely be thought of as a generalization of the gravitational field familiar from Newtonian gravitation...
are ignored, simplifying the study of many problems while still producing useful approximate results.
The method
In linearized gravity the metric tensorMetric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
,
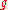, of spacetime is treated as a sum of an exact solution of Einstein's equations (often in Minkowski spacetime) and a perturbationPerturbation theory
Perturbation theory comprises mathematical methods that are used to find an approximate solution to a problem which cannot be solved exactly, by starting from the exact solution of a related problem...
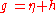
.where η is the nondynamical background metric that is being perturbed about, and
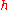represents the deviation of the true metric (g) from flat spacetime.The perturbation is treated using the methods of perturbation theory
Perturbation theory
Perturbation theory comprises mathematical methods that are used to find an approximate solution to a problem which cannot be solved exactly, by starting from the exact solution of a related problem...
, "linearized" by ignoring all terms of order higher than one (quadratic
Quadratic
In mathematics, the term quadratic describes something that pertains to squares, to the operation of squaring, to terms of the second degree, or equations or formulas that involve such terms...
in
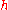, cubicCubic function
In mathematics, a cubic function is a function of the formf=ax^3+bx^2+cx+d,\,where a is nonzero; or in other words, a polynomial of degree three. The derivative of a cubic function is a quadratic function...
in
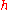etc...) in the perturbation.Applications
The Einstein field equations, being nonlinear in the metric, are difficult to solve exactly and the above perturbation scheme allows linearised Einstein field equations to be obtained. These equations are linear in the metric, and the sum of two solutions of the linearized EFE is also a solution. The idea of 'ignoring the nonlinear part' is thus encapsulated in this linearization procedure.The method is used to derive the Newtonian limit, including the first corrections, much like for a derivation of the existence of gravitational wave
Gravitational wave
In physics, gravitational waves are theoretical ripples in the curvature of spacetime which propagates as a wave, traveling outward from the source. Predicted to exist by Albert Einstein in 1916 on the basis of his theory of general relativity, gravitational waves theoretically transport energy as...
s that led, after quantization
Quantization (physics)
In physics, quantization is the process of explaining a classical understanding of physical phenomena in terms of a newer understanding known as "quantum mechanics". It is a procedure for constructing a quantum field theory starting from a classical field theory. This is a generalization of the...
, to graviton
Graviton
In physics, the graviton is a hypothetical elementary particle that mediates the force of gravitation in the framework of quantum field theory. If it exists, the graviton must be massless and must have a spin of 2...
s. This is why the conceptual approach of linearized gravity is the canonical one in particle physics
Particle physics
Particle physics is a branch of physics that studies the existence and interactions of particles that are the constituents of what is usually referred to as matter or radiation. In current understanding, particles are excitations of quantum fields and interact following their dynamics...
, string theory
String theory
String theory is an active research framework in particle physics that attempts to reconcile quantum mechanics and general relativity. It is a contender for a theory of everything , a manner of describing the known fundamental forces and matter in a mathematically complete system...
, and more generally quantum field theory
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
where classical (bosonic) fields are expressed as coherent state
Coherent state
In quantum mechanics a coherent state is a specific kind of quantum state of the quantum harmonic oscillator whose dynamics most closely resembles the oscillating behaviour of a classical harmonic oscillator...
s of particles.
This approximation is also known as the weak-field approximation as it is only valid for h very small.
Weak-field approximation
In a weak-field approximation, the gauge symmetry is associated with diffeomorphismDiffeomorphism
In mathematics, a diffeomorphism is an isomorphism in the category of smooth manifolds. It is an invertible function that maps one differentiable manifold to another, such that both the function and its inverse are smooth.- Definition :...
s with small "displacements" (diffeomorphisms with large displacements obviously violate the weak field approximation), which has the exact form (for infinitesimal transformations)
Where
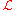is the Lie derivativeLie derivative
In mathematics, the Lie derivative , named after Sophus Lie by Władysław Ślebodziński, evaluates the change of a vector field or more generally a tensor field, along the flow of another vector field...
and we used the fact that η does not transform (by definition). Note that we are raising and lowering the indices with respect to η and not g and taking the covariant derivative
Covariant derivative
In mathematics, the covariant derivative is a way of specifying a derivative along tangent vectors of a manifold. Alternatively, the covariant derivative is a way of introducing and working with a connection on a manifold by means of a differential operator, to be contrasted with the approach given...
s (Levi-Civita connection
Levi-Civita connection
In Riemannian geometry, the Levi-Civita connection is a specific connection on the tangent bundle of a manifold. More specifically, it is the torsion-free metric connection, i.e., the torsion-free connection on the tangent bundle preserving a given Riemannian metric.The fundamental theorem of...
) with respect to η. This is the standard practice in linearized gravity. The way of thinking in linearized gravity is this: the background metric η IS the metric and h is a field propagating over the spacetime with this metric.
In the weak field limit, this gauge transformation simplifies to
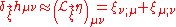
The weak-field approximation is useful in finding the values of certain constants, for example in the Einstein field equations
Einstein field equations
The Einstein field equations or Einstein's equations are a set of ten equations in Albert Einstein's general theory of relativity which describe the fundamental interaction of gravitation as a result of spacetime being curved by matter and energy...
and in the Schwarzschild metric
Schwarzschild metric
In Einstein's theory of general relativity, the Schwarzschild solution describes the gravitational field outside a spherical, uncharged, non-rotating mass such as a star, planet, or black hole. It is also a good approximation to the gravitational field of a slowly rotating body like the Earth or...
.
Linearised Einstein field equations
The linearised Einstein field equations (linearised EFE) are an approximation to Einstein's field equations that is valid for a weak gravitational fieldGravitational field
The gravitational field is a model used in physics to explain the existence of gravity. In its original concept, gravity was a force between point masses...
and is used to simplify many problems in general relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
and to discuss the phenomena of gravitational radiation. The approximation can also be used to derive Newtonian gravity as the weak-field approximation of Einsteinian gravity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
.
The equations are obtained by assuming the spacetime metric
Metric tensor (general relativity)
In general relativity, the metric tensor is the fundamental object of study. It may loosely be thought of as a generalization of the gravitational field familiar from Newtonian gravitation...
is only slightly different from some baseline metric (usually a Minkowski metric). Then the difference in the metrics can be considered as a field on the baseline metric, whose behaviour is approximated by a set of linear equations.
Derivation for the Minkowski metric
Starting with the metric for a spacetimeSpacetime
In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
in the form
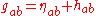
where
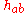is the Minkowski metric and — sometimes written as 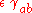— is the deviation of 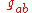from it. 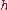must be negligible compared to : 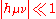(and similarly for all derivatives of 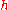). Then one ignores all products of 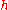(or its derivatives) with 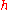or its derivatives (equivalent to ignoring all terms of higher order than 1 in ). It is further assumed in this approximation scheme that all indices of h and its derivatives are raised and lowered with .The metric h is clearly symmetric, since g and η are. The consistency condition
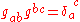shows that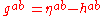The Christoffel symbols
Christoffel symbols
In mathematics and physics, the Christoffel symbols, named for Elwin Bruno Christoffel , are numerical arrays of real numbers that describe, in coordinates, the effects of parallel transport in curved surfaces and, more generally, manifolds. As such, they are coordinate-space expressions for the...
can be calculated as
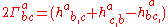
where
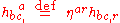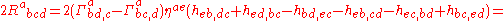
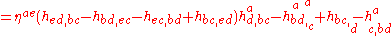
, and this is used to calculate the Riemann tensor:Using
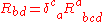gives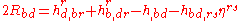For Ricci scalar we have:
Then the linearized Einstein equations are
or
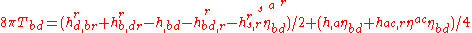
Or, equivalently:
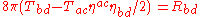
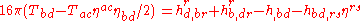
Applications
The linearised EFE are used primarily in the theory of gravitational radiation, where the gravitational field far from the source is approximated by these equations.See also
- Correspondence principleCorrespondence principleIn physics, the correspondence principle states that the behavior of systems described by the theory of quantum mechanics reproduces classical physics in the limit of large quantum numbers....
- GravitomagnetismGravitomagnetismGravitomagnetism , refers to a set of formal analogies between Maxwell's field equations and an approximation, valid under certain conditions, to the Einstein field equations for general relativity. The most common version of GEM is valid only far from isolated sources, and for slowly moving test...
- Parameterized post-Newtonian formalismParameterized post-Newtonian formalismPost-Newtonian formalism is a calculational tool that expresses Einstein's equations of gravity in terms of the lowest-order deviations from Newton's theory. This allows approximations to Einstein's equations to be made in the case of weak fields...
- Quasinormal modeQuasinormal mode-Wave Mechanics:Quasinormal modes are the modes of energy dissipation of aperturbed object or field. A familiar example is theperturbation of a wine glass with a knife: the glass begins to...