
Parameterized post-Newtonian formalism
Encyclopedia
Post-Newtonian formalism is a calculational tool that expresses Einstein's (nonlinear) equations of gravity in terms of the lowest-order deviations from Newton's theory. This allows approximations to Einstein's equations to be made in the case of weak fields. Higher order terms can be added to increase accuracy, but for strong fields sometimes it is preferable to solve the complete equations numerically. Some of these post-Newtonian approximations are expansions in a small parameter, which is the ratio of the velocity of the matter forming the gravitational field to the speed of light, which in this case is better called the speed of gravity. In the limit, when the fundamental speed of gravity becomes infinite, the post-Newtonian expansion reduces to Newton's law of gravity.
The parameterized post-Newtonian formalism or PPN formalism is a version of this formulation that explicitly details the parameters in which a general theory of gravity can differ from Newtonian gravity. It is used as a tool to compare Newtonian and Einsteinian gravity in the limit in which the gravitational field
is weak and generated by objects moving slowly compared to the speed of light
. In general, PPN formalism can be applied to all metric theories of gravitation in which all bodies satisfy the Einstein equivalence principle (EEP). The speed of light remains constant in PPN formalism and it assumes that the metric tensor
is always symmetric.
in 1922. However, they dealt solely with the vacuum gravitational field outside an isolated spherical body. Dr. Ken Nordtvedt
(1968, 1969) expanded this to include 7 parameters. Clifford Martin Will
(1971) introduced a stressed, continuous matter description of celestial bodies.
The versions described here are based on Wei-Tou Ni
(1972), Will and Nordtvedt (1972), Charles W. Misner
et al. (1973) (see Gravitation (book)
), and Will (1981, 1993) and have 10 parameters.
. In the notation of Will (1971), Ni (1972) and Misner et al. (1973) they have the following values:
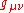 is the 4 by 4 symmetric metric tensor and indexes
is the 4 by 4 symmetric metric tensor and indexes  and
and  go from 1 to 3.
go from 1 to 3.
In Einstein's theory, the values of these parameters are chosen (1) to fit Newton's Law of gravity in the limit of velocities and mass approaching zero, (2) to ensure conservation of energy, mass, momentum, and angular momentum, and (3) to make the equations independent of the reference frame. In this notation, general relativity has PPN parameters
 and
and 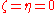






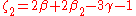


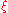 is calculated from
is calculated from 
The meaning of these is that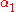 ,
,  and
and 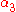 measure the extent of preferred frame effects.
measure the extent of preferred frame effects.  ,
,  ,
, 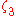 ,
,  and
and  measure the failure of conservation of energy, momentum and angular momentum.
measure the failure of conservation of energy, momentum and angular momentum.
In this notation, general relativity has PPN parameters and
and 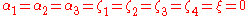
The mathematical relationship between the metric, metric potentials and PPN parameters for this notation is:
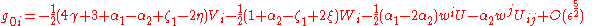

where repeated indexes are summed. is on the order of potentials such as
is on the order of potentials such as  , the square magnitude of the coordinate velocities of matter, etc.
, the square magnitude of the coordinate velocities of matter, etc. 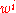 is the velocity vector of the PPN coordinate system relative to the mean rest-frame of the universe.
is the velocity vector of the PPN coordinate system relative to the mean rest-frame of the universe. 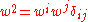 is the square magnitude of that velocity.
is the square magnitude of that velocity. 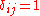 if and only if
if and only if  ,
,  otherwise.
otherwise.
There are ten metric potentials, ,
, 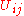 ,
,  ,
,  ,
,  ,
, 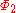 ,
, 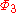 ,
,  ,
, 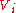 and
and  , one for each PPN parameter to ensure a unique solution. 10 linear equations in 10 unknowns are solved by inverting a 10 by 10 matrix. These metric potentials have forms such as:
, one for each PPN parameter to ensure a unique solution. 10 linear equations in 10 unknowns are solved by inverting a 10 by 10 matrix. These metric potentials have forms such as:
which is simply another way of writing the Newtonian gravitational potential.
A full list of metric potentials can be found in Misner et al. (1973), Will (1981, 1993, 2006) and in many other places.
Most metric theories of gravity can be lumped into categories. Scalar theories of gravitation
include conformally flat theories and stratified theories with time-orthogonal space slices.
In conformally flat theories such Nordström's theory of gravitation
the metric is given by and for this metric
and for this metric  , which violently disagrees with observations. In stratified theories such as Yilmaz theory of gravitation
, which violently disagrees with observations. In stratified theories such as Yilmaz theory of gravitation
the metric is given by and for this metric
and for this metric  , which also disagrees violently with observations.
, which also disagrees violently with observations.
Another class of theories is the quasilinear theories such as Whitehead's theory of gravitation
. For these . The relative magnitudes of the harmonics of the Earth's tides depend on
. The relative magnitudes of the harmonics of the Earth's tides depend on  and
and  , and measurements show that quasilinear theories disagree with observations of Earth's tides.
, and measurements show that quasilinear theories disagree with observations of Earth's tides.
Another class of metric theories is the bimetric theory
. For all of these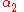 is non-zero. From the precession of the solar spin we know that
is non-zero. From the precession of the solar spin we know that 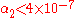 , and that effectively rules out bimetric theories.
, and that effectively rules out bimetric theories.
Another class of metric theories is the scalar tensor theories
, such as Brans-Dicke theory
. For all of these, . The limit of
. The limit of 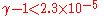 means that
means that  would have to be very large, so these theories are looking less and less likely as experimental accuracy improves.
would have to be very large, so these theories are looking less and less likely as experimental accuracy improves.
The final main class of metric theories is the vector-tensor theories. For all of these the gravitational "constant" varies with time and is non-zero. Lunar laser ranging experiments tightly constrain the variation of the gravitational "constant" with time and
is non-zero. Lunar laser ranging experiments tightly constrain the variation of the gravitational "constant" with time and 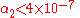 , so these theories are also looking unlikely.
, so these theories are also looking unlikely.
There are some metric theories of gravity that do not fit into the above categories, but they have similar problems.
† Will, C.M., Is momentum conserved? A test in the binary system PSR 1913 + 16, Astrophysical Journal, Part 2 - Letters (ISSN 0004-637X), vol. 393, no. 2, July 10, 1992, p. L59-L61.
‡ Based on from Will (1976, 2006). It is theoretically possible for an alternative model of gravity to bypass this bound, in which case the bound is
from Will (1976, 2006). It is theoretically possible for an alternative model of gravity to bypass this bound, in which case the bound is  from Ni (1972).
from Ni (1972).
The parameterized post-Newtonian formalism or PPN formalism is a version of this formulation that explicitly details the parameters in which a general theory of gravity can differ from Newtonian gravity. It is used as a tool to compare Newtonian and Einsteinian gravity in the limit in which the gravitational field
Gravitational field
The gravitational field is a model used in physics to explain the existence of gravity. In its original concept, gravity was a force between point masses...
is weak and generated by objects moving slowly compared to the speed of light
Speed of light
The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
. In general, PPN formalism can be applied to all metric theories of gravitation in which all bodies satisfy the Einstein equivalence principle (EEP). The speed of light remains constant in PPN formalism and it assumes that the metric tensor
Metric tensor (general relativity)
In general relativity, the metric tensor is the fundamental object of study. It may loosely be thought of as a generalization of the gravitational field familiar from Newtonian gravitation...
is always symmetric.
History
The earliest parameterizations of the post-Newtonian approximation were performed by Sir Arthur Stanley EddingtonArthur Stanley Eddington
Sir Arthur Stanley Eddington, OM, FRS was a British astrophysicist of the early 20th century. He was also a philosopher of science and a popularizer of science...
in 1922. However, they dealt solely with the vacuum gravitational field outside an isolated spherical body. Dr. Ken Nordtvedt
Ken Nordtvedt
Kenneth Leon Nordtvedt is a professor emeritus in the Physics Department at Montana State University and a senior researcher specializing in relativistic theories of gravity. He was born on April 16, 1939, in Chicago, Illinois. Nordtvedt graduated from the Massachusetts Institute of Technology and...
(1968, 1969) expanded this to include 7 parameters. Clifford Martin Will
Clifford Martin Will
Clifford Martin Will is a Canadian born mathematical physicist who is well known for his contributions to the theory of general relativity....
(1971) introduced a stressed, continuous matter description of celestial bodies.
The versions described here are based on Wei-Tou Ni
Wei-Tou Ni
Ni Wei-Tou is a Taiwanese physicist, who graduated from the Department of Physics of National Taiwan University , and got his PhD of Physics & Mathematics from California Institute of Technology...
(1972), Will and Nordtvedt (1972), Charles W. Misner
Charles W. Misner
Charles W. Misner is an American physicist and one of the authors of Gravitation. His specialties include general relativity and cosmology. His work has also provided early foundations for studies of quantum gravity and numerical relativity....
et al. (1973) (see Gravitation (book)
Gravitation (book)
In physics, Gravitation is a very important reference book on Einstein's theory of gravity by Charles W. Misner, Kip S. Thorne, and John Archibald Wheeler. Often considered the "Bible" of General Relativity by researchers for its prominence. It is frequently called MTW after its authors' initials....
), and Will (1981, 1993) and have 10 parameters.
Beta-delta notation
Ten post-Newtonian parameters completely characterize the weak-field behavior of the theory. The formalism has been a valuable tool in tests of general relativityTests of general relativity
At its introduction in 1915, the general theory of relativity did not have a solid empirical foundation. It was known that it correctly accounted for the "anomalous" precession of the perihelion of Mercury and on philosophical grounds it was considered satisfying that it was able to unify Newton's...
. In the notation of Will (1971), Ni (1972) and Misner et al. (1973) they have the following values:
 |
How much space curvature  is produced by unit rest mass ? is produced by unit rest mass ? |
 |
How much nonlinearity is there in the superposition law for gravity  ? ? |
 |
How much gravity is produced by unit kinetic energy  ? ? |
 |
How much gravity is produced by unit gravitational potential energy  ? ? |
 |
How much gravity is produced by unit internal energy 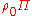 ? ? |
 |
How much gravity is produced by unit pressure 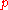 ? ? |
 |
Difference between radial and transverse kinetic energy on gravity |
 |
Difference between radial and transverse stress on gravity |
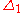 |
How much dragging of inertial frames  is produced by unit momentum is produced by unit momentum  ? ? |
 |
Difference between radial and transverse momentum on dragging of inertial frames |
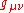 is the 4 by 4 symmetric metric tensor and indexes
is the 4 by 4 symmetric metric tensor and indexes  and
and  go from 1 to 3.
go from 1 to 3.In Einstein's theory, the values of these parameters are chosen (1) to fit Newton's Law of gravity in the limit of velocities and mass approaching zero, (2) to ensure conservation of energy, mass, momentum, and angular momentum, and (3) to make the equations independent of the reference frame. In this notation, general relativity has PPN parameters
 and
and 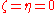
Alpha-zeta notation
In the more recent notation of Will & Nordtvedt (1972) and Will (1981, 1993, 2006) a different set of ten PPN parameters is used.





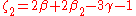


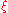 is calculated from
is calculated from 
The meaning of these is that
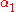 ,
,  and
and 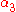 measure the extent of preferred frame effects.
measure the extent of preferred frame effects.  ,
,  ,
, 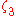 ,
,  and
and  measure the failure of conservation of energy, momentum and angular momentum.
measure the failure of conservation of energy, momentum and angular momentum.In this notation, general relativity has PPN parameters
 and
and 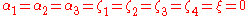
The mathematical relationship between the metric, metric potentials and PPN parameters for this notation is:

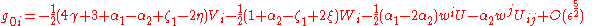

where repeated indexes are summed.
 is on the order of potentials such as
is on the order of potentials such as  , the square magnitude of the coordinate velocities of matter, etc.
, the square magnitude of the coordinate velocities of matter, etc. 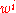 is the velocity vector of the PPN coordinate system relative to the mean rest-frame of the universe.
is the velocity vector of the PPN coordinate system relative to the mean rest-frame of the universe. 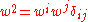 is the square magnitude of that velocity.
is the square magnitude of that velocity. 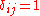 if and only if
if and only if  ,
,  otherwise.
otherwise.There are ten metric potentials,
 ,
, 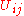 ,
,  ,
,  ,
,  ,
, 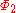 ,
, 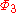 ,
,  ,
, 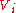 and
and  , one for each PPN parameter to ensure a unique solution. 10 linear equations in 10 unknowns are solved by inverting a 10 by 10 matrix. These metric potentials have forms such as:
, one for each PPN parameter to ensure a unique solution. 10 linear equations in 10 unknowns are solved by inverting a 10 by 10 matrix. These metric potentials have forms such as:
which is simply another way of writing the Newtonian gravitational potential.
A full list of metric potentials can be found in Misner et al. (1973), Will (1981, 1993, 2006) and in many other places.
How to apply PPN
Examples of the process of applying PPN formalism to alternative theories of gravity can be found in Will (1981, 1993). It is a nine step process:- Step 1: Identify the variables, which may include: (a) dynamical gravitational variables such as the metric
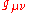 , scalar field
, scalar field 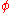 , vector field
, vector field  , tensor field
, tensor field  and so on; (b) prior-geometrical variables such as a flat background metric
and so on; (b) prior-geometrical variables such as a flat background metric  , cosmic time function
, cosmic time function  , and so on; (c) matter and non-gravitational field variables.
, and so on; (c) matter and non-gravitational field variables.
- Step 2: Set the cosmological boundary conditions. Assume a homogeneous isotropic cosmology, with isotropic coordinates in the rest frame of the universe. A complete cosmological solution may or may not be needed. Call the results
 ,
,  ,
, 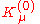 ,
, 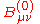 .
.
- Step 3: Get new variables from
 , with
, with  ,
,  or
or  if needed.
if needed.
- Step 4: Substitute these forms into the field equations, keeping only such terms as are necessary to obtain a final consistent solution for
 . Substitute the perfect fluid stress tensor for the matter sources.
. Substitute the perfect fluid stress tensor for the matter sources.
- Step 5: Solve for
 to
to  . Assuming this tends to zero far from the system, one obtains the form
. Assuming this tends to zero far from the system, one obtains the form 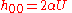 where
where  is the Newtonian gravitational potential and
is the Newtonian gravitational potential and  may be a complicated function including the gravitational "constant"
may be a complicated function including the gravitational "constant"  . The Newtonian metric has the form
. The Newtonian metric has the form 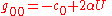 ,
,  ,
, 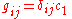 . Work in units where the gravitational "constant" measured today far from gravitating matter is unity so set
. Work in units where the gravitational "constant" measured today far from gravitating matter is unity so set  .
.
- Step 6: From linearized versions of the field equations solve for
 to
to 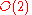 and
and 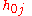 to
to 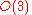 .
.
- Step 7: Solve for
 to
to 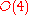 . This is the messiest step, involving all the nonlinearities in the field equations. The stress-energy tensor must also be expanded to sufficient order.
. This is the messiest step, involving all the nonlinearities in the field equations. The stress-energy tensor must also be expanded to sufficient order.
- Step 8: Convert to local quasi-Cartesian coordinates and to standard PPN gauge.
- Step 9: By comparing the result for
 with the equations presented in PPN with alpha-zeta parameters, read off the PPN parameter values.
with the equations presented in PPN with alpha-zeta parameters, read off the PPN parameter values.
Comparisons between theories of gravity
A table comparing PPN parameters for 23 theories of gravity can be found in Alternatives to general relativity#PPN parameters for a range of theories.Most metric theories of gravity can be lumped into categories. Scalar theories of gravitation
Scalar theories of gravitation
Scalar theories of gravitation are field theories of gravitation in which the gravitational field is described using a scalar field, which is required to satisfy some field equation....
include conformally flat theories and stratified theories with time-orthogonal space slices.
In conformally flat theories such Nordström's theory of gravitation
Nordström's theory of gravitation
In theoretical physics, Nordström's theory of gravitation was a predecessor of general relativity. Strictly speaking, there were actually two distinct theories proposed by the Finnish theoretical physicist Gunnar Nordström, in 1912 and 1913 respectively...
the metric is given by
 and for this metric
and for this metric  , which violently disagrees with observations. In stratified theories such as Yilmaz theory of gravitation
, which violently disagrees with observations. In stratified theories such as Yilmaz theory of gravitationYilmaz theory of gravitation
The Yilmaz theory of gravitation is an attempt by Huseyin Yilmaz and his coworkers to formulate a classical field theory of gravitation which is similar to general relativity in weak-field conditions, but in which event horizons cannot appear.Yilmaz's work has been criticized on various grounds,...
the metric is given by
 and for this metric
and for this metric  , which also disagrees violently with observations.
, which also disagrees violently with observations.Another class of theories is the quasilinear theories such as Whitehead's theory of gravitation
Whitehead's theory of gravitation
In theoretical physics, Whitehead's theory of gravitation was introduced by the distinguished mathematician and philosopher Alfred North Whitehead in 1922.-Principal features of the theory:Whitehead's theory is said to feature a prior geometry...
. For these
 . The relative magnitudes of the harmonics of the Earth's tides depend on
. The relative magnitudes of the harmonics of the Earth's tides depend on  and
and  , and measurements show that quasilinear theories disagree with observations of Earth's tides.
, and measurements show that quasilinear theories disagree with observations of Earth's tides.Another class of metric theories is the bimetric theory
Bimetric theory
Bimetric theory refers to a class of modified theories of gravity in which two metric tensors are used instead of one. Often the second metric is introduced at high energies, with the implication that the speed of light may be energy dependent....
. For all of these
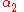 is non-zero. From the precession of the solar spin we know that
is non-zero. From the precession of the solar spin we know that 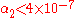 , and that effectively rules out bimetric theories.
, and that effectively rules out bimetric theories.Another class of metric theories is the scalar tensor theories
Scalar-tensor theory
In theoretical physics, a scalar-tensor theory is a theory that includes both a scalar field and a tensor field to represent a certain interaction...
, such as Brans-Dicke theory
Brans-Dicke theory
In theoretical physics, the Brans–Dicke theory of gravitation is a theoretical framework to explain gravitation. It is a well-known competitor of Einstein's more popular theory of general relativity...
. For all of these,
 . The limit of
. The limit of 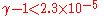 means that
means that  would have to be very large, so these theories are looking less and less likely as experimental accuracy improves.
would have to be very large, so these theories are looking less and less likely as experimental accuracy improves.The final main class of metric theories is the vector-tensor theories. For all of these the gravitational "constant" varies with time and
 is non-zero. Lunar laser ranging experiments tightly constrain the variation of the gravitational "constant" with time and
is non-zero. Lunar laser ranging experiments tightly constrain the variation of the gravitational "constant" with time and 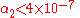 , so these theories are also looking unlikely.
, so these theories are also looking unlikely.There are some metric theories of gravity that do not fit into the above categories, but they have similar problems.
Accuracy from experimental tests
Bounds on the PPN parameters Will (2006)| Parameter | Bound | Effects | Experiment |
|---|---|---|---|
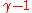 |
 x x  |
Time delay, Light deflection | Cassini tracking |
 |
 x x  |
Nordtvedt effect, Perihelion shift | Nordtvedt effect Nordtvedt effect In theoretical astrophysics, the Nordtvedt effect refers to the relative motion between the Earth and the Moon which would be observed if the gravitational self-energy of a body contributed to its gravitational mass but not its inertial mass... |
 |
 |
Earth tides | Gravimeter data |
 |
 |
Orbit polarization | Lunar laser ranging Lunar laser ranging experiment The ongoing Lunar Laser Ranging Experiment measures the distance between the Earth and the Moon using laser ranging. Lasers on Earth are aimed at retroreflectors planted on the moon during the Apollo program, and the time for the reflected light to return is determined... |
 |
 x x  |
Spin precession | Sun axis' alignment with ecliptic |
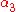 |
 x x  |
Self-acceleration | Pulsar spin-down statistics |
 |
 |
- | Combined PPN bounds |
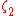 |
 x x  † † |
Binary pulsar acceleration | PSR 1913+16 PSR 1913+16 PSR B1913+16 is a pulsar which together with another neutron star is in orbit around a common center of mass, thus forming a binary star system. In 1974 it was discovered by Russell Alan Hulse and Joseph Hooton Taylor, Jr., of Princeton University... |
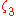 |
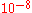 |
Newton's 3rd law | Lunar acceleration |
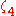 |
 ‡ ‡ |
- | Kreuzer experiment |
† Will, C.M., Is momentum conserved? A test in the binary system PSR 1913 + 16, Astrophysical Journal, Part 2 - Letters (ISSN 0004-637X), vol. 393, no. 2, July 10, 1992, p. L59-L61.
‡ Based on
 from Will (1976, 2006). It is theoretically possible for an alternative model of gravity to bypass this bound, in which case the bound is
from Will (1976, 2006). It is theoretically possible for an alternative model of gravity to bypass this bound, in which case the bound is  from Ni (1972).
from Ni (1972).See also
- Alternatives to general relativity#PPN parameters for a range of theories
- Linearized gravityLinearized gravityLinearized gravity is an approximation scheme in general relativity in which the nonlinear contributions from the spacetime metric are ignored, simplifying the study of many problems while still producing useful approximate results.-The method:...
- Peskin-Takeuchi parameterPeskin-Takeuchi parameterIn particle physics, the Peskin–Takeuchi parameters are a set of three measurable quantities, called S, T, and U, that parameterize potential new physics contributions to electroweak radiative corrections...
The same thing as PPN, but for electroweak theory instead of gravitationGravitationGravitation, or gravity, is a natural phenomenon by which physical bodies attract with a force proportional to their mass. Gravitation is most familiar as the agent that gives weight to objects with mass and causes them to fall to the ground when dropped... - Tests of general relativityTests of general relativityAt its introduction in 1915, the general theory of relativity did not have a solid empirical foundation. It was known that it correctly accounted for the "anomalous" precession of the perihelion of Mercury and on philosophical grounds it was considered satisfying that it was able to unify Newton's...

