Kepler-Poinsot solid
Encyclopedia
In geometry
, a Kepler–Poinsot polyhedron is any of four regular
star polyhedra
. They may be obtained by stellating
the regular convex dodecahedron and icosahedron
, and differ from these in having regular pentagram
mic faces or vertex figure
s.
The four Kepler–Poinsot polyhedra are illustrated above. Each is identified by its Schläfli symbol, of the form {p, q}, and by its name. One face of each figure is shown yellow and outlined in red.
s (star pentagons) as faces or vertex figures. The small and great stellated dodecahedron have nonconvex regular pentagram
faces. The great dodecahedron and great icosahedron have convex
polygonal faces, but pentagrammic vertex figure
s.
In all cases, two faces can intersect along a line that is not an edge of either face, so that part of each face passes through the interior of the figure. Such lines of intersection are not part of the polyhedral structure and are sometimes called false edges. Likewise where three such lines intersect at a point that is not a corner of any face, these points are false vertices. The images below show golden balls at the true vertices, and silver rods along the true edges.
For example the small stellated dodecahedron has 12 pentagram
faces with the central pentagon
al part hidden inside the solid. The visible parts of each face comprise five isosceles triangles which touch at five points around the pentagon. We could treat these triangles as 60 separate faces to obtain a new, irregular polyhedron which looks outwardly identical. Each edge would now be divided into three shorter edges (of two different kinds), and the 20 false vertices would become true ones, so that we have a total of 32 vertices (again of two kinds). The hidden inner pentagons are no longer part of the polyhedral surface, and can disappear. Now the Euler relation holds: 60 − 90 + 32 = 2. However this polyhedron is no longer the one described by the Schläfli symbol {5/2, 5}, and so can not be a Kepler–Poinsot solid even though it still looks like one from outside.
does not always hold. Schläfli held that all polyhedra must have χ = 2, and he rejected the small stellated dodecahedron and great dodecahedron as proper polyhedra. This view was never widely held.
A modified form of Euler's formula, using polyhedral density (D) and polygon density of the vertex figure
s (
) and faces (
) was given by Arthur Cayley
, and holds both for convex polyhedra (where the correction factors are all 1), and the Kepler–Poinsot polyhedra:
pairs:
The small stellated dodecahedron and great icosahedron share the same vertices and edges. The icosahedron and great dodecahedron also share the same vertices and edges.
The three dodecahedra are all stellation
s of the regular convex dodecahedron, and the great icosahedron is a stellation
of the regular convex icosahedron. The small stellated dodecahedron and the great icosahedron are facetting
s of the convex dodecahedron, while the two great dodecahedra are facetting
s of the regular convex icosahedron.
If the intersections are treated as new edges and vertices, the figures obtained will not be regular
, but they can still be considered stellation
s. (See also List of Wenninger polyhedron models)
, Italy
. It dates from the 15th century and is sometimes attributed to Paolo Uccello
. In his Perspectiva corporum regularium (Perspectives of the regular solids) http://www.mathe.tu-freiberg.de/~hebisch/cafe/jamnitzer/galerie7a.html, a book of woodcuts published in the 16th century, Wenzel Jamnitzer
depicts the great dodecahedron and the great stellated dodecahedron. It is clear from the general arrangement of the book that he regards only the five Platonic solids as regular, and does not understand the regular nature of his great dodecahedra.
The small and great stellated dodecahedra, sometimes called the Kepler polyhedra, were first recognized as regular by Johannes Kepler
in 1619. He obtained them by stellating
the regular convex dodecahedron, for the first time treating it as a surface rather than a solid. He noticed that by extending the edges or faces of the convex dodecahedron until they met again, he could obtain star pentagons. Further, he recognized that these star pentagons are also regular. In this way he constructed the two stellated dodecahedra. Each has the central convex region of each face "hidden" within the interior, with only the triangular arms visible. Kepler's final step was to recognize that these polyhedra fit the definition of regularity, even though they were not convex, as the traditional Platonic solid
s were.
In 1809, Louis Poinsot
rediscovered Kepler's figures, by assembling star pentagons around each vertex. He also assembled convex polygons around star vertices to discover two more regular stars, the great icosahedron and great dodecahedron. Some people call these two the Poinsot polyhedra. Poinsot did not know if he had discovered all the regular star polyhedra.
Three years later, Augustin Cauchy proved the list complete by stellating
the Platonic solid
s, and almost half a century after that, in 1858, Bertrand
provided a more elegant proof by facetting
them.
The following year, Arthur Cayley
gave the Kepler–Poinsot polyhedra the names by which they are generally known today.
A hundred years later, John Conway
developed a systematic terminology for stellations in up to four dimensions. Within this scheme, he suggested slightly modified names for two of the regular star polyhedra:
Conway's names have seen some use but have not been widely adopted.
Regular star polyhedra first appear in Renaissance art. A small stellated dodecahedron is depicted in a marble tarsia on the floor of St. Mark's Basilica, Venice, Italy, dating from ca. 1430 and sometimes attributed to Paulo Ucello. Wenzel Jamnitzer published his book of woodcuts Perspectiva Corporum Regularium in 1568. He depicts the great dodecahedron and the great stellated dodecahedron - this second is slightly distorted, probably through errors in method rather than ignorance of the form. However there is no evidence that these artists understood the regularity of such figures.
In the 20th Century, Artist M. C. Escher
's interest in geometric forms often led to works based on or including regular solids; Gravitation
is based on a small stellated dodecahedron.
A dissection
of the great dodecahedron was used for the 1980s puzzle Alexander's Star
.
Norwegian artist Vebjørn Sand
s sculpture The Kepler Star is displayed near Oslo Airport, Gardermoen
. The star spans 14 meters, and consists of an icosahedron
and a dodecahedron inside a great stellated dodecahedron.
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, a Kepler–Poinsot polyhedron is any of four regular
Regular polyhedron
A regular polyhedron is a polyhedron whose faces are congruent regular polygons which are assembled in the same way around each vertex. A regular polyhedron is highly symmetrical, being all of edge-transitive, vertex-transitive and face-transitive - i.e. it is transitive on its flags...
star polyhedra
Star polyhedron
In geometry, a star polyhedron is a polyhedron which has some repetitive quality of nonconvexity giving it a star-like visual quality.There are two general kinds of star polyhedron:*Polyhedra which self-intersect in a repetitive way....
. They may be obtained by stellating
Stellation
Stellation is a process of constructing new polygons , new polyhedra in three dimensions, or, in general, new polytopes in n dimensions. The process consists of extending elements such as edges or face planes, usually in a symmetrical way, until they meet each other again...
the regular convex dodecahedron and icosahedron
Icosahedron
In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids....
, and differ from these in having regular pentagram
Pentagram
A pentagram is the shape of a five-pointed star drawn with five straight strokes...
mic faces or vertex figure
Vertex figure
In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:...
s.
Identification
The four Kepler–Poinsot polyhedra are illustrated above. Each is identified by its Schläfli symbol, of the form {p, q}, and by its name. One face of each figure is shown yellow and outlined in red.
Non-convexity
These figures have pentagramPentagram
A pentagram is the shape of a five-pointed star drawn with five straight strokes...
s (star pentagons) as faces or vertex figures. The small and great stellated dodecahedron have nonconvex regular pentagram
Pentagram
A pentagram is the shape of a five-pointed star drawn with five straight strokes...
faces. The great dodecahedron and great icosahedron have convex
Convex polygon
In geometry, a polygon can be either convex or concave .- Convex polygons :A convex polygon is a simple polygon whose interior is a convex set...
polygonal faces, but pentagrammic vertex figure
Vertex figure
In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:...
s.
In all cases, two faces can intersect along a line that is not an edge of either face, so that part of each face passes through the interior of the figure. Such lines of intersection are not part of the polyhedral structure and are sometimes called false edges. Likewise where three such lines intersect at a point that is not a corner of any face, these points are false vertices. The images below show golden balls at the true vertices, and silver rods along the true edges.
For example the small stellated dodecahedron has 12 pentagram
Pentagram
A pentagram is the shape of a five-pointed star drawn with five straight strokes...
faces with the central pentagon
Pentagon
In geometry, a pentagon is any five-sided polygon. A pentagon may be simple or self-intersecting. The sum of the internal angles in a simple pentagon is 540°. A pentagram is an example of a self-intersecting pentagon.- Regular pentagons :In a regular pentagon, all sides are equal in length and...
al part hidden inside the solid. The visible parts of each face comprise five isosceles triangles which touch at five points around the pentagon. We could treat these triangles as 60 separate faces to obtain a new, irregular polyhedron which looks outwardly identical. Each edge would now be divided into three shorter edges (of two different kinds), and the 20 false vertices would become true ones, so that we have a total of 32 vertices (again of two kinds). The hidden inner pentagons are no longer part of the polyhedral surface, and can disappear. Now the Euler relation holds: 60 − 90 + 32 = 2. However this polyhedron is no longer the one described by the Schläfli symbol {5/2, 5}, and so can not be a Kepler–Poinsot solid even though it still looks like one from outside.
Euler characteristic χ
A Kepler–Poinsot polyhedron covers its circumscribed sphere more than once, with the centers of faces acting as winding points in the figures which have pentagrammic faces, and the vertices in the others. Because of this, they are not necessarily topologically equivalent to the sphere as Platonic solids are, and in particular the Euler relationEuler characteristic
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...
does not always hold. Schläfli held that all polyhedra must have χ = 2, and he rejected the small stellated dodecahedron and great dodecahedron as proper polyhedra. This view was never widely held.
A modified form of Euler's formula, using polyhedral density (D) and polygon density of the vertex figure
Vertex figure
In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:...
s (
) and faces () was given by Arthur CayleyArthur Cayley
Arthur Cayley F.R.S. was a British mathematician. He helped found the modern British school of pure mathematics....
, and holds both for convex polyhedra (where the correction factors are all 1), and the Kepler–Poinsot polyhedra:
Duality
The Kepler–Poinsot polyhedra exist in dualDual polyhedron
In geometry, polyhedra are associated into pairs called duals, where the vertices of one correspond to the faces of the other. The dual of the dual is the original polyhedron. The dual of a polyhedron with equivalent vertices is one with equivalent faces, and of one with equivalent edges is another...
pairs:
- Small stellated dodecahedron and great dodecahedron.
- Great stellated dodecahedron and great icosahedron.
Summary
| Name | Picture | Spherical tiling |
Stellation Stellation Stellation is a process of constructing new polygons , new polyhedra in three dimensions, or, in general, new polytopes in n dimensions. The process consists of extending elements such as edges or face planes, usually in a symmetrical way, until they meet each other again... diagram |
Schläfli {p,q} and Coxeter-Dynkin Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... |
Faces {p} |
Edges | Vertices {q} verf. Vertex figure In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:... |
χ Euler characteristic In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent... |
Density | Symmetry Symmetry group The symmetry group of an object is the group of all isometries under which it is invariant with composition as the operation... |
Dual Dual polyhedron In geometry, polyhedra are associated into pairs called duals, where the vertices of one correspond to the faces of the other. The dual of the dual is the original polyhedron. The dual of a polyhedron with equivalent vertices is one with equivalent faces, and of one with equivalent edges is another... |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Small stellated dodecahedron |  |
 |
 |
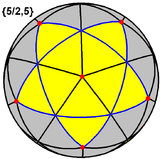{5/2,5} |
12 {5/2}  |
30 | 12 {5}  |
-6 | 3 | Ih | Great dodecahedron |
| Great dodecahedron |  |
 |
 |
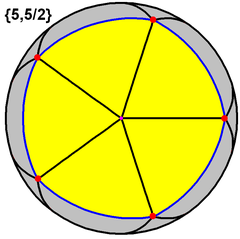{5,5/2} |
12 {5} |
30 | 12 {5/2} |
-6 | 3 | Ih | Small stellated dodecahedron |
| Great stellated dodecahedron |  |
 |
 |
{5/2,3} |
12 {5/2} |
30 | 20 {3}  |
2 | 7 | Ih | Great icosahedron |
| Great icosahedron |  |
 |
 |
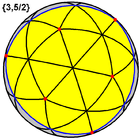{3,5/2} |
20 {3} |
30 | 12 {5/2} |
2 | 7 | Ih | Great stellated dodecahedron |
Relationships among the regular polyhedra
| These share the same vertex arrangement Vertex arrangement In geometry, a vertex arrangement is a set of points in space described by their relative positions. They can be described by their use in polytopes.... s: |
These share the same vertex Vertex arrangement In geometry, a vertex arrangement is a set of points in space described by their relative positions. They can be described by their use in polytopes.... and edge arrangements: |
|---|---|
 The icosahedron Icosahedron In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids.... , small stellated dodecahedron, great icosahedron, and great dodecahedron. |
The small stellated dodecahedron and great icosahedron. |
 The dodecahedron and great stellated dodecahedron. |
The icosahedron Icosahedron In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids.... and great dodecahedron. |
The small stellated dodecahedron and great icosahedron share the same vertices and edges. The icosahedron and great dodecahedron also share the same vertices and edges.
The three dodecahedra are all stellation
Stellation
Stellation is a process of constructing new polygons , new polyhedra in three dimensions, or, in general, new polytopes in n dimensions. The process consists of extending elements such as edges or face planes, usually in a symmetrical way, until they meet each other again...
s of the regular convex dodecahedron, and the great icosahedron is a stellation
Stellation
Stellation is a process of constructing new polygons , new polyhedra in three dimensions, or, in general, new polytopes in n dimensions. The process consists of extending elements such as edges or face planes, usually in a symmetrical way, until they meet each other again...
of the regular convex icosahedron. The small stellated dodecahedron and the great icosahedron are facetting
Facetting
In geometry, facetting is the process of removing parts of a polygon, polyhedron or polytope, without creating any new vertices.Facetting is the reciprocal or dual process to stellation...
s of the convex dodecahedron, while the two great dodecahedra are facetting
Facetting
In geometry, facetting is the process of removing parts of a polygon, polyhedron or polytope, without creating any new vertices.Facetting is the reciprocal or dual process to stellation...
s of the regular convex icosahedron.
If the intersections are treated as new edges and vertices, the figures obtained will not be regular
Regular polyhedron
A regular polyhedron is a polyhedron whose faces are congruent regular polygons which are assembled in the same way around each vertex. A regular polyhedron is highly symmetrical, being all of edge-transitive, vertex-transitive and face-transitive - i.e. it is transitive on its flags...
, but they can still be considered stellation
Stellation
Stellation is a process of constructing new polygons , new polyhedra in three dimensions, or, in general, new polytopes in n dimensions. The process consists of extending elements such as edges or face planes, usually in a symmetrical way, until they meet each other again...
s. (See also List of Wenninger polyhedron models)
History
Most, if not all, of the Kepler-Poinsot polyhedra were known of in some form or other before Kepler. A small stellated dodecahedron appears in a marble tarsia (inlay panel) on the floor of St. Mark's Basilica, VeniceVenice
Venice is a city in northern Italy which is renowned for the beauty of its setting, its architecture and its artworks. It is the capital of the Veneto region...
, Italy
Italy
Italy , officially the Italian Republic languages]] under the European Charter for Regional or Minority Languages. In each of these, Italy's official name is as follows:;;;;;;;;), is a unitary parliamentary republic in South-Central Europe. To the north it borders France, Switzerland, Austria and...
. It dates from the 15th century and is sometimes attributed to Paolo Uccello
Paolo Uccello
Paolo Uccello , born Paolo di Dono, was an Italian painter and a mathematician who was notable for his pioneering work on visual perspective in art. Giorgio Vasari in his book Lives of the Artists wrote that Uccello was obsessed by his interest in perspective and would stay up all night in his...
. In his Perspectiva corporum regularium (Perspectives of the regular solids) http://www.mathe.tu-freiberg.de/~hebisch/cafe/jamnitzer/galerie7a.html, a book of woodcuts published in the 16th century, Wenzel Jamnitzer
Wenzel Jamnitzer
Wenzel Jamnitzer was a Northern Mannerist goldsmith, artist, and printmaker in etching, who worked in Nuremberg...
depicts the great dodecahedron and the great stellated dodecahedron. It is clear from the general arrangement of the book that he regards only the five Platonic solids as regular, and does not understand the regular nature of his great dodecahedra.
The small and great stellated dodecahedra, sometimes called the Kepler polyhedra, were first recognized as regular by Johannes Kepler
Johannes Kepler
Johannes Kepler was a German mathematician, astronomer and astrologer. A key figure in the 17th century scientific revolution, he is best known for his eponymous laws of planetary motion, codified by later astronomers, based on his works Astronomia nova, Harmonices Mundi, and Epitome of Copernican...
in 1619. He obtained them by stellating
Stellation
Stellation is a process of constructing new polygons , new polyhedra in three dimensions, or, in general, new polytopes in n dimensions. The process consists of extending elements such as edges or face planes, usually in a symmetrical way, until they meet each other again...
the regular convex dodecahedron, for the first time treating it as a surface rather than a solid. He noticed that by extending the edges or faces of the convex dodecahedron until they met again, he could obtain star pentagons. Further, he recognized that these star pentagons are also regular. In this way he constructed the two stellated dodecahedra. Each has the central convex region of each face "hidden" within the interior, with only the triangular arms visible. Kepler's final step was to recognize that these polyhedra fit the definition of regularity, even though they were not convex, as the traditional Platonic solid
Platonic solid
In geometry, a Platonic solid is a convex polyhedron that is regular, in the sense of a regular polygon. Specifically, the faces of a Platonic solid are congruent regular polygons, with the same number of faces meeting at each vertex; thus, all its edges are congruent, as are its vertices and...
s were.
In 1809, Louis Poinsot
Louis Poinsot
Louis Poinsot was a French mathematician and physicist. Poinsot was the inventor of geometrical mechanics, showing how a system of forces acting on a rigid body could be resolved into a single force and a couple.-Life:...
rediscovered Kepler's figures, by assembling star pentagons around each vertex. He also assembled convex polygons around star vertices to discover two more regular stars, the great icosahedron and great dodecahedron. Some people call these two the Poinsot polyhedra. Poinsot did not know if he had discovered all the regular star polyhedra.
Three years later, Augustin Cauchy proved the list complete by stellating
Stellation
Stellation is a process of constructing new polygons , new polyhedra in three dimensions, or, in general, new polytopes in n dimensions. The process consists of extending elements such as edges or face planes, usually in a symmetrical way, until they meet each other again...
the Platonic solid
Platonic solid
In geometry, a Platonic solid is a convex polyhedron that is regular, in the sense of a regular polygon. Specifically, the faces of a Platonic solid are congruent regular polygons, with the same number of faces meeting at each vertex; thus, all its edges are congruent, as are its vertices and...
s, and almost half a century after that, in 1858, Bertrand
Joseph Louis François Bertrand
Joseph Louis François Bertrand was a French mathematician who worked in the fields of number theory, differential geometry, probability theory, economics and thermodynamics....
provided a more elegant proof by facetting
Facetting
In geometry, facetting is the process of removing parts of a polygon, polyhedron or polytope, without creating any new vertices.Facetting is the reciprocal or dual process to stellation...
them.
The following year, Arthur Cayley
Arthur Cayley
Arthur Cayley F.R.S. was a British mathematician. He helped found the modern British school of pure mathematics....
gave the Kepler–Poinsot polyhedra the names by which they are generally known today.
A hundred years later, John Conway
John Horton Conway
John Horton Conway is a prolific mathematician active in the theory of finite groups, knot theory, number theory, combinatorial game theory and coding theory...
developed a systematic terminology for stellations in up to four dimensions. Within this scheme, he suggested slightly modified names for two of the regular star polyhedra:
| Cayley's name | Conway's name |
| small stellated dodecahedron | stellated dodecahedron |
| great dodecahedron | great dodecahedron (unchanged) |
| great stellated dodecahedron | stellated great dodecahedron |
| great icosahedron | great icosahedron (unchanged) |
Conway's names have seen some use but have not been widely adopted.
Regular star polyhedra in art and culture
In the 20th Century, Artist M. C. Escher
M. C. Escher
Maurits Cornelis Escher , usually referred to as M. C. Escher , was a Dutch graphic artist. He is known for his often mathematically inspired woodcuts, lithographs, and mezzotints...
's interest in geometric forms often led to works based on or including regular solids; Gravitation
Gravitation (M. C. Escher)
Gravitation is a mixed media work by the Dutch artist M. C. Escher which was completed in June, 1952. It was first printed as a black-and-white lithograph and then coloured by hand in watercolour....
is based on a small stellated dodecahedron.
A dissection
Dissection (geometry)
In geometry, a dissection problem is the problem of partitioning a geometric figure into smaller pieces that may be rearranged into a new figure of equal content. In this context, the partitioning is called simply a dissection...
of the great dodecahedron was used for the 1980s puzzle Alexander's Star
Alexander's Star
Alexander's Star is a puzzle similar to the Rubik's Cube, in the shape of a great dodecahedron.-History:Alexander's Star was invented by Adam Alexander, an American mathematician, in 1982...
.
Norwegian artist Vebjørn Sand
Vebjørn Sand
Vebjørn Sand is a Norwegian painter and artist. He is known for his paintings as well as his public arts projects, such as the Da Vinci Project, and the Kepler star monument at Oslo Airport, Gardermoen. Sand attended a Steiner school.-External links:* *...
s sculpture The Kepler Star is displayed near Oslo Airport, Gardermoen
Oslo Airport, Gardermoen
Oslo Airport, Gardermoen is the principal airport serving Oslo, Norway. It acts as the main domestic hub and international airport for Norway, and the second-busiest airport in the Nordic countries. A hub for Scandinavian Airlines and Norwegian Air Shuttle, and a focus city for Widerøe, it is...
. The star spans 14 meters, and consists of an icosahedron
Icosahedron
In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids....
and a dodecahedron inside a great stellated dodecahedron.
See also
- Regular polytopeRegular polytopeIn mathematics, a regular polytope is a polytope whose symmetry is transitive on its flags, thus giving it the highest degree of symmetry. All its elements or j-faces — cells, faces and so on — are also transitive on the symmetries of the polytope, and are regular polytopes of...
- Regular polyhedronRegular polyhedronA regular polyhedron is a polyhedron whose faces are congruent regular polygons which are assembled in the same way around each vertex. A regular polyhedron is highly symmetrical, being all of edge-transitive, vertex-transitive and face-transitive - i.e. it is transitive on its flags...
- List of regular polytopes
- Uniform polyhedronUniform polyhedronA uniform polyhedron is a polyhedron which has regular polygons as faces and is vertex-transitive...
- Polyhedral compoundPolyhedral compoundA polyhedral compound is a polyhedron that is itself composed of several other polyhedra sharing a common centre. They are the three-dimensional analogs of polygonal compounds such as the hexagram....
- Schläfli–Hess polychoron The 10 4-dimensional star polytopes
External links
- Paper models of Kepler–Poinsot polyhedra
- Free paper models (nets) of Kepler–Poinsot polyhedra
- The Uniform Polyhedra
- VRML models of the Kepler–Poinsot polyhedra
- Stellation and facetting - a brief history
- Stella: Polyhedron Navigator: Software used to create many of the images on this page.