Kakutani fixed point theorem
Encyclopedia
In mathematical analysis
, the Kakutani fixed-point theorem is a fixed-point theorem
for set-valued functions. It provides sufficient conditions for a set-valued function defined on a convex
, compact subset of a Euclidean space
to have a fixed point
, i.e. a point which is map
ped to a set containing it. The Kakutani fixed point theorem is a generalization of Brouwer fixed point theorem
. The Brouwer fixed point theorem is a fundamental result in topology
which proves the existence of fixed points for continuous functions defined on compact, convex subsets of Euclidean spaces. Kakutani's theorem extends this to set-valued functions.
The theorem was developed by Shizuo Kakutani
in 1941 and was famously used by John Nash
in his description of Nash equilibrium
. It has subsequently found widespread application in game theory
and economics
.
When we say that the graph of
is closed, we mean that for all sequences 
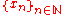and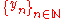 
such that 
, 
and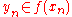 
for all 
, we have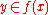 
.
from X to the power set of Y, written as φ: X→2Y. Some prefer the term correspondence, which is used to refer to a function that for each input may return many outputs. Thus, each element of the domain corresponds to a subset of one or more elements of the range.
Closed graph: A set-valued function φ: X→2Y is said to have a closed graph if the set {(x,y)| y ∈ φ(x)} is a closed
subset of X×Y in the product topology
.
Fixed point: Let φ: X→2X be a set-valued function. Then a ∈ X is a fixed point of φ if a ∈ φ(a).
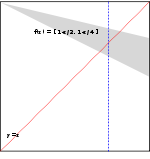Let f(x) be a set-valued function defined on the closed interval
[0, 1] that maps a point x to the closed interval [1 − x/2, 1 − x/4]. Then f(x) satisfies all the assumptions of the theorem and must have fixed points.
In the diagram, any point on the 45° line (dotted line in red) which intersects the graph of the function (shaded in grey) is a fixed point, so in fact there is an infinity of fixed points in this particular case. For example, x = 0.72 (dashed line in blue) is a fixed point since 0.72 ∈ [1 − 0.72/2, 1 − 0.72/4].
The requirement that φ(x) be convex for all x is essential for the theorem to hold.
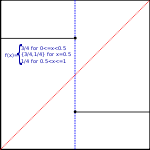
Consider the following function defined on [0,1]: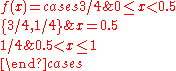
The function has no fixed point. Though it satisfies all other requirements of Kakutani's theorem, its value fails to be convex at x = 0.5.
, compact and convex
subset
of some Euclidean space
Rn. Let φ: S→2S be an upper hemicontinuous set-valued function on S with the property that φ(x) is non-empty, closed
and convex for all x ∈ S. Then φ has a fixed point
.
This statement of Kakutani's theorem is completely equivalent to the statement given at the beginning of this article.
We can show this by using the Closed graph theorem
for set-valued functions, which says that a for a compact Hausdorff
range space Y, a set-valued function φ: X→2Y has a closed graph if and only if it is upper hemicontinuous and φ(x) is a closed set for all x. Since all Euclidean space
s are Hausdorff (being metric space
s) and φ is required to be closed-valued in the alternative statement of the Kakutani theorem, the Closed Graph Theorem implies that the two statements are equivalent.
used the Kakutani fixed point theorem to prove a major result in game theory
.
Stated informally, the theorem implies the existence of a Nash equilibrium
in every finite game with mixed strategies for any number of players. This work would later earn him a Nobel Prize in Economics.
In this case, S is the set of tuple
s of mixed strategies chosen by each player in a game. The function φ(x) gives a new tuple where each player's strategy is her best response to other players' strategies in x. Since there may be a number of responses which are equally good, φ is set-valued rather than single-valued. Then the Nash equilibrium
of the game is defined as a fixed point of φ, i.e. a tuple of strategies where each player's strategy is a best response to the strategies of the other players. Kakutani's theorem ensures that this fixed point exists.
theory in economics, Kakutani's theorem has been used to prove the existence of set of prices which simultaneously equate supply with demand in all markets of an economy. The existence of such prices had been an open question in economics going back to at least Walras
. The first proof of this result was constructed by Lionel McKenzie.
In this case, S is the set of tuple
s of commodity prices. φ(x) is chosen as a function whose result is different from its arguments as long as the price-tuple x does not equate supply and demand everywhere. The challenge here is to construct φ so that it has this property while at the same time satisfying the conditions in Kakutani's theorem. If this can be done then φ has a fixed point according to the theorem. Given the way it was constructed, this fixed point must correspond to a price-tuple which equates supply with demand everywhere.
S =
The proof of Kakutani's theorem is simplest for set-valued functions defined over closed intervals
of the real line. However, the proof of this case is instructive since its general strategy can be carried over to the higher dimensional case as well.
Let φ:[0,1] →2[0,1] be a set-valued function on the closed interval [0,1] which satisfies the conditions of Kakutani's fixed-point theorem.
Let (ai, bi, pi, qi) for i = 0, 1, … be a sequence
with the following properties:
Thus, the closed intervals[ ai, bi] form a sequence of subintervals of [0,1] . Condition (2) tells us that these subintervals continue to become smaller while condition (3)–(6) tell us that the function φ shifts the left end of each subinterval to its right and shifts the right end of each subinterval to its left.
Such a sequence can be constructed as follows. Let a0 = 0 and b0 = 1. Let p0 be any point in φ(0) and q0 be any point in φ(1). Then, conditions (1)–(4) are immediately fulfilled. Moreover, since p0 ∈ φ(0) ⊂[0,1] , it must be the case that p0 ≥ 0 and hence condition (5) is fulfilled. Similarly condition (6) is fulfilled by q0.
Now suppose we have chosen ak, bk, pk and qk satisfying (1)–(6). Let,
Then m ∈[0,1] because [0,1] is convex
.
If there is a r ∈ φ(m) such that r ≥ m, then we take,
Otherwise, since φ(m) is non-empty, there must be a s ∈ φ(m) such that s ≤ m. In this case let,
It can be verified that ak+1, bk+1, pk+1 and qk+1 satisfy conditions (1)–(6).
The cartesian product
[0,1] ×[0,1] ×[0,1] ×[0,1] is a compact set by Tychonoff's theorem
. Since the sequence (an, pn, bn, qn) lies in this compact set, it must have a convergent
subsequence
by the Bolzano-Weierstrass theorem. Let's fix attention on such a subsequence and let its limit be (a*, p*,b*,q*). Since the graph of φ is closed it must be the case that p* ∈ φ(a*) and q* ∈ φ(b*). Moreover, by condition (5), p* ≥ a* and by condition (6), q* ≤ b*.
But since (bi − ai) ≤ 2−i by condition (2),
So, b* equals a*. Let x = b* = a*.
Then we have the situation that
If p* = q* then p* = x = q*. Since p* ∈ φ(x), x is a fixed point of φ.
Otherwise, since φ(x) is convex
and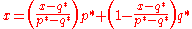
it once again follows that x must belong to φ(x) since p* and q* do and hence x is a fixed point of φ.
are the simplest objects on which Kakutani's theorem can be proved. Informally, a n-simplex is the higher dimensional version of a triangle. Proving Kakutani's theorem for set-valued function defined on a simplex is not essentially different from proving it for intervals. The additional complexity in the higher-dimensional case exists in the first step of chopping up the domain into finer subpieces:
Once these changes have been made to the first step, the second and third steps of finding a limiting point and proving that it is a fixed point are almost unchanged from the one-dimensional case.
. Then we can apply the already established result for n-simplices.
s by Irving Glicksberg
and Ky Fan
.
To state the theorem in this case, we need a few more definitions:
Upper semicontinuity: A set-valued function φ: X→2Y is upper semicontinuous if for every open set
W ⊂ Y, the set {x| φ(x) ⊂ W} is open in X.
Kakutani map: Let X and Y be topological vector space
s and φ: X→2Y be a set-valued function. If Y is convex, then φ is termed a Kakutani map if it is upper semicontinuous and φ(x) is non-empty, compact and convex for all x ∈ X.
Then the Kakutani-Glicksberg-Fan theorem can be stated as:
The corresponding result for single-valued functions is the Tychonoff fixed point theorem.
If the space on which the function is defined is Hausdorff
in addition to being locally convex, then the statement of the theorem becomes the same as that in the Euclidean
case:
Ken Binmore recalls that Kakutani once asked him at a conference why so many economists had attended his talk. When Binmore told him that it was probably because of the Kakutani fixed point theorem, Kakutani is said to have replied, "What is the Kakutani fixed point theorem?"
(Comprehensive high-level mathematical treatment of fixed point theory, including the infinite dimensional analogues of Kakutani's theorem.)
(Standard reference on general equilibrium
theory. Chapter 5 uses Kakutani's theorem to prove the existence of equilibrium prices. Appendix C includes a proof of Kakutani's theorem and discusses its relationship with other mathematical results used in economics.)
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
, the Kakutani fixed-point theorem is a fixed-point theorem
Fixed-point theorem
In mathematics, a fixed-point theorem is a result saying that a function F will have at least one fixed point , under some conditions on F that can be stated in general terms...
for set-valued functions. It provides sufficient conditions for a set-valued function defined on a convex
Convex set
In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
, compact subset of a Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
to have a fixed point
Fixed point (mathematics)
In mathematics, a fixed point of a function is a point that is mapped to itself by the function. A set of fixed points is sometimes called a fixed set...
, i.e. a point which is map
Map (mathematics)
In most of mathematics and in some related technical fields, the term mapping, usually shortened to map, is either a synonym for function, or denotes a particular kind of function which is important in that branch, or denotes something conceptually similar to a function.In graph theory, a map is a...
ped to a set containing it. The Kakutani fixed point theorem is a generalization of Brouwer fixed point theorem
Brouwer fixed point theorem
Brouwer's fixed-point theorem is a fixed-point theorem in topology, named after Luitzen Brouwer. It states that for any continuous function f with certain properties there is a point x0 such that f = x0. The simplest form of Brouwer's theorem is for continuous functions f from a disk D to...
. The Brouwer fixed point theorem is a fundamental result in topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
which proves the existence of fixed points for continuous functions defined on compact, convex subsets of Euclidean spaces. Kakutani's theorem extends this to set-valued functions.
The theorem was developed by Shizuo Kakutani
Shizuo Kakutani
was a Japanese-born American mathematician, best known for his eponymous fixed-point theorem.Kakutani attended Tohoku University in Sendai, where his advisor was Tatsujirō Shimizu. Early in his career he spent two years at the Institute for Advanced Study in Princeton at the invitation of the...
in 1941 and was famously used by John Nash
John Nash
John Nash may refer to:*John Nash , Anglo-Welsh architect*John Forbes Nash, Jr. , American mathematician, 1994 Nobel Economics laureate, subject of the book and film titled A Beautiful Mind...
in his description of Nash equilibrium
Nash equilibrium
In game theory, Nash equilibrium is a solution concept of a game involving two or more players, in which each player is assumed to know the equilibrium strategies of the other players, and no player has anything to gain by changing only his own strategy unilaterally...
. It has subsequently found widespread application in game theory
Game theory
Game theory is a mathematical method for analyzing calculated circumstances, such as in games, where a person’s success is based upon the choices of others...
and economics
Economics
Economics is the social science that analyzes the production, distribution, and consumption of goods and services. The term economics comes from the Ancient Greek from + , hence "rules of the house"...
.
Statement
Kakutani's theorem states:- Let S be a non-emptyEmpty setIn mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
, compact and convexConvex setIn Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
subsetSubsetIn mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
of some Euclidean spaceEuclidean spaceIn mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
Rn. Let φ: S → 2S be a set-valued function on S with a closed graph and the property that φ(x) is non-empty and convex for all x ∈ S. Then φ has a fixed pointFixed point (mathematics)In mathematics, a fixed point of a function is a point that is mapped to itself by the function. A set of fixed points is sometimes called a fixed set...
.
When we say that the graph of
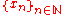is closed, we mean that for all sequences and 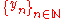such that , and 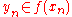for all , we have 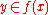.Definitions
Set-valued function: A set-valued function φ from the set X to the set Y is some rule that associates one or more points in Y with each point in X. Formally it can be seen just as an ordinary functionFunction (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
from X to the power set of Y, written as φ: X→2Y. Some prefer the term correspondence, which is used to refer to a function that for each input may return many outputs. Thus, each element of the domain corresponds to a subset of one or more elements of the range.
Closed graph: A set-valued function φ: X→2Y is said to have a closed graph if the set {(x,y)| y ∈ φ(x)} is a closed
Closed set
In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
subset of X×Y in the product topology
Product topology
In topology and related areas of mathematics, a product space is the cartesian product of a family of topological spaces equipped with a natural topology called the product topology...
.
Fixed point: Let φ: X→2X be a set-valued function. Then a ∈ X is a fixed point of φ if a ∈ φ(a).
Example
Interval (mathematics)
In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...
[0, 1] that maps a point x to the closed interval [1 − x/2, 1 − x/4]. Then f(x) satisfies all the assumptions of the theorem and must have fixed points.
In the diagram, any point on the 45° line (dotted line in red) which intersects the graph of the function (shaded in grey) is a fixed point, so in fact there is an infinity of fixed points in this particular case. For example, x = 0.72 (dashed line in blue) is a fixed point since 0.72 ∈ [1 − 0.72/2, 1 − 0.72/4].
Non-example
Consider the following function defined on [0,1]:
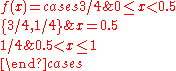
The function has no fixed point. Though it satisfies all other requirements of Kakutani's theorem, its value fails to be convex at x = 0.5.
Alternative statement
Some sources, including Kakutani's original paper, use the concept of upper hemicontinuity while stating the theorem:Empty set
In mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
, compact and convex
Convex set
In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
of some Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
Rn. Let φ: S→2S be an upper hemicontinuous set-valued function on S with the property that φ(x) is non-empty, closed
Closed set
In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
and convex for all x ∈ S. Then φ has a fixed point
Fixed point (mathematics)
In mathematics, a fixed point of a function is a point that is mapped to itself by the function. A set of fixed points is sometimes called a fixed set...
.
This statement of Kakutani's theorem is completely equivalent to the statement given at the beginning of this article.
We can show this by using the Closed graph theorem
Closed graph theorem
In mathematics, the closed graph theorem is a basic result in functional analysis which characterizes continuous linear operators between Banach spaces in terms of the operator graph.- The closed graph theorem :...
for set-valued functions, which says that a for a compact Hausdorff
Hausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
range space Y, a set-valued function φ: X→2Y has a closed graph if and only if it is upper hemicontinuous and φ(x) is a closed set for all x. Since all Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
s are Hausdorff (being metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
s) and φ is required to be closed-valued in the alternative statement of the Kakutani theorem, the Closed Graph Theorem implies that the two statements are equivalent.
Game theory
Mathematician John NashJohn Forbes Nash
John Forbes Nash, Jr. is an American mathematician whose works in game theory, differential geometry, and partial differential equations have provided insight into the forces that govern chance and events inside complex systems in daily life...
used the Kakutani fixed point theorem to prove a major result in game theory
Game theory
Game theory is a mathematical method for analyzing calculated circumstances, such as in games, where a person’s success is based upon the choices of others...
.
Stated informally, the theorem implies the existence of a Nash equilibrium
Nash equilibrium
In game theory, Nash equilibrium is a solution concept of a game involving two or more players, in which each player is assumed to know the equilibrium strategies of the other players, and no player has anything to gain by changing only his own strategy unilaterally...
in every finite game with mixed strategies for any number of players. This work would later earn him a Nobel Prize in Economics.
In this case, S is the set of tuple
Tuple
In mathematics and computer science, a tuple is an ordered list of elements. In set theory, an n-tuple is a sequence of n elements, where n is a positive integer. There is also one 0-tuple, an empty sequence. An n-tuple is defined inductively using the construction of an ordered pair...
s of mixed strategies chosen by each player in a game. The function φ(x) gives a new tuple where each player's strategy is her best response to other players' strategies in x. Since there may be a number of responses which are equally good, φ is set-valued rather than single-valued. Then the Nash equilibrium
Nash equilibrium
In game theory, Nash equilibrium is a solution concept of a game involving two or more players, in which each player is assumed to know the equilibrium strategies of the other players, and no player has anything to gain by changing only his own strategy unilaterally...
of the game is defined as a fixed point of φ, i.e. a tuple of strategies where each player's strategy is a best response to the strategies of the other players. Kakutani's theorem ensures that this fixed point exists.
General equilibrium
In general equilibriumGeneral equilibrium
General equilibrium theory is a branch of theoretical economics. It seeks to explain the behavior of supply, demand and prices in a whole economy with several or many interacting markets, by seeking to prove that a set of prices exists that will result in an overall equilibrium, hence general...
theory in economics, Kakutani's theorem has been used to prove the existence of set of prices which simultaneously equate supply with demand in all markets of an economy. The existence of such prices had been an open question in economics going back to at least Walras
Léon Walras
Marie-Esprit-Léon Walras was a French mathematical economist associated with the creation of the general equilibrium theory.-Life and career:...
. The first proof of this result was constructed by Lionel McKenzie.
In this case, S is the set of tuple
Tuple
In mathematics and computer science, a tuple is an ordered list of elements. In set theory, an n-tuple is a sequence of n elements, where n is a positive integer. There is also one 0-tuple, an empty sequence. An n-tuple is defined inductively using the construction of an ordered pair...
s of commodity prices. φ(x) is chosen as a function whose result is different from its arguments as long as the price-tuple x does not equate supply and demand everywhere. The challenge here is to construct φ so that it has this property while at the same time satisfying the conditions in Kakutani's theorem. If this can be done then φ has a fixed point according to the theorem. Given the way it was constructed, this fixed point must correspond to a price-tuple which equates supply with demand everywhere.
S = [0,1]
The proof of Kakutani's theorem is simplest for set-valued functions defined over closed intervalsInterval (mathematics)
In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...
of the real line. However, the proof of this case is instructive since its general strategy can be carried over to the higher dimensional case as well.
Let φ:
- Create a sequence of subdivisions of
[0,1] with adjacent points moving in opposite directions.
Let (ai, bi, pi, qi) for i = 0, 1, … be a sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
with the following properties:
| 1. | 1 ≥ bi > ai ≥ 0 | 2. | (bi − ai) ≤ 2−i |
| 3. | pi ∈ φ(ai) | 4. | qi ∈ φ(bi) |
| 5. | pi ≥ ai | 6. | qi ≤ bi |
Thus, the closed intervals
Such a sequence can be constructed as follows. Let a0 = 0 and b0 = 1. Let p0 be any point in φ(0) and q0 be any point in φ(1). Then, conditions (1)–(4) are immediately fulfilled. Moreover, since p0 ∈ φ(0) ⊂
Now suppose we have chosen ak, bk, pk and qk satisfying (1)–(6). Let,
- m = (ak+bk)/2.
Then m ∈
Convex set
In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
.
If there is a r ∈ φ(m) such that r ≥ m, then we take,
- ak+1 = m
- bk+1 = bk
- pk+1 = r
- qk+1 = qk
Otherwise, since φ(m) is non-empty, there must be a s ∈ φ(m) such that s ≤ m. In this case let,
- ak+1 = ak
- bk+1 = m
- pk+1 = pk
- qk+1 = s.
It can be verified that ak+1, bk+1, pk+1 and qk+1 satisfy conditions (1)–(6).
- Find a limiting point of the subdivisions.
The cartesian product
Cartesian product
In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
Tychonoff's theorem
In mathematics, Tychonoff's theorem states that the product of any collection of compact topological spaces is compact. The theorem is named after Andrey Nikolayevich Tychonoff, who proved it first in 1930 for powers of the closed unit interval and in 1935 stated the full theorem along with the...
. Since the sequence (an, pn, bn, qn) lies in this compact set, it must have a convergent
Limit of a sequence
The limit of a sequence is, intuitively, the unique number or point L such that the terms of the sequence become arbitrarily close to L for "large" values of n...
subsequence
Subsequence
In mathematics, a subsequence is a sequence that can be derived from another sequence by deleting some elements without changing the order of the remaining elements...
by the Bolzano-Weierstrass theorem. Let's fix attention on such a subsequence and let its limit be (a*, p*,b*,q*). Since the graph of φ is closed it must be the case that p* ∈ φ(a*) and q* ∈ φ(b*). Moreover, by condition (5), p* ≥ a* and by condition (6), q* ≤ b*.
But since (bi − ai) ≤ 2−i by condition (2),
- b* − a* = (lim bn) − (lim an) = lim (bn − an) = 0.
So, b* equals a*. Let x = b* = a*.
Then we have the situation that
- q* ∈ φ(x) ≤ x ≤ p* ∈ φ(x).
- Show that the limiting point is a fixed point.
If p* = q* then p* = x = q*. Since p* ∈ φ(x), x is a fixed point of φ.
Otherwise, since φ(x) is convex
Convex set
In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
and
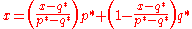
it once again follows that x must belong to φ(x) since p* and q* do and hence x is a fixed point of φ.
S is a n-simplex
In dimensions greater one, n-simplicesSimplex
In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...
are the simplest objects on which Kakutani's theorem can be proved. Informally, a n-simplex is the higher dimensional version of a triangle. Proving Kakutani's theorem for set-valued function defined on a simplex is not essentially different from proving it for intervals. The additional complexity in the higher-dimensional case exists in the first step of chopping up the domain into finer subpieces:
- Where we split intervals into two at the middle in the one-dimensional case, barycentric subdivisionBarycentric subdivisionIn geometry, the barycentric subdivision is a standard way of dividing an arbitrary convex polygon into triangles, a convex polyhedron into tetrahedra, or, in general, a convex polytope into simplices with the same dimension, by connecting the barycenters of their faces in a specific way.The name...
is used to break up a simplex into smaller sub-simplices. - While in the one-dimensional case we could use elementary arguments to pick one of the half-intervals in a way that its end-points were moved in opposite directions, in the case of simplices the combinatorialCombinatoricsCombinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
result known as Sperner's lemmaSperner's lemmaIn mathematics, Sperner's lemma is a combinatorial analog of the Brouwer fixed point theorem, which follows from it. Sperner's lemma states that every Sperner coloring of a triangulation of an n-dimensional simplex contains a cell colored with a complete set of colors...
is used to guarantee the existence of an appropriate subsimplex.
Once these changes have been made to the first step, the second and third steps of finding a limiting point and proving that it is a fixed point are almost unchanged from the one-dimensional case.
Arbitrary S
Kakutani's theorem for n-simplices can be used to prove the theorem for an arbitrary compact, convex S. Once again we employ the same technique of creating increasingly finer subdivisions. But instead of triangles with straight edges as in the case of n-simplices, we now use triangles with curved edges. In formal terms, we find a simplex which covers S and then move the problem from S to the simplex by using a deformation retractDeformation retract
In topology, a branch of mathematics, a retraction , as the name suggests, "retracts" an entire space into a subspace. A deformation retraction is a map which captures the idea of continuously shrinking a space into a subspace.- Retract :...
. Then we can apply the already established result for n-simplices.
Infinite dimensional generalizations
Kakutani's fixed point theorem was extended to infinite dimensional locally convex topological vector spaceLocally convex topological vector space
In functional analysis and related areas of mathematics, locally convex topological vector spaces or locally convex spaces are examples of topological vector spaces which generalize normed spaces. They can be defined as topological vector spaces whose topology is generated by translations of ...
s by Irving Glicksberg
and Ky Fan
Ky Fan
Ky Fan was an American mathematician and Emeritus Professor of Mathematics at the University of California, Santa Barbara .-Biography:...
.
To state the theorem in this case, we need a few more definitions:
Upper semicontinuity: A set-valued function φ: X→2Y is upper semicontinuous if for every open set
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
W ⊂ Y, the set {x| φ(x) ⊂ W} is open in X.
Kakutani map: Let X and Y be topological vector space
Topological vector space
In mathematics, a topological vector space is one of the basic structures investigated in functional analysis...
s and φ: X→2Y be a set-valued function. If Y is convex, then φ is termed a Kakutani map if it is upper semicontinuous and φ(x) is non-empty, compact and convex for all x ∈ X.
Then the Kakutani-Glicksberg-Fan theorem can be stated as:
- Let S be a non-emptyEmpty setIn mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
, compact and convexConvex setIn Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
subsetSubsetIn mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
of a locally convex topological vector spaceLocally convex topological vector spaceIn functional analysis and related areas of mathematics, locally convex topological vector spaces or locally convex spaces are examples of topological vector spaces which generalize normed spaces. They can be defined as topological vector spaces whose topology is generated by translations of ...
. Let φ: S→2S be a Kakutani map. Then φ has a fixed point.
The corresponding result for single-valued functions is the Tychonoff fixed point theorem.
If the space on which the function is defined is Hausdorff
Hausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
in addition to being locally convex, then the statement of the theorem becomes the same as that in the Euclidean
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
case:
- Let S be a non-emptyEmpty setIn mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
, compact and convexConvex setIn Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
subsetSubsetIn mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
of a locally convexLocally convex topological vector spaceIn functional analysis and related areas of mathematics, locally convex topological vector spaces or locally convex spaces are examples of topological vector spaces which generalize normed spaces. They can be defined as topological vector spaces whose topology is generated by translations of ...
Hausdorff spaceHausdorff spaceIn topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
. Let φ: S→2S be a set-valued function on S which has a closed graph and the property that φ(x) is non-empty and convex for all x ∈ S. Then the set of fixed pointsFixed point (mathematics)In mathematics, a fixed point of a function is a point that is mapped to itself by the function. A set of fixed points is sometimes called a fixed set...
of φ is non-empty and compact.
Anecdote
In his game theory textbook,Ken Binmore recalls that Kakutani once asked him at a conference why so many economists had attended his talk. When Binmore told him that it was probably because of the Kakutani fixed point theorem, Kakutani is said to have replied, "What is the Kakutani fixed point theorem?"
Further reading
(Standard reference on fixed-point theory for economists. Includes a proof of Kakutani's theorem.)(Comprehensive high-level mathematical treatment of fixed point theory, including the infinite dimensional analogues of Kakutani's theorem.)
(Standard reference on general equilibrium
General equilibrium
General equilibrium theory is a branch of theoretical economics. It seeks to explain the behavior of supply, demand and prices in a whole economy with several or many interacting markets, by seeking to prove that a set of prices exists that will result in an overall equilibrium, hence general...
theory. Chapter 5 uses Kakutani's theorem to prove the existence of equilibrium prices. Appendix C includes a proof of Kakutani's theorem and discusses its relationship with other mathematical results used in economics.)
External links
- Fixed Point Theorems. (Page on fixed point theorems from the New SchoolThe New SchoolThe New School is a university in New York City, located mostly in Greenwich Village. From its founding in 1919 by progressive New York academics, and for most of its history, the university was known as the New School for Social Research. Between 1997 and 2005 it was known as New School University...
's History of Economic Thought site.)