
Convex set
Encyclopedia


Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object. For example, a solid cube is convex, but anything that is hollow or has a dent in it, for example, a crescent
Crescent
In art and symbolism, a crescent is generally the shape produced when a circular disk has a segment of another circle removed from its edge, so that what remains is a shape enclosed by two circular arcs of different diameters which intersect at two points .In astronomy, a crescent...
shape, is not convex.
The notion can be generalized to other spaces as described below.
In vector spaces

Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
over the real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s, or, more generally, some ordered field
Ordered field
In mathematics, an ordered field is a field together with a total ordering of its elements that is compatible with the field operations. Historically, the axiomatization of an ordered field was abstracted gradually from the real numbers, by mathematicians including David Hilbert, Otto Hölder and...
. This includes Euclidean spaces. A set C in S is said to be convex if, for all x and y in C and all t in the interval
Interval (mathematics)
In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...
[0,1], the point
x + t y
is in C. In other words, every point on the line segment
Line segment
In geometry, a line segment is a part of a line that is bounded by two end points, and contains every point on the line between its end points. Examples of line segments include the sides of a triangle or square. More generally, when the end points are both vertices of a polygon, the line segment...
connecting x and y is in C. This implies that a convex set in a real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
or complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
topological vector space
Topological vector space
In mathematics, a topological vector space is one of the basic structures investigated in functional analysis...
is path-connected, thus connected
Connected space
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
.
A set C is called absolutely convex if it is convex and balanced
Balanced set
In linear algebra and related areas of mathematics a balanced set, circled set or disk in a vector space is a set S so that for all scalars α with |α| ≤ 1\alpha S \subseteq S...
.
The convex subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
s of R (the set of real numbers) are simply the intervals of R.
Some examples of convex subsets of Euclidean 2-space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
are regular polygon
Regular polygon
A regular polygon is a polygon that is equiangular and equilateral . Regular polygons may be convex or star.-General properties:...
s and bodies of constant width
Curve of constant width
In geometry, a curve of constant width is a convex planar shape whose width, defined as the perpendicular distance between two distinct parallel lines each intersecting its boundary in a single point, is the same regardless of the direction of those two parallel lines.More generally, any compact...
.
Some examples of convex subsets of Euclidean 3-space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
are the Archimedean solid
Archimedean solid
In geometry an Archimedean solid is a highly symmetric, semi-regular convex polyhedron composed of two or more types of regular polygons meeting in identical vertices...
s and the Platonic solid
Platonic solid
In geometry, a Platonic solid is a convex polyhedron that is regular, in the sense of a regular polygon. Specifically, the faces of a Platonic solid are congruent regular polygons, with the same number of faces meeting at each vertex; thus, all its edges are congruent, as are its vertices and...
s. The Kepler-Poinsot polyhedra are examples of non-convex sets.
Properties
If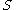 is a convex set, for any
is a convex set, for any 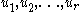 in
in  , and any nonnegative numbers
, and any nonnegative numbers  such that
such that  , then the vector
, then the vector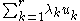
is in
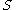 . A vector of this type is known as a convex combination
. A vector of this type is known as a convex combinationConvex combination
In convex geometry, a convex combination is a linear combination of points where all coefficients are non-negative and sum up to 1....
of
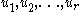 .
.Intersections and unions
The collection of convex subsets of a vector space has the following properties:- The empty setEmpty setIn mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
and the whole vector-space are convex. - The intersection of any collection of convex sets is convex.
- The union of a non-decreasing sequenceNet (mathematics)In mathematics, more specifically in general topology and related branches, a net or Moore–Smith sequence is a generalization of the notion of a sequence. In essence, a sequence is a function with domain the natural numbers, and in the context of topology, the range of this function is...
of convex subsets is a convex set.
For the preceding property of unions of non-decreasing sequences of convex sets, the restriction to nested sets was important: The union of two convex sets need not be convex.
Convex hulls
Every subset A of the vector space is contained within a smallest convex set (called the convex hullConvex hull
In mathematics, the convex hull or convex envelope for a set of points X in a real vector space V is the minimal convex set containing X....
of A), namely the intersection of all convex sets containing A.
The convex-hull operator Conv has the characteristic properties of a hull operator
Closure operator
In mathematics, a closure operator on a set S is a function cl: P → P from the power set of S to itself which satisfies the following conditions for all sets X,Y ⊆ S....
:
| extensive | S ⊆ Conv(S), |
| non-decreasing | S ⊆ T implies that Conv(S) ⊆ Conv(T), and |
| idempotent Idempotence Idempotence is the property of certain operations in mathematics and computer science, that they can be applied multiple times without changing the result beyond the initial application... |
Conv(Conv(S)) = Conv(S). |
The convex-hull operation is needed for the set of convex sets to form a lattice
Lattice (order)
In mathematics, a lattice is a partially ordered set in which any two elements have a unique supremum and an infimum . Lattices can also be characterized as algebraic structures satisfying certain axiomatic identities...
, in which the "join" operation
Join and meet
In mathematics, join and meet are dual binary operations on the elements of a partially ordered set. A join on a set is defined as the supremum with respect to a partial order on the set, provided a supremum exists...
is the convex hull of the union of two convex sets
- Conv(S)∨Conv(T) = Conv( S ∪ T ) = Conv( Conv(S) ∪ Conv(T) ).
The intersection of any collection of convex sets is itself convex, so the convex subsets of a (real or complex) vector space form a complete lattice
Lattice (order)
In mathematics, a lattice is a partially ordered set in which any two elements have a unique supremum and an infimum . Lattices can also be characterized as algebraic structures satisfying certain axiomatic identities...
.
Minkowski addition
- In a real vector-space, the Minkowski sumMinkowski additionIn geometry, the Minkowski sum of two sets A and B in Euclidean space is the result of adding every element of A to every element of B, i.e...
of two (non-empty) sets S1 and S2 is defined to be the setSumsetIn additive combinatorics, the sumset of two subsets A and B of an abelian group G is defined to be the set of all sums of an element from A with an element from B...
S1 + S2 formed by the addition of vectors element-wise from the summand-sets
- S1 + S2 = { x1 + x2 : x1 ∈ S1 and x2 ∈ S2 }.
More generally, the Minkowski sum of a finite family of (non-empty) sets Sn is the set formed by element-wise addition of vectors
- ∑ Sn = { ∑ xn : xn ∈ Sn }.
For Minkowski addition, the zero set {0} containing only the zero vector
Null vector
Null vector can refer to:* Null vector * A causal structure in Minkowski space...
0 has special importance
Identity element
In mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...
: For every non-empty subset S of a vector space
- S + {0} = S;
in algebraic terminology, the zero vector 0 is the identity element
Identity element
In mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...
of Minkowski addition (on the collection of non-empty sets).
Convex hulls of Minkowski sums
Minkowski addition behaves well with respect to the operation of taking convex hulls, as shown by the following proposition:- For all subsets S1 and S2 of a real vector-space, the convex hullConvex hullIn mathematics, the convex hull or convex envelope for a set of points X in a real vector space V is the minimal convex set containing X....
of their Minkowski sum is the Minkowski sum of their convex hulls
- Conv( S1 + S2 ) = Conv( S1 ) + Conv( S2 ).
This result holds more generally for each finite collection of non-empty sets
- Conv( ∑ Sn ) = ∑ Conv( Sn ).
In mathematical terminology, the operation
Operation (mathematics)
The general operation as explained on this page should not be confused with the more specific operators on vector spaces. For a notion in elementary mathematics, see arithmetic operation....
s of Minkowski summation and of forming convex hull
Convex hull
In mathematics, the convex hull or convex envelope for a set of points X in a real vector space V is the minimal convex set containing X....
s are commuting
Commutativity
In mathematics an operation is commutative if changing the order of the operands does not change the end result. It is a fundamental property of many binary operations, and many mathematical proofs depend on it...
operations.
Closed convex sets
ClosedClosed set
In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
convex sets can be characterised as the intersections of closed half-space
Half-space
In geometry, a half-space is either of the two parts into which a plane divides the three-dimensional euclidean space. More generally, a half-space is either of the two parts into which a hyperplane divides an affine space...
s (sets of point in space that lie on and to one side of a hyperplane
Hyperplane
A hyperplane is a concept in geometry. It is a generalization of the plane into a different number of dimensions.A hyperplane of an n-dimensional space is a flat subset with dimension n − 1...
). From what has just been said, it is clear that such intersections are convex, and they will also be closed sets. To prove the converse, i.e., every convex set may be represented as such intersection, one needs the supporting hyperplane theorem in the form that for a given closed convex set C and point P outside it, there is a closed half-space H that contains C and not P. The supporting hyperplane theorem is a special case of the Hahn–Banach theorem
Hahn–Banach theorem
In mathematics, the Hahn–Banach theorem is a central tool in functional analysis. It allows the extension of bounded linear functionals defined on a subspace of some vector space to the whole space, and it also shows that there are "enough" continuous linear functionals defined on every normed...
of functional analysis
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
.
The Minkowski sum of two compact convex sets is closed, as is the sum of a compact convex set and a closed convex set.
Generalizations and extensions for convexity
The notion of convexity in the Euclidean space may be generalized by modifying the definition in some or other aspects. The common name "generalized convexity" is used, because the resulting objects retain certain properties of convex sets.Star-convex sets
Let C be a set in a real or complex vector space. C is star convex if there exists an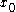 in C such that the line segment from
in C such that the line segment from 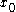 to any point y in C is contained in C. Hence a non-empty convex set is always star-convex but a star-convex set is not always convex.
to any point y in C is contained in C. Hence a non-empty convex set is always star-convex but a star-convex set is not always convex.Orthogonal convexity
An example of generalized convexity is orthogonal convexity.A set S in the Euclidean space is called orthogonally convex or ortho-convex, if any segment parallel to any of the coordinate axes connecting two points of S lies totally within S. It is easy to prove that an intersection of any collection of orthoconvex sets is orthoconvex. Some other properties of convex sets are valid as well.
Not Euclidean geometry
The definition of a convex set and a convex hull extends naturally to geometries which are not Euclidean by defining a geodesically convex setGeodesic convexity
In mathematics — specifically, in Riemannian geometry — geodesic convexity is a natural generalization of convexity for sets and functions to Riemannian manifolds...
to be one that contains the geodesic
Geodesic
In mathematics, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a Riemannian metric, geodesics are defined to be the shortest path between points in the space...
s joining any two points in the set.
Order topology
Convexity can be extended for a space endowed with the order topology
endowed with the order topologyOrder topology
In mathematics, an order topology is a certain topology that can be defined on any totally ordered set. It is a natural generalization of the topology of the real numbers to arbitrary totally ordered sets...
, using the total order
Total order
In set theory, a total order, linear order, simple order, or ordering is a binary relation on some set X. The relation is transitive, antisymmetric, and total...
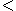 of the space.
of the space.Let
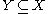 . The subspace
. The subspace 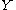 is a convex set if for each pair of points
is a convex set if for each pair of points 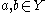 such that
such that  , the interval
, the interval 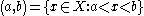 is contained in
is contained in 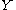 . That is,
. That is, 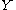 is convex if and only if
is convex if and only if 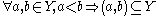 .
.Convexity spaces
The notion of convexity may be generalised to other objects, if certain properties of convexity are selected as axiomAxiom
In traditional logic, an axiom or postulate is a proposition that is not proven or demonstrated but considered either to be self-evident or to define and delimit the realm of analysis. In other words, an axiom is a logical statement that is assumed to be true...
s.
Given a set X, a convexity over X is a collection
 of subsets of X satisfying the following axioms:
of subsets of X satisfying the following axioms:- The empty set and X are in
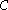
- The intersection of any collection from
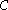 is in
is in  .
. - The union of a chainTotal orderIn set theory, a total order, linear order, simple order, or ordering is a binary relation on some set X. The relation is transitive, antisymmetric, and total...
(with respect to the inclusion relation) of elements of is in
is in 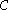 .
.
The elements of
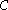 are called convex sets and the pair (X,
are called convex sets and the pair (X,  ) is called a convexity space. For the ordinary convexity, the first two axioms hold, and the third one is trivial.
) is called a convexity space. For the ordinary convexity, the first two axioms hold, and the third one is trivial.For an alternative definition of abstract convexity, more suited to discrete geometry
Discrete geometry
Discrete geometry and combinatorial geometry are branches of geometry that study combinatorial properties and constructive methods of discrete geometric objects. Most questions in discrete geometry involve finite or discrete sets of basic geometric objects, such as points, lines, planes, circles,...
, see the convex geometries associated with antimatroid
Antimatroid
In mathematics, an antimatroid is a formal system that describes processes in which a set is built up by including elements one at a time, and in which an element, once available for inclusion, remains available until it is included...
s.
See also
- Convex functionConvex functionIn mathematics, a real-valued function f defined on an interval is called convex if the graph of the function lies below the line segment joining any two points of the graph. Equivalently, a function is convex if its epigraph is a convex set...
- Holomorphically convex hullHolomorphically convex hullIn mathematics, more precisely in complex analysis, the holomorphically convex hull of a given compact set in the n-dimensional complex space Cn is defined as follows....
- Pseudoconvexity
- Convex metric spaceConvex metric spaceIn mathematics, convex metric spaces are, intuitively, metric spaces with the property any "segment" joining two points in that space has other points in it besides the endpoints....
- Concave setConcave setIn mathematics, the notion of a "concave set" is not correct. A set that is not convex, is a non-convex set....
- Helly's theoremHelly's theoremHelly's theorem is a basic result in discrete geometry describing the ways that convex sets may intersect each other. It was discovered by Eduard Helly in 1913, but not published by him until 1923, by which time alternative proofs by and had already appeared...
- Carathéodory's theorem (convex hull)Carathéodory's theorem (convex hull)In convex geometry Carathéodory's theorem states that if a point x of Rd lies in the convex hull of a set P, there is a subset P′ of P consisting of d+1 or fewer points such that x lies in the convex hull of P′. Equivalently, x lies in an r-simplex with vertices in P, where r \leq d...
- Choquet theoryChoquet theoryIn mathematics, Choquet theory is an area of functional analysis and convex analysis created by Gustave Choquet. It is concerned with measures with support on the extreme points of a convex set C...
- Shapley–Folkman lemmaShapley–Folkman lemmaIn geometry and economics, the Shapley–Folkman lemma describes the Minkowski addition of sets in a vector space. Minkowski addition is defined as the addition of the sets' members: for example, adding the set consisting of the integers zero and one to itself yields the set consisting of...
External links
- Lectures on Convex Sets, notes by Niels Lauritzen, at Aarhus University, March 2010.

