Order topology
Encyclopedia
In mathematics
, an order topology is a certain topology
that can be defined on any totally ordered set. It is a natural generalization of the topology of the real numbers to arbitrary totally ordered sets.
If X is a totally ordered set, the order topology on X is generated by the subbase
of "open rays"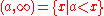
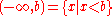
for all a,b in X. This is equivalent to saying that the open interval
s
together with the above rays form a base
for the order topology. The open sets in X are the sets that are a union
of (possibly infinitely many) such open intervals and rays.
The order topology makes X into a completely normal Hausdorff space
.
The standard topologies on R, Q, and N are the order topologies.
. The subspace topology is always at least as fine as the induced order topology, but they are not in general the same.
For example, consider the subset Y = {–1} ∪ {1/n}n∈N in the rationals. Under the subspace topology, the singleton set {–1} is open in Y, but under the induced order topology, any open set containing –1 must contain all but finitely many members of the space.
We wish to define here a subset Z of a linearly ordered topological space X such that no total order on Z generates the subspace topology on Z, so that the subspace topology will not be an order topology even though it is the subspace topology of a space whose topology is an order topology.
Let
in the real line. The same argument as before shows that the subspace topology on Z is not equal to the induced order topology on Z, but one can show that the subspace topology on Z cannot be equal to any order topology on Z.
An argument follows. Suppose by way of contradiction that there is some strict total order < = <1 on Z such that the order topology generated by < is equal to the subspace topology on Z (note that we are not assuming that < is the induced order on Z, but rather an arbitrarily given total order on Z that generates the subspace topology). In the following, interval notation should be interpreted relative to the < relation. Also, if A and B are sets, A
Let M=Z\{-1}, the unit interval. M is connected. If m,n∈M and m<-1 A. Then (-1,a)=[p,a), so [p,a) is open. {p}∪A=[p,a)∪A, so {p}∪A is an open subset of M and hence M = ({p}∪A) ∪ B is the union of two disjoint open subsets of M so M is not connected, a contradiction.
A space whose topology is an order topology is called a Linearly Ordered Topological Space (LOTS), and a subspace of a linearly ordered topological space is called a Generalized Ordered Space (GO-space). Thus the example Z above is an example of a GO-space that is not a linearly ordered topological space.
The left and right order topologies can be used to give counterexamples in general topology. For example, the left or right order topology on a bounded set provides an example of a compact space
that is not Hausdorff.
The left order topology is the standard topology used for many set-theoretic purposes on a Boolean algebra.
λ one can consider the spaces of ordinal numbers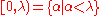
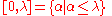
together with the natural order topology. These spaces are called ordinal spaces. (Note that in the usual set-theoretic construction of ordinal numbers we have λ = [0,λ) and λ + 1 = [0,λ]). Obviously, these spaces are mostly of interest when λ is an infinite ordinal; otherwise (for finite ordinals), the order topology is simply the discrete topology.
When λ = ω (the first infinite ordinal), the space [0,ω) is just N with the usual (still discrete) topology, while [0,ω] is the one-point compactification of N.
Of particular interest is the case when λ = ω1, the set of all countable ordinals, and the first uncountable ordinal
. The element ω1 is a limit point
of the subset [0,ω1) even though no sequence of elements in [0,ω1) has the element ω1 as its limit. In particular, [0,ω1] is not first-countable
. The subspace [0,ω1) is first-countable however, since the only point without a countable local base is ω1. Some further properties include
can be made into a topological space
by endowing it with the order topology (since, being well-ordered, an ordinal is in particular totally ordered
): in the absence of indication to the contrary, it is always that order topology which is meant when an ordinal is thought of as a topological space. (Note that if we are willing to accept a proper class as a topological space, then the class of all ordinals is also a topological space for the order topology.)
The set of limit point
s of an ordinal α is precisely the set of limit ordinals less than α. Successor ordinals (and zero) less than α are isolated point
s in α. In particular, the finite ordinals and ω are discrete
topological spaces, and no ordinal beyond that is discrete. The ordinal α is compact
as a topological space if and only if α is a successor ordinal
.
The closed sets of a limit ordinal α are just the closed sets in the sense that we have already defined, namely, those which contain a limit ordinal whenever they contain all sufficiently large ordinals below it.
Any ordinal is, of course, an open subset of any further ordinal. We can also define the topology on the ordinals in the following inductive way: 0 is the empty topological space, α+1 is obtained by taking the one-point compactification
of α (if α is a limit ordinal; if it is not, α+1 is merely the disjoint union of α and a point), and for δ a limit ordinal, δ is equipped with the inductive limit
topology.
As topological spaces, all the ordinals are Hausdorff
and even normal
. They are also totally disconnected
(connected components are points), scattered (every non-empty set has an isolated point; in this case, just take the smallest element), zero-dimensional
(the topology has a clopen basis: here, write an open interval (β,γ) as the union of the clopen intervals (β,γ'+1)=[ β+1,γ'] for γ'<γ). However, they are not extremally disconnected
in general (there is an open set, namely ω, whose closure is not open).
The topological spaces ω1 and its successor ω1+1 are frequently used as text-book examples of non-countable topological spaces.
For example, in the topological space ω1+1, the element ω1 is in the closure of the subset ω1 even though no sequence of elements in ω1 has the element ω1 as its limit: an element in ω1 is a countable set; for any sequence of such sets, the union of these sets is the union of countably many countable sets, so still countable; this union is an upper bound of the elements of the sequence, and therefore of the limit of the sequence, if it has one.
The space ω1 is first-countable
, but not second-countable
, and ω1+1 has neither of these two properties, despite being compact
. It is also worthy of note that any continuous function from ω1 to R (the real line
) is eventually constant: so the Stone-Čech compactification
of ω1 is ω1+1, just as its one-point compactification (in sharp contrast to ω, whose Stone-Čech compactification is much larger than ω).
. An ordinary sequence corresponds to the case α = ω.
If X is a topological space, we say that an α-indexed sequence of elements of X converges to a limit x when it converges as a net
, in other words, when given any neighborhood U of x there is an ordinal β<α such that xι is in U for all ι≥β.
Ordinal-indexed sequences are more powerful than ordinary (ω-indexed) sequences to determine limits in topology: for example, ω1 (omega-one, the set of all countable ordinal numbers, and the smallest uncountable ordinal number), is a limit point of ω1+1 (because it is a limit ordinal), and, indeed, it is the limit of the ω1-indexed sequence which maps any ordinal less than ω1 to itself: however, it is not the limit of any ordinary (ω-indexed) sequence in ω1, since any such limit is less than or equal to the union of its elements, which is a countable union of countable sets, hence itself countable.
However, ordinal-indexed sequences are not powerful enough to replace nets (or filters
) in general: for example, on the Tychonoff plank
(the product space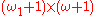
), the corner point 
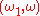is a limit point (it is in the closure) of the open subset 
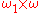, but it is not the limit of an ordinal-indexed sequence.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, an order topology is a certain topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
that can be defined on any totally ordered set. It is a natural generalization of the topology of the real numbers to arbitrary totally ordered sets.
If X is a totally ordered set, the order topology on X is generated by the subbase
Subbase
In topology, a subbase for a topological space X with topology T is a subcollection B of T which generates T, in the sense that T is the smallest topology containing B...
of "open rays"
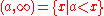
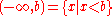
for all a,b in X. This is equivalent to saying that the open interval
Interval (mathematics)
In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...
s
together with the above rays form a base
Base (topology)
In mathematics, a base B for a topological space X with topology T is a collection of open sets in T such that every open set in T can be written as a union of elements of B. We say that the base generates the topology T...
for the order topology. The open sets in X are the sets that are a union
Union (set theory)
In set theory, the union of a collection of sets is the set of all distinct elements in the collection. The union of a collection of sets S_1, S_2, S_3, \dots , S_n\,\! gives a set S_1 \cup S_2 \cup S_3 \cup \dots \cup S_n.- Definition :...
of (possibly infinitely many) such open intervals and rays.
The order topology makes X into a completely normal Hausdorff space
Hausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
.
The standard topologies on R, Q, and N are the order topologies.
Induced order topology
If Y is a subset of X, then Y inherits a total order from X. Y therefore has an order topology, the induced order topology. As a subset of X, Y also has a subspace topologySubspace topology
In topology and related areas of mathematics, a subspace of a topological space X is a subset S of X which is equipped with a natural topology induced from that of X called the subspace topology .- Definition :Given a topological space and a subset S of X, the...
. The subspace topology is always at least as fine as the induced order topology, but they are not in general the same.
For example, consider the subset Y = {–1} ∪ {1/n}n∈N in the rationals. Under the subspace topology, the singleton set {–1} is open in Y, but under the induced order topology, any open set containing –1 must contain all but finitely many members of the space.
An example of a subspace of a linearly ordered space whose topology is not an order topology
Though the subspace topology of Y = {–1} ∪ {1/n}n∈N in the section above is shown to be not generated by the induced order on Y, it is nonetheless an order topology on Y; indeed, in the subspace topology every point is isolated (i.e., singleton {y} is open in Y for every y in Y), so the subspace topology is the discrete topology on Y (the topology in which every subset of Y is an open set), and the discrete topology on any set is an order topology. To define a total order on Y that generates the discrete topology on Y, simply modify the induced order on Y by defining -1 to be the greatest element of Y and otherwise keeping the same order for the other points, so that in this new order (call it say <1) we have 1/n <1 –1 for all n∈N. Then, in the order topology on Y generated by <1, every point of Y is isolated in Y.We wish to define here a subset Z of a linearly ordered topological space X such that no total order on Z generates the subspace topology on Z, so that the subspace topology will not be an order topology even though it is the subspace topology of a space whose topology is an order topology.
Let
in the real line. The same argument as before shows that the subspace topology on Z is not equal to the induced order topology on Z, but one can show that the subspace topology on Z cannot be equal to any order topology on Z.An argument follows. Suppose by way of contradiction that there is some strict total order < = <1 on Z such that the order topology generated by < is equal to the subspace topology on Z (note that we are not assuming that < is the induced order on Z, but rather an arbitrarily given total order on Z that generates the subspace topology). In the following, interval notation should be interpreted relative to the < relation. Also, if A and B are sets, A
Let M=Z\{-1}, the unit interval. M is connected. If m,n∈M and m<-1
A space whose topology is an order topology is called a Linearly Ordered Topological Space (LOTS), and a subspace of a linearly ordered topological space is called a Generalized Ordered Space (GO-space). Thus the example Z above is an example of a GO-space that is not a linearly ordered topological space.
Left and right order topologies
Several variants of the order topology can be given:- The right order topology on X is the topology whose open sets consist of intervals of the form (a, ∞).
- The left order topology on X is the topology whose open sets consist of intervals of the form (−∞, b).
The left and right order topologies can be used to give counterexamples in general topology. For example, the left or right order topology on a bounded set provides an example of a compact space
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
that is not Hausdorff.
The left order topology is the standard topology used for many set-theoretic purposes on a Boolean algebra.
Ordinal space
For any ordinal numberOrdinal number
In set theory, an ordinal number, or just ordinal, is the order type of a well-ordered set. They are usually identified with hereditarily transitive sets. Ordinals are an extension of the natural numbers different from integers and from cardinals...
λ one can consider the spaces of ordinal numbers
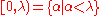
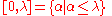
together with the natural order topology. These spaces are called ordinal spaces. (Note that in the usual set-theoretic construction of ordinal numbers we have λ = [0,λ) and λ + 1 = [0,λ]). Obviously, these spaces are mostly of interest when λ is an infinite ordinal; otherwise (for finite ordinals), the order topology is simply the discrete topology.
When λ = ω (the first infinite ordinal), the space [0,ω) is just N with the usual (still discrete) topology, while [0,ω] is the one-point compactification of N.
Of particular interest is the case when λ = ω1, the set of all countable ordinals, and the first uncountable ordinal
First uncountable ordinal
In mathematics, the first uncountable ordinal, traditionally denoted by ω1 or sometimes by Ω, is the smallest ordinal number that, considered as a set, is uncountable. It is the supremum of all countable ordinals...
. The element ω1 is a limit point
Limit point
In mathematics, a limit point of a set S in a topological space X is a point x in X that can be "approximated" by points of S in the sense that every neighbourhood of x with respect to the topology on X also contains a point of S other than x itself. Note that x does not have to be an element of S...
of the subset [0,ω1) even though no sequence of elements in [0,ω1) has the element ω1 as its limit. In particular, [0,ω1] is not first-countable
First-countable space
In topology, a branch of mathematics, a first-countable space is a topological space satisfying the "first axiom of countability". Specifically, a space X is said to be first-countable if each point has a countable neighbourhood basis...
. The subspace [0,ω1) is first-countable however, since the only point without a countable local base is ω1. Some further properties include
- neither [0,ω1) or [0,ω1] is separable or second-countable
- [0,ω1] is compactCompact spaceIn mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
while [0,ω1) is sequentially compactSequentially compact spaceIn mathematics, a topological space is sequentially compact if every sequence has a convergent subsequence. For general topological spaces, the notions of compactness and sequential compactness are not equivalent; they are, however, equivalent for metric spaces....
and countably compactCountably compact spaceIn mathematics a topological space is countably compact if every countable open cover has a finite subcover.-Examples and Properties:A compact space is countably compact...
, but not compact or paracompact
Ordinals as topological spaces
Any ordinal numberOrdinal number
In set theory, an ordinal number, or just ordinal, is the order type of a well-ordered set. They are usually identified with hereditarily transitive sets. Ordinals are an extension of the natural numbers different from integers and from cardinals...
can be made into a topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
by endowing it with the order topology (since, being well-ordered, an ordinal is in particular totally ordered
Total order
In set theory, a total order, linear order, simple order, or ordering is a binary relation on some set X. The relation is transitive, antisymmetric, and total...
): in the absence of indication to the contrary, it is always that order topology which is meant when an ordinal is thought of as a topological space. (Note that if we are willing to accept a proper class as a topological space, then the class of all ordinals is also a topological space for the order topology.)
The set of limit point
Limit point
In mathematics, a limit point of a set S in a topological space X is a point x in X that can be "approximated" by points of S in the sense that every neighbourhood of x with respect to the topology on X also contains a point of S other than x itself. Note that x does not have to be an element of S...
s of an ordinal α is precisely the set of limit ordinals less than α. Successor ordinals (and zero) less than α are isolated point
Isolated point
In topology, a branch of mathematics, a point x of a set S is called an isolated point of S, if there exists a neighborhood of x not containing other points of S.In particular, in a Euclidean space ,...
s in α. In particular, the finite ordinals and ω are discrete
Discrete space
In topology, a discrete space is a particularly simple example of a topological space or similar structure, one in which the points are "isolated" from each other in a certain sense.- Definitions :Given a set X:...
topological spaces, and no ordinal beyond that is discrete. The ordinal α is compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
as a topological space if and only if α is a successor ordinal
Successor ordinal
In set theory, the successor of an ordinal number α is the smallest ordinal number greater than α. An ordinal number that is a successor is called a successor ordinal...
.
The closed sets of a limit ordinal α are just the closed sets in the sense that we have already defined, namely, those which contain a limit ordinal whenever they contain all sufficiently large ordinals below it.
Any ordinal is, of course, an open subset of any further ordinal. We can also define the topology on the ordinals in the following inductive way: 0 is the empty topological space, α+1 is obtained by taking the one-point compactification
Compactification (mathematics)
In mathematics, compactification is the process or result of making a topological space compact. The methods of compactification are various, but each is a way of controlling points from "going off to infinity" by in some way adding "points at infinity" or preventing such an "escape".-An...
of α (if α is a limit ordinal; if it is not, α+1 is merely the disjoint union of α and a point), and for δ a limit ordinal, δ is equipped with the inductive limit
Direct limit
In mathematics, a direct limit is a colimit of a "directed family of objects". We will first give the definition for algebraic structures like groups and modules, and then the general definition which can be used in any category.- Algebraic objects :In this section objects are understood to be...
topology.
As topological spaces, all the ordinals are Hausdorff
Hausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
and even normal
Normal space
In topology and related branches of mathematics, a normal space is a topological space X that satisfies Axiom T4: every two disjoint closed sets of X have disjoint open neighborhoods. A normal Hausdorff space is also called a T4 space...
. They are also totally disconnected
Totally disconnected space
In topology and related branches of mathematics, a totally disconnected space is a topological space that is maximally disconnected, in the sense that it has no non-trivial connected subsets...
(connected components are points), scattered (every non-empty set has an isolated point; in this case, just take the smallest element), zero-dimensional
Zero-dimensional space
In mathematics, a zero-dimensional topological space is a topological space that has dimension zero with respect to one of several inequivalent notions of assigning a dimension to a given topological space...
(the topology has a clopen basis: here, write an open interval (β,γ) as the union of the clopen intervals (β,γ'+1)=
Extremally disconnected space
In mathematics, a topological space is termed extremally disconnected or extremely disconnected if the closure of every open set in it is open. An extremally disconnected space that is also compact and Hausdorff is sometimes called a Stonean space...
in general (there is an open set, namely ω, whose closure is not open).
The topological spaces ω1 and its successor ω1+1 are frequently used as text-book examples of non-countable topological spaces.
For example, in the topological space ω1+1, the element ω1 is in the closure of the subset ω1 even though no sequence of elements in ω1 has the element ω1 as its limit: an element in ω1 is a countable set; for any sequence of such sets, the union of these sets is the union of countably many countable sets, so still countable; this union is an upper bound of the elements of the sequence, and therefore of the limit of the sequence, if it has one.
The space ω1 is first-countable
First-countable space
In topology, a branch of mathematics, a first-countable space is a topological space satisfying the "first axiom of countability". Specifically, a space X is said to be first-countable if each point has a countable neighbourhood basis...
, but not second-countable
Second-countable space
In topology, a second-countable space, also called a completely separable space, is a topological space satisfying the second axiom of countability. A space is said to be second-countable if its topology has a countable base...
, and ω1+1 has neither of these two properties, despite being compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
. It is also worthy of note that any continuous function from ω1 to R (the real line
Real line
In mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one...
) is eventually constant: so the Stone-Čech compactification
Compactification (mathematics)
In mathematics, compactification is the process or result of making a topological space compact. The methods of compactification are various, but each is a way of controlling points from "going off to infinity" by in some way adding "points at infinity" or preventing such an "escape".-An...
of ω1 is ω1+1, just as its one-point compactification (in sharp contrast to ω, whose Stone-Čech compactification is much larger than ω).
Ordinal-indexed sequences
If α is a limit ordinal and X is a set, an α-indexed sequence of elements of X merely means a function from α to X. This concept, a transfinite sequence or ordinal-indexed sequence, is a generalization of the concept of a sequenceSequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
. An ordinary sequence corresponds to the case α = ω.
If X is a topological space, we say that an α-indexed sequence of elements of X converges to a limit x when it converges as a net
Net (mathematics)
In mathematics, more specifically in general topology and related branches, a net or Moore–Smith sequence is a generalization of the notion of a sequence. In essence, a sequence is a function with domain the natural numbers, and in the context of topology, the range of this function is...
, in other words, when given any neighborhood U of x there is an ordinal β<α such that xι is in U for all ι≥β.
Ordinal-indexed sequences are more powerful than ordinary (ω-indexed) sequences to determine limits in topology: for example, ω1 (omega-one, the set of all countable ordinal numbers, and the smallest uncountable ordinal number), is a limit point of ω1+1 (because it is a limit ordinal), and, indeed, it is the limit of the ω1-indexed sequence which maps any ordinal less than ω1 to itself: however, it is not the limit of any ordinary (ω-indexed) sequence in ω1, since any such limit is less than or equal to the union of its elements, which is a countable union of countable sets, hence itself countable.
However, ordinal-indexed sequences are not powerful enough to replace nets (or filters
Filter (mathematics)
In mathematics, a filter is a special subset of a partially ordered set. A frequently used special case is the situation that the ordered set under consideration is just the power set of some set, ordered by set inclusion. Filters appear in order and lattice theory, but can also be found in...
) in general: for example, on the Tychonoff plank
Tychonoff plank
In topology, the Tychonoff plank is a topological space that is a counterexample to several plausible-sounding conjectures. It is defined as the product of the two ordinal space[0,\omega_1]\times[0,\omega]...
(the product space
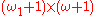), the corner point 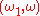is a limit point (it is in the closure) of the open subset 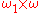, but it is not the limit of an ordinal-indexed sequence.