
Saturated model
Encyclopedia
In mathematical logic
, and particularly in its subfield model theory
, a saturated model M is one which realizes as many complete types as may be "reasonably expected" given its size. For example, an ultrapower model of the hyperreals is countably saturated, meaning that every descending nested sequence of internal set
s has a nonempty intersection, see Goldblatt (1998).
and M a model in some first-order language. Then M is called κ-saturated if for all subsets A ⊆ M of cardinality less than κ, M realizes all complete types over A. The model M is called saturated if it is |M|-saturated where |M| denotes the cardinality of M. That is, it realizes all complete types over sets of parameters of size less than |M|. According to some authors, a model M is called countably saturated if it is -saturated; that is, it realizes all complete types over countable sets of parameters. According to others, it is countably saturated if it is
-saturated; that is, it realizes all complete types over countable sets of parameters. According to others, it is countably saturated if it is 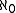 -saturated; i.e. realizes all complete types over finite parameter sets.
-saturated; i.e. realizes all complete types over finite parameter sets.
element of R is, by definition of the word, not definable in the field language). However, they still form a part of the structure, so we need types to describe relationships with them. Thus we allow sets of parameters from the structure in our definition of types. This argument allows us to discuss specific features of the model which we may otherwise miss – for example, a specific increasing sequence cn having a bound can be expressed as realizing the type which uses countably many parameters. If the sequence is not definable, this fact about the structure cannot be described using the base language, so a weakly saturated structure may not bound the sequence, while an ω-saturated structure will.
The reason we only require parameter sets which are strictly smaller than the model is trivial: without this restriction, no infinite model is saturated. Consider a model M, and the type Each finite subset of this type is realized in the (infinite) model M, so by compactness it is consistent with M, but is trivially not realized. Any definition which is universally unsatisfied is useless; hence the restriction.
Both of these theories can be shown to be ω-categorical through the back-and-forth method. This can be generalized as follows: the unique model of cardinality κ of a countable κ-categorical theory is saturated.
However, the statement that every model has a saturated elementary extension is not provable in ZFC. In fact, this statement is equivalent to the existence of a proper class of cardinals κ such that κ<κ = κ. The latter identity implies that either for some λ, or κ is weakly inaccessible.
in the following way: let T be a countable theory in a first-order language (that is, a set of mutually consistent sentences in that language) and let P be a prime model of T. Then P admits an elementary embedding into any other model of T. The equivalent notion for saturated models is that any "reasonably small" model of T is elementarily embedded in a saturated model, where "reasonably small" means cardinality no larger than that of the model in which it is to be embedded. Any saturated model is also homogeneous. However, while for countable theories there is a unique prime model, saturated models are necessarily specific to a particular cardinality. Given certain set-theoretic assumptions, saturated models (albeit of very large cardinality) exist for arbitrary theories. For λ-stable
theories, saturated models of cardinality λ exist.
Mathematical logic
Mathematical logic is a subfield of mathematics with close connections to foundations of mathematics, theoretical computer science and philosophical logic. The field includes both the mathematical study of logic and the applications of formal logic to other areas of mathematics...
, and particularly in its subfield model theory
Model theory
In mathematics, model theory is the study of mathematical structures using tools from mathematical logic....
, a saturated model M is one which realizes as many complete types as may be "reasonably expected" given its size. For example, an ultrapower model of the hyperreals is countably saturated, meaning that every descending nested sequence of internal set
Internal set
In mathematical logic, in particular in model theory and non-standard analysis, an internal set is a set that is a member of a model.Internal set is the key tool in formulating the transfer principle, which concerns the logical relation between the properties of the real numbers R, and the...
s has a nonempty intersection, see Goldblatt (1998).
Definition
Let κ be a finite or infinite cardinal numberCardinal number
In mathematics, cardinal numbers, or cardinals for short, are a generalization of the natural numbers used to measure the cardinality of sets. The cardinality of a finite set is a natural number – the number of elements in the set. The transfinite cardinal numbers describe the sizes of infinite...
and M a model in some first-order language. Then M is called κ-saturated if for all subsets A ⊆ M of cardinality less than κ, M realizes all complete types over A. The model M is called saturated if it is |M|-saturated where |M| denotes the cardinality of M. That is, it realizes all complete types over sets of parameters of size less than |M|. According to some authors, a model M is called countably saturated if it is
 -saturated; that is, it realizes all complete types over countable sets of parameters. According to others, it is countably saturated if it is
-saturated; that is, it realizes all complete types over countable sets of parameters. According to others, it is countably saturated if it is 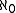 -saturated; i.e. realizes all complete types over finite parameter sets.
-saturated; i.e. realizes all complete types over finite parameter sets.Motivation
The seemingly more intuitive notion – that all complete types of the language are realized – turns out to be too weak (and is, appropriately, named weak saturation, which is the same as 1-saturation). The difference lies in the fact that many structures contain elements which are not definable (for example, any transcendentalTranscendental number
In mathematics, a transcendental number is a number that is not algebraic—that is, it is not a root of a non-constant polynomial equation with rational coefficients. The most prominent examples of transcendental numbers are π and e...
element of R is, by definition of the word, not definable in the field language). However, they still form a part of the structure, so we need types to describe relationships with them. Thus we allow sets of parameters from the structure in our definition of types. This argument allows us to discuss specific features of the model which we may otherwise miss – for example, a specific increasing sequence cn having a bound can be expressed as realizing the type which uses countably many parameters. If the sequence is not definable, this fact about the structure cannot be described using the base language, so a weakly saturated structure may not bound the sequence, while an ω-saturated structure will.
The reason we only require parameter sets which are strictly smaller than the model is trivial: without this restriction, no infinite model is saturated. Consider a model M, and the type Each finite subset of this type is realized in the (infinite) model M, so by compactness it is consistent with M, but is trivially not realized. Any definition which is universally unsatisfied is useless; hence the restriction.
Examples
Saturated models exist for certain theories and cardinalities:- (Q, <) – the set of rational numberRational numberIn mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s with their usual ordering – is saturated. Intuitively, this is because any type consistent with the theory is implied by the order type; that is, the order the variables come in tells you everything there is to know about their role in the structure. - (R, <) – the set of real numberReal numberIn mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s with their usual ordering – is not saturated. For example, take the type (in one variable x) which contains the formula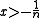 for every natural number n, as well as the formula
for every natural number n, as well as the formula 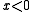 . This type uses ω different parameters from R. Every finite subset of the type is realized on R by some real x, so by compactness it is consistent with the structure, but it is not realized, as it would imply an upper bound to the sequence −1/n which is less than 0 (its least upper bound). Thus (R,<) is not ω1-saturated, and not saturated. However, it is ω-saturated, for essentially the same reason as Q – every finite type is given by the order type, which if consistent, is always realized, because of the density of the order.
. This type uses ω different parameters from R. Every finite subset of the type is realized on R by some real x, so by compactness it is consistent with the structure, but it is not realized, as it would imply an upper bound to the sequence −1/n which is less than 0 (its least upper bound). Thus (R,<) is not ω1-saturated, and not saturated. However, it is ω-saturated, for essentially the same reason as Q – every finite type is given by the order type, which if consistent, is always realized, because of the density of the order. - The countable random graph, with the only non-logical symbol being the edge existence relation, is also saturated, because any complete type is implied by the finite subgraph consisting of the variables and paramaters used to define the type.
Both of these theories can be shown to be ω-categorical through the back-and-forth method. This can be generalized as follows: the unique model of cardinality κ of a countable κ-categorical theory is saturated.
However, the statement that every model has a saturated elementary extension is not provable in ZFC. In fact, this statement is equivalent to the existence of a proper class of cardinals κ such that κ<κ = κ. The latter identity implies that either for some λ, or κ is weakly inaccessible.
Relationship to prime models
The notion of saturated model is dual to the notion of prime modelPrime model
In mathematics, and in particular model theory, a prime model is a model which is as simple as possible. Specifically, a model P is prime if it admits an elementary embedding into any model M to which it is elementarily equivalent .- Cardinality :In contrast with the notion of saturated model,...
in the following way: let T be a countable theory in a first-order language (that is, a set of mutually consistent sentences in that language) and let P be a prime model of T. Then P admits an elementary embedding into any other model of T. The equivalent notion for saturated models is that any "reasonably small" model of T is elementarily embedded in a saturated model, where "reasonably small" means cardinality no larger than that of the model in which it is to be embedded. Any saturated model is also homogeneous. However, while for countable theories there is a unique prime model, saturated models are necessarily specific to a particular cardinality. Given certain set-theoretic assumptions, saturated models (albeit of very large cardinality) exist for arbitrary theories. For λ-stable
Stable theory
In model theory, a complete theory is called stable if it does not have too many types. One goal of classification theory is to divide all complete theories into those whose models can be classified and those whose models are too complicated to classify, and to classify all models in the cases...
theories, saturated models of cardinality λ exist.

