Cardinal number - AbsoluteAstronomy.com

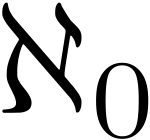
Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, cardinal numbers, or cardinals for short, are a generalization of the natural number

Natural number

In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...

s used to measure the cardinality (size) of sets. The cardinality of a finite set is a natural number – the number of elements in the set. The transfinite cardinal numbers describe the sizes of infinite sets.

Cardinality is defined in terms of bijective functions. Two sets have the same cardinal number if and only if there is a bijection between them. In the case of finite sets, this agrees with the intuitive notion of size. In the case of infinite sets, the behavior is more complex. A fundamental theorem due to Georg Cantor

Georg Cantor

Georg Ferdinand Ludwig Philipp Cantor was a German mathematician, best known as the inventor of set theory, which has become a fundamental theory in mathematics. Cantor established the importance of one-to-one correspondence between the members of two sets, defined infinite and well-ordered sets,...

shows that it is possible for infinite sets to have different cardinalities, and in particular the set of real number

Real number

In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...

s and the set of natural number

Natural number

s do not have the same cardinal number. It is also possible for a proper subset of an infinite set to have the same cardinality as the original set, something that cannot happen with proper subsets of finite sets.

There is a transfinite sequence of cardinal numbers:

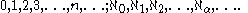
This sequence starts with the natural number

Natural number

s, including zero, (finite cardinals), which are followed by the aleph number

Aleph number

In set theory, a discipline within mathematics, the aleph numbers are a sequence of numbers used to represent the cardinality of infinite sets. They are named after the symbol used to denote them, the Hebrew letter aleph...

s (infinite cardinals of well-ordered sets). The aleph numbers are indexed by ordinal number

Ordinal number

In set theory, an ordinal number, or just ordinal, is the order type of a well-ordered set. They are usually identified with hereditarily transitive sets. Ordinals are an extension of the natural numbers different from integers and from cardinals...

s. Under the assumption of the axiom of choice, this transfinite sequence includes every cardinal number. If one rejects that axiom, the situation is more complicated, with additional infinite cardinals that are not alephs.

Cardinality is studied for its own sake as part of set theory

Set theory

Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...

. It is also a tool used in branches of mathematics including combinatorics

Combinatorics

Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...

, abstract algebra

Abstract algebra

Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...

, and mathematical analysis

Mathematical analysis

Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...

History

The notion of cardinality, as now understood, was formulated by Georg Cantor

Georg Cantor

, the originator of set theory

Set theory

, in 1874–1884. Cantor first established cardinality as an instrument to compare finite sets; e.g. the sets {1,2,3} and {2,3,4} are not equal, but have the same cardinality: three.

Cantor identified the fact that one-to-one correspondence

Bijection

A bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...

is the way to tell that two sets have the same size, called "cardinality", in the case of finite sets. Using this one-to-one correspondence, he applied the concept to infinite sets; e.g. the set of natural numbers N = {0, 1, 2, 3, ...}. He called these cardinal numbers transfinite cardinal numbers, and defined all sets having a one-to-one correspondence with N to be denumerable (countably infinite) sets

Countable set

In mathematics, a countable set is a set with the same cardinality as some subset of the set of natural numbers. A set that is not countable is called uncountable. The term was originated by Georg Cantor...

.

Naming this cardinal number

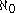, aleph-null

Aleph number

, Cantor proved that any unbounded subset of N has the same cardinality as N, even if this might appear at first glance to run contrary to intuition. He also proved that the set of all ordered pair

Ordered pair

In mathematics, an ordered pair is a pair of mathematical objects. In the ordered pair , the object a is called the first entry, and the object b the second entry of the pair...

s of natural numbers is denumerable (which implies that the set of all rational number

Rational number

In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...

s is denumerable), and later proved that the set of all algebraic number

Algebraic number

In mathematics, an algebraic number is a number that is a root of a non-zero polynomial in one variable with rational coefficients. Numbers such as π that are not algebraic are said to be transcendental; almost all real numbers are transcendental...

s is also denumerable. Each algebraic number z may be encoded as a finite sequence of integers which are the coefficients in the polynomial equation of which it is the solution, i.e. the ordered n-tuple

together with a pair of rationals

such that z is the unique root of the polynomial with coefficients

that lies in the interval

.

In his 1874 paper, Cantor proved that there exist higher-order cardinal numbers by showing that the set of real numbers has cardinality greater than that of N. His original presentation

Cantor's first uncountability proof

Georg Cantor's first uncountability proof demonstrates that the set of all real numbers is uncountable. This proof differs from the more familiar proof that uses his diagonal argument...

used a complex argument with nested intervals

Nested intervals

In mathematics, a sequence of nested intervals is understood as a collection of sets of real numberssuch that each set In is an interval of the real line, for n = 1, 2, 3, ... , and that furtherfor all n...

, but in an 1891 paper he proved the same result using his ingenious but simple diagonal argument

Cantor's diagonal argument

Cantor's diagonal argument, also called the diagonalisation argument, the diagonal slash argument or the diagonal method, was published in 1891 by Georg Cantor as a mathematical proof that there are infinite sets which cannot be put into one-to-one correspondence with the infinite set of natural...

. This new cardinal number, called the cardinality of the continuum

Cardinality of the continuum

In set theory, the cardinality of the continuum is the cardinality or “size” of the set of real numbers \mathbb R, sometimes called the continuum. It is an infinite cardinal number and is denoted by |\mathbb R| or \mathfrak c ....

, was termed

by Cantor.

Cantor also developed a large portion of the general theory of cardinal numbers; he proved that there is a smallest transfinite cardinal number (

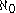, aleph-null) and that for every cardinal number, there is a next-larger cardinal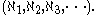

His continuum hypothesis

Continuum hypothesis

In mathematics, the continuum hypothesis is a hypothesis, advanced by Georg Cantor in 1874, about the possible sizes of infinite sets. It states:Establishing the truth or falsehood of the continuum hypothesis is the first of Hilbert's 23 problems presented in the year 1900...

is the proposition that

is the same as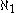

, but this has been found to be independent of the standard axioms of mathematical set theory; it can neither be proved nor disproved under the standard assumptions.

Motivation

In informal use, a cardinal number is what is normally referred to as a counting number, provided that 0 is included: 0, 1, 2, .... They may be identified with the natural numbers beginning with 0.
The counting numbers are exactly what can be defined formally as the finite cardinal numbers. Infinite cardinals only occur in higher-level mathematics and logic.

More formally, a non-zero number can be used for two purposes: to describe the size of a set, or to describe the position of an element in a sequence. For finite sets and sequences it is easy to see that these two notions coincide, since for every number describing a position in a sequence we can construct a set which has exactly the right size, e.g. 3 describes the position of 'c' in the sequence <'a','b','c','d',...>, and we can construct the set {a,b,c} which has 3 elements. However when dealing with infinite sets it is essential to distinguish between the two — the two notions are in fact different for infinite sets. Considering the position aspect leads to ordinal numbers, while the size aspect is generalized by the cardinal numbers described here.

The intuition behind the formal definition of cardinal is the construction of a notion of the relative size or "bigness" of a set without reference to the kind of members which it has. For finite sets this is easy; one simply counts the number of elements a set has. In order to compare the sizes of larger sets, it is necessary to appeal to more subtle notions.

A set Y is at least as big as, or greater than or equal to a set X if there is an injective

Injective function

In mathematics, an injective function is a function that preserves distinctness: it never maps distinct elements of its domain to the same element of its codomain. In other words, every element of the function's codomain is mapped to by at most one element of its domain...

(one-to-one) mapping

Map (mathematics)

In most of mathematics and in some related technical fields, the term mapping, usually shortened to map, is either a synonym for function, or denotes a particular kind of function which is important in that branch, or denotes something conceptually similar to a function.In graph theory, a map is a...

from the elements of X to the elements of Y. A one-to-one mapping identifies each element of the set X with a unique element of the set Y. This is most easily understood by an example; suppose we have the sets X = {1,2,3} and Y = {a,b,c,d}, then using this notion of size we would observe that there is a mapping:

1 → a

2 → b

3 → c

which is one-to-one, and hence conclude that Y has cardinality greater than or equal to X. Note the element d has no element mapping to it, but this is permitted as we only require a one-to-one mapping, and not necessarily a one-to-one and onto mapping. The advantage of this notion is that it can be extended to infinite sets.

We can then extend this to an equality-style relation.
Two sets X and Y are said to have the same cardinality if there exists a bijection

Bijection

between X and Y. By the Schroeder-Bernstein theorem, this is equivalent to there being both a one-to-one mapping from X to Y and a one-to-one mapping from Y to X.
We then write | X | = | Y |. The cardinal number of X itself is often defined as the least ordinal a with | a | = | X |. This is called the von Neumann cardinal assignment

Von Neumann cardinal assignment

The von Neumann cardinal assignment is a cardinal assignment which uses ordinal numbers. For a well-ordered set U, we define its cardinal number to be the smallest ordinal number equinumerous to U. More precisely:...

; for this definition to make sense, it must be proved that every set has the same cardinality as some ordinal; this statement is the well-ordering principle

Well-ordering principle

The "well-ordering principle" is a property of ordered sets. A set X is well ordered if every subset of X has a least element. An example of a well ordered set is the set of natural numbers. An example of set that is not well ordered is the set of integers...

. It is however possible to discuss the relative cardinality of sets without explicitly assigning names to objects.

The classic example used is that of the infinite hotel paradox, also called Hilbert's paradox of the Grand Hotel

Hilbert's paradox of the Grand Hotel

Hilbert's paradox of the Grand Hotel is a mathematical veridical paradox about infinite sets presented by German mathematician David Hilbert .-The paradox:...

. Suppose you are an innkeeper at a hotel with an infinite number of rooms. The hotel is full, and then a new guest arrives. It's possible to fit the extra guest in by asking the guest who was in room 1 to move to room 2, the guest in room 2 to move to room 3, and so on, leaving room 1 vacant. We can explicitly write a segment of this mapping:

1 ↔ 2

2 ↔ 3

3 ↔ 4

...

n ↔ n+1

...

In this way we can see that the set {1,2,3,...} has the same cardinality as the set {2,3,4,...} since a bijection between the first and the second has been shown. This motivates the definition of an infinite set being any set which has a proper subset of the same cardinality; in this case {2,3,4,...} is a proper subset of {1,2,3,...}.

When considering these large objects, we might also want to see if the notion of counting order coincides with that of cardinal defined above for these infinite sets. It happens that it doesn't; by considering the above example we can see that if some object "one greater than infinity" exists, then it must have the same cardinality as the infinite set we started out with. It is possible to use a different formal notion for number, called ordinals

Ordinal number

, based on the ideas of counting and considering each number in turn, and we discover that the notions of cardinality and ordinality are divergent once we move out of the finite numbers.

It can be proved that the cardinality of the real number

Real number

In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...

s is greater than that of the natural numbers just described. This can be visualized using Cantor's diagonal argument

Cantor's diagonal argument

;
classic questions of cardinality (for instance the continuum hypothesis

Continuum hypothesis

) are concerned with discovering whether there is some cardinal between some pair of other infinite cardinals. In more recent times mathematicians have been describing the properties of larger and larger cardinals.

Since cardinality is such a common concept in mathematics, a variety of names are in use. Sameness of cardinality is sometimes referred to as equipotence, equipollence, or equinumerosity. It is thus said that two sets with the same cardinality are, respectively, equipotent, equipollent, or equinumerous.

Formal definition

Formally, assuming the axiom of choice, the cardinality of a set X is the least ordinal α such that there is a bijection between X and α. This definition is known as the von Neumann cardinal assignment

Von Neumann cardinal assignment

. If the axiom of choice is not assumed we need to do something different. The oldest definition of the cardinality of a set X (implicit in Cantor and explicit in Frege and Principia Mathematica

Principia Mathematica

The Principia Mathematica is a three-volume work on the foundations of mathematics, written by Alfred North Whitehead and Bertrand Russell and published in 1910, 1912, and 1913...

) is as the class [X] of all sets that are equinumerous with X. This does not work in ZFC or other related systems of axiomatic set theory because if X is non-empty, this collection is too large to be a set. In fact, for X ≠ ∅ there is an injection from the universe into [X] by mapping a set m to {m} × X and so by limitation of size

Limitation of size

In the philosophy of mathematics, specifically the philosophical foundations of set theory, limitation of size is a concept developed by Philip Jourdain and/or Georg Cantor to avoid Cantor's paradox. It identifies certain "inconsistent multiplicities", in Cantor's terminology, that cannot be sets...

, [X] is a proper class. The definition does work however in type theory

Type theory

In mathematics, logic and computer science, type theory is any of several formal systems that can serve as alternatives to naive set theory, or the study of such formalisms in general...

and in New Foundations

New Foundations

In mathematical logic, New Foundations is an axiomatic set theory, conceived by Willard Van Orman Quine as a simplification of the theory of types of Principia Mathematica. Quine first proposed NF in a 1937 article titled "New Foundations for Mathematical Logic"; hence the name...

and related systems. However, if we restrict from this class to those equinumerous with X that have the least rank, then it will work (this is a trick due to Dana Scott

Dana Scott

Dana Stewart Scott is the emeritus Hillman University Professor of Computer Science, Philosophy, and Mathematical Logic at Carnegie Mellon University; he is now retired and lives in Berkeley, California...

: it works because the collection of objects with any given rank is a set).

Formally, the order among cardinal numbers is defined as follows: | X | ≤ | Y | means that there exists an injective function from X to Y. The Cantor–Bernstein–Schroeder theorem

Cantor–Bernstein–Schroeder theorem

In set theory, the Cantor–Bernstein–Schroeder theorem, named after Georg Cantor, Felix Bernstein, and Ernst Schröder, states that, if there exist injective functions and between the sets A and B, then there exists a bijective function...

states that if | X | ≤ | Y | and | Y | ≤ | X | then | X | = | Y |. The axiom of choice is equivalent to the statement that given two sets X and Y, either | X | ≤ | Y | or | Y | ≤ | X |.

A set X is Dedekind-infinite if there exists a proper subset Y of X with | X | = | Y |, and Dedekind-finite if such a subset doesn't exist. The finite cardinals are just the natural numbers, i.e., a set X is finite if and only if | X | = | n | = n for some natural number n. Any other set is infinite. Assuming the axiom of choice, it can be proved that the Dedekind notions correspond to the standard ones. It can also be proved that the cardinal

(aleph null or aleph-0, where aleph is the first letter in the Hebrew alphabet

Hebrew alphabet

The Hebrew alphabet , known variously by scholars as the Jewish script, square script, block script, or more historically, the Assyrian script, is used in the writing of the Hebrew language, as well as other Jewish languages, most notably Yiddish, Ladino, and Judeo-Arabic. There have been two...

, represented

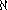) of the set of natural numbers is the smallest infinite cardinal, i.e. that any infinite set has a subset of cardinality

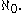The next larger cardinal is denoted by

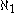and so on. For every ordinal

Ordinal number

α there is a cardinal number

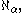and this list exhausts all infinite cardinal numbers.

Cardinal arithmetic

We can define arithmetic

Arithmetic

Arithmetic or arithmetics is the oldest and most elementary branch of mathematics, used by almost everyone, for tasks ranging from simple day-to-day counting to advanced science and business calculations. It involves the study of quantity, especially as the result of combining numbers...

operations on cardinal numbers that generalize the ordinary operations for natural numbers. It can be shown that for finite cardinals these operations coincide with the usual operations for natural numbers. Furthermore, these operations share many properties with ordinary arithmetic.

Successor cardinal

If the axiom of choice holds, every cardinal κ has a successor κ⁺ > κ, and there are no cardinals between κ and its successor. For finite cardinals, the successor is simply κ+1. For infinite cardinals, the successor cardinal differs from the successor ordinal

Successor ordinal

In set theory, the successor of an ordinal number α is the smallest ordinal number greater than α. An ordinal number that is a successor is called a successor ordinal...

Cardinal addition

If X and Y are disjoint, addition is given by the union

Union (set theory)

In set theory, the union of a collection of sets is the set of all distinct elements in the collection. The union of a collection of sets S_1, S_2, S_3, \dots , S_n\,\! gives a set S_1 \cup S_2 \cup S_3 \cup \dots \cup S_n.- Definition :...

of X and Y. If the two sets are not already disjoint, then they can be replaced by disjoint sets of the same cardinality, e.g., replace X by X×{0} and Y by Y×{1}.

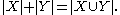
Zero is an additive identity κ + 0 = 0 + κ = κ.

Addition is associative (κ + μ) + ν = κ + (μ + ν).

Addition is commutative κ + μ = μ + κ.

Addition is non-decreasing in both arguments:

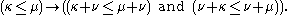
Assuming the axiom of choice, addition of infinite cardinal numbers is easy. If either

is infinite, then

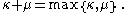
Subtraction

Assuming the axiom of choice and, given an infinite cardinal σ and a cardinal μ, there exists a cardinal κ such that μ + κ = σ if and only if μ ≤ σ. It will be unique (and equal to σ) if and only if μ < σ.

Cardinal multiplication

The product of cardinals comes from the cartesian product

Cartesian product

In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...

κ·0 = 0·κ = 0.

κ·μ = 0

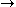(κ = 0 or μ = 0).

One is a multiplicative identity κ·1 = 1·κ = κ.

Multiplication is associative (κ·μ)·ν = κ·(μ·ν).

Multiplication is commutative κ·μ = μ·κ.

Multiplication is non-decreasing in both arguments:
κ ≤ μ

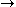(κ·ν ≤ μ·ν and ν·κ ≤ ν·μ).

Multiplication distributes

Distributivity

In mathematics, and in particular in abstract algebra, distributivity is a property of binary operations that generalizes the distributive law from elementary algebra.For example:...

over addition:
κ·(μ + ν) = κ·μ + κ·ν and
(μ + ν)·κ = μ·κ + ν·κ.

Assuming the axiom of choice, multiplication of infinite cardinal numbers is also easy. If either κ or μ is infinite and both are non-zero, then

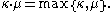
Division

Assuming the axiom of choice and, given an infinite cardinal π and a non-zero cardinal μ, there exists a cardinal κ such that μ · κ = π if and only if μ ≤ π. It will be unique (and equal to π) if and only if μ < π.

Cardinal exponentiation

Exponentiation is given by

where X^Y is the set of all functions

Function (mathematics)

In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...

from Y to X.

κ⁰ = 1 (in particular 0⁰ = 1), see empty function

Empty function

In mathematics, an empty function is a function whose domain is the empty set. For each set A, there is exactly one such empty functionf_A: \varnothing \rightarrow A....

If 1 ≤ μ, then 0^μ = 0.

1^μ = 1.

κ¹ = κ.

κ^{μ + ν} = κ^μ·κ^ν.

κ^μ·ν = (κ^μ)^ν.^ν = κ^ν·μ^ν.

Exponentiation is non-decreasing in both arguments:

(ν^κ ≤ ν^μ) and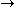

(κ^ν ≤ μ^ν).

Note that 2^| X | is the cardinality of the power set of the set X and Cantor's diagonal argument

Cantor's diagonal argument

shows that 2^| X | > | X | for any set X. This proves that no largest cardinal exists (because for any cardinal κ, we can always find a larger cardinal 2^κ). In fact, the class

Class (set theory)

In set theory and its applications throughout mathematics, a class is a collection of sets which can be unambiguously defined by a property that all its members share. The precise definition of "class" depends on foundational context...

of cardinals is a proper class.

All the remaining propositions in this section assume the axiom of choice:

If κ and μ are both finite and greater than 1, and ν is infinite, then κ^ν = μ^ν.

If κ is infinite and μ is finite and non-zero, then κ^μ = κ.

If 2 ≤ κ and 1 ≤ μ and at least one of them is infinite, then:

Max (κ, 2^μ) ≤ κ^μ ≤ Max (2^κ, 2^μ).

Using König's theorem

König's theorem (set theory)

In set theory, König's theorem colloquially states that if the axiom of choice holds, I is a set, mi and ni are cardinal numbers for every i in I, and m_i In set theory, König's theorem In set theory, König's theorem (named after the Hungarian mathematician Gyula Kőnig, who published under the...

, one can prove κ < κ^cf(κ) and κ < cf(2^κ) for any infinite cardinal κ, where cf(κ) is the cofinality

Cofinality

In mathematics, especially in order theory, the cofinality cf of a partially ordered set A is the least of the cardinalities of the cofinal subsets of A....

of κ.

Roots

Assuming the axiom of choice and, given an infinite cardinal

and a finite cardinal

greater than 0, the cardinal

satisfying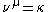

will be

Logarithms

Assuming the axiom of choice and, given an infinite cardinal

and a finite cardinal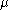

greater than 1, there may or may not be a cardinal

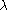satisfying

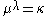. But, if such a cardinal exists, it is infinite and less than

and any finite cardinality

greater than 1 will also satisfy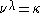

.

The logarithm of an infinite cardinal number κ is defined as the least cardinal number μ such that κ ≤ 2^μ. Logarithms of infinite cardinals are useful in some fields of mathematics, for example in the study of cardinal invariants of topological spaces, though they lack some of the properties that logarithms of positive real numbers possess.

The continuum hypothesis

Continuum hypothesis

(CH) states that there are no cardinals strictly between

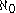and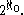

The latter cardinal number is also often denoted by

; it is the cardinality of the continuum

Cardinality of the continuum

(the set of real number

Real number

In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...

s). In this case

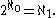The generalized continuum hypothesis (GCH) states that for every infinite set X, there are no cardinals strictly between | X | and 2^| X |.
The continuum hypothesis is independent of the usual axioms of set theory, the Zermelo-Fraenkel axioms together with the axiom of choice (ZFC).

External links

Cardinality at ProvenMath formal proofs of the basic theorems on cardinality.
Undergraduate Set Theory more proofs about cardinality - includes proof of infinite cardinal addition in Section 4.2.

The source of this article is wikipedia, the free encyclopedia. The text of this article is licensed under the GFDL.

History

Motivation

Formal definition

Cardinal arithmetic

Successor cardinal

Cardinal addition

Subtraction

Cardinal multiplication

Division

Cardinal exponentiation

Roots

Logarithms

The continuum hypothesis

See also

External links