Freudenthal magic square
Encyclopedia
In mathematics
, the Freudenthal magic square (or Freudenthal–Tits magic square) is a construction relating several Lie groups. It is named after Hans Freudenthal
and Jacques Tits
, who developed the idea independently. It associates a Lie group (or corresponding Lie algebra) to a pair of division algebras A, B. The resulting Lie algebras have Dynkin diagrams according to the following table.
The Freudenthal magic square includes all of the exceptional Lie groups apart from G2, and it provides one possible approach to justify the assertion that "the exceptional Lie groups all exist because of the octonions": G2 itself is the automorphism group of the octonions (also, it is in many ways like a classical Lie group because it is the stabilizer of a generic 3-form on a 7-dimensional vector space – see prehomogeneous vector space
).
A (i.e., R, C, H or O) there is a Jordan algebra
of 3×3 A-Hermitian matrices. For any pair
of such division algebras, one can define a Lie algebra
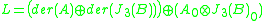
where der denotes the Lie algebra of derivation
s of an algebra, and the subscript 0 denotes the trace-free part. The Lie algebra L has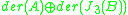
as a subalgebra, and this acts naturally on 
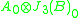. The Lie bracket on 
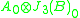(which is not a subalgebra) is not obvious, but Tits showed how it could be defined, and that it produced the following table of compact Lie algebra
s.
Note that by construction, the row of the table with A=R gives der(J3(B)), and similarly vice versa.
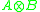, denoted 
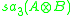. Vinberg defines a Lie algebra structure on
When A and B have no derivations (i.e., R or C), this is just the Lie (commutator) bracket on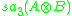
. In the presence of derivations, these form a subalgebra acting naturally on 
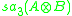as in Tits' construction, and the tracefree commutator bracket on 
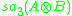is modified by an expression with values in 
.
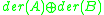and developed by Chris Barton and Anthony Sudbery, uses triality
in the form developed by John Frank Adams. Whereas Vinberg's construction is based on the automorphism groups of a division algebra A (or rather their Lie algebras of derivations), Barton and Sudbery use the group of automorphisms of the corresponding triality. The triality is the trilinear map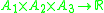
obtained by taking three copies of the division algebra A, and using the inner product on A to dualize the multiplication. The automorphism group is the subgroup of SO(A1)×SO(A2)×SO(A3) preserving this trilinear map. It is denoted Tri(A). The following table compares its Lie algebra to the Lie algebra of derivations.
Barton and Sudbery then identify the magic square Lie algebra corresponding to (A,B) with a Lie algebra structure on the vector space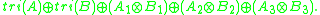
The Lie bracket is compatible with a Z2×Z2 grading, with tri(A) and tri(B) in degree (0,0), and the three copies of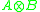
in degrees (0,1), (1,0) and (1,1). The bracket preserves tri(A) and tri(B) and these act naturally on the three copies of 
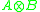, as in the other constructions, but the brackets between these three copies are more constrained.
For instance when A and B are the octonions, the triality is that of Spin(8), the double cover of SO8, and the Barton-Sudbery description yields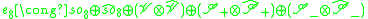
where V, S+ and S- are the three 8 dimensional representations of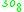
(the fundamental representation and the two spin representations), and the hatted objects are an isomorphic copy.
With respect to one of the Z2 gradings, the first three summands combine to give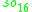
and the last two together form one of its spin representations Δ+128 (the superscript denotes the dimension). This is a well known symmetric decomposition
of E8
.
The Barton-Sudbery construction extends this to the other Lie algebras in the magic square. In particular, for the exceptional Lie algebras in the last row (or column), the symmetric decompositions are: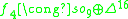
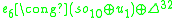
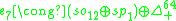
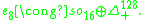
s, there are other composition algebra
s over R, namely the split-complex number
s, the split-quaternions and the split-octonions. If one uses these instead of the complex numbers, quaternions, and octonions, one obtains the following variant of the magic square (where the split versions of the division algebras are denoted by a dash).
Here all the Lie algebras are the split real form except for so3, but a sign change in the definition of the Lie bracket can be used to produce the split form so2,1. In particular, for the exceptional Lie algebras, the maximal compact subalgebras are as follows:
A non-symmetric version of the magic square can also be obtained by combining the split algebras with the usual division algebras. According to Barton and Sudbery, the resulting table of Lie algebras is as follows.
The real exceptional Lie algebras appearing here can again be described by their maximal compact subalgebras.
K. This yields the following magic square.
There is some ambiguity here if K is not algebraically closed. In the case K=C, this is the complexification of the Freudenthal magic squares for R discussed so far.
For n=2, J2(O) is also a Jordan algebra. In the compact case (over R) this yields a magic square of orthogonal Lie algebras.
The last row and column here are the orthogonal algebra part of the isotropy algebra in the symmetric decomposition of the exceptional Lie algebras mentioned previously.
These constructions are closely related to hermitian symmetric space
s – cf. prehomogeneous vector space
s.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Freudenthal magic square (or Freudenthal–Tits magic square) is a construction relating several Lie groups. It is named after Hans Freudenthal
Hans Freudenthal
Hans Freudenthal was a Dutch mathematician. He made substantial contributions to algebraic topology and also took an interest in literature, philosophy, history and mathematics education....
and Jacques Tits
Jacques Tits
Jacques Tits is a Belgian and French mathematician who works on group theory and geometry and who introduced Tits buildings, the Tits alternative, and the Tits group.- Career :Tits received his doctorate in mathematics at the age of 20...
, who developed the idea independently. It associates a Lie group (or corresponding Lie algebra) to a pair of division algebras A, B. The resulting Lie algebras have Dynkin diagrams according to the following table.
| A \ B | R | C | H | O |
|---|---|---|---|---|
| R | A1 | A2 | C3 | F4 |
| C | A2 | A2 × A2 | A5 | E6 |
| H | C3 | A5 | D6 | E7 |
| O | F4 | E6 | E7 | E8 |
The Freudenthal magic square includes all of the exceptional Lie groups apart from G2, and it provides one possible approach to justify the assertion that "the exceptional Lie groups all exist because of the octonions": G2 itself is the automorphism group of the octonions (also, it is in many ways like a classical Lie group because it is the stabilizer of a generic 3-form on a 7-dimensional vector space – see prehomogeneous vector space
Prehomogeneous vector space
In mathematics, a prehomogeneous vector space is a finite-dimensional vector space V together with a subgroup G of GL such that G has an open dense orbit in V. Prehomogeneous vector spaces were introduced by Mikio Sato in 1970 and have many applications in geometry, number theory and analysis, as...
).
Tits' approach
Associated with any normed real division algebraDivision algebra
In the field of mathematics called abstract algebra, a division algebra is, roughly speaking, an algebra over a field, in which division is possible.- Definitions :...
A (i.e., R, C, H or O) there is a Jordan algebra
Jordan algebra
In abstract algebra, a Jordan algebra is an algebra over a field whose multiplication satisfies the following axioms:# xy = yx # = x ....
- J3(A)
of 3×3 A-Hermitian matrices. For any pair
of such division algebras, one can define a Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
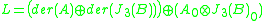
where der denotes the Lie algebra of derivation
Derivation
Derivation may refer to:* Derivation , a function on an algebra which generalizes certain features of the derivative operator* Derivation * Derivation in differential algebra, a unary function satisfying the Leibniz product law...
s of an algebra, and the subscript 0 denotes the trace-free part. The Lie algebra L has
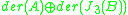as a subalgebra, and this acts naturally on 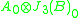. The Lie bracket on 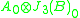(which is not a subalgebra) is not obvious, but Tits showed how it could be defined, and that it produced the following table of compact Lie algebraCompact Lie algebra
In the mathematical field of Lie theory, a Lie algebra is compact if it is the Lie algebra of a compact Lie group. Intrinsically, a compact Lie algebra is a real Lie algebra whose Killing form is negative definite, though this definition does not quite agree with the previous...
s.
| B | R | C | H | O | |
|---|---|---|---|---|---|
| A | der(A/B) | 0 | 0 |  |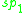
 |
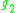| R | 0 |  |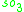
 |
 |
 |
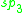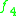| C | 0 |  |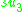
 |
 |
 |
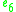| H |  |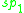
 |
 |
 |
 |
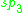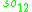| O |  |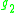
 |
 |
 |
 |
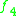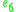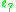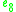Note that by construction, the row of the table with A=R gives der(J3(B)), and similarly vice versa.
Vinberg's symmetric method
The "magic" of the Freudenthal magic square is that the constructed Lie algebra is symmetric in A and B. This is not obvious from Tits' construction. Ernest Vinberg gave a construction which is manifestly symmetric. Instead of using a Jordan algebra, he uses an algebra of skew-hermitian trace-free matrices with entries in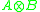, denoted 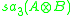. Vinberg defines a Lie algebra structure onWhen A and B have no derivations (i.e., R or C), this is just the Lie (commutator) bracket on
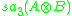. In the presence of derivations, these form a subalgebra acting naturally on 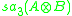as in Tits' construction, and the tracefree commutator bracket on 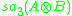is modified by an expression with values in 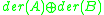.Triality
A more recent construction, suggested by Pierre RamondPierre Ramond
Pierre Ramond is a Distinguished Professor of Physics at University of Florida in Gainesville, Florida...
and developed by Chris Barton and Anthony Sudbery, uses triality
Triality
In mathematics, triality is a relationship between three vector spaces, analogous to the duality relation between dual vector spaces. Most commonly, it describes those special features of the Dynkin diagram D4 and the associated Lie group Spin, the double cover of 8-dimensional rotation group SO,...
in the form developed by John Frank Adams. Whereas Vinberg's construction is based on the automorphism groups of a division algebra A (or rather their Lie algebras of derivations), Barton and Sudbery use the group of automorphisms of the corresponding triality. The triality is the trilinear map
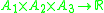
obtained by taking three copies of the division algebra A, and using the inner product on A to dualize the multiplication. The automorphism group is the subgroup of SO(A1)×SO(A2)×SO(A3) preserving this trilinear map. It is denoted Tri(A). The following table compares its Lie algebra to the Lie algebra of derivations.
| A: | R | C | H | O |
|---|---|---|---|---|
 |
0 | 0 |  |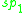
 |
 |
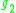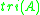0 |  |
 |
 |
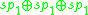Barton and Sudbery then identify the magic square Lie algebra corresponding to (A,B) with a Lie algebra structure on the vector space
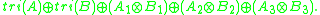
The Lie bracket is compatible with a Z2×Z2 grading, with tri(A) and tri(B) in degree (0,0), and the three copies of
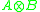in degrees (0,1), (1,0) and (1,1). The bracket preserves tri(A) and tri(B) and these act naturally on the three copies of 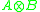, as in the other constructions, but the brackets between these three copies are more constrained.For instance when A and B are the octonions, the triality is that of Spin(8), the double cover of SO8, and the Barton-Sudbery description yields
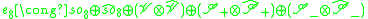
where V, S+ and S- are the three 8 dimensional representations of
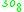(the fundamental representation and the two spin representations), and the hatted objects are an isomorphic copy.With respect to one of the Z2 gradings, the first three summands combine to give
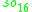and the last two together form one of its spin representations Δ+128 (the superscript denotes the dimension). This is a well known symmetric decompositionRiemannian symmetric space
In differential geometry, representation theory and harmonic analysis, a symmetric space is a smooth manifold whose group of symmetries contains an inversion symmetry about every point. There are two ways to formulate the inversion symmetry, via Riemannian geometry or via Lie theory...
of E8
E8 (mathematics)
In mathematics, E8 is any of several closely related exceptional simple Lie groups, linear algebraic groups or Lie algebras of dimension 248; the same notation is used for the corresponding root lattice, which has rank 8...
.
The Barton-Sudbery construction extends this to the other Lie algebras in the magic square. In particular, for the exceptional Lie algebras in the last row (or column), the symmetric decompositions are:
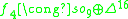
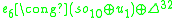
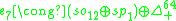
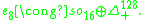
Split composition algebras
In addition to the normed division algebraNormed division algebra
In mathematics, a normed division algebra A is a division algebra over the real or complex numbers which is also a normed vector space, with norm || · || satisfying the following property:\|xy\| = \|x\| \|y\| for all x and y in A....
s, there are other composition algebra
Composition algebra
In mathematics, a composition algebra A over a field K is a unital algebra over K together with a nondegenerate quadratic form N which satisfiesN = NN\,...
s over R, namely the split-complex number
Split-complex number
In abstract algebra, the split-complex numbers are a two-dimensional commutative algebra over the real numbers different from the complex numbers. Every split-complex number has the formwhere x and y are real numbers...
s, the split-quaternions and the split-octonions. If one uses these instead of the complex numbers, quaternions, and octonions, one obtains the following variant of the magic square (where the split versions of the division algebras are denoted by a dash).
| A\B | R | C' | H' | O' |
|---|---|---|---|---|
| R |  |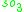
 |
 |
 |
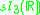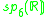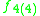| C' |  |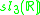
 |
 |
 |
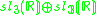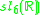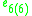| H' |  |
 |
 |
 |
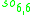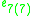| O' |  |
 |
 |
 |
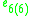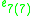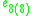Here all the Lie algebras are the split real form except for so3, but a sign change in the definition of the Lie bracket can be used to produce the split form so2,1. In particular, for the exceptional Lie algebras, the maximal compact subalgebras are as follows:
| Split form |  |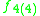
 |
 |
 |
|---|---|---|---|---|
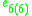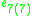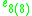| Maximal compact |  |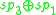
 |
 |
 |
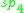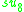A non-symmetric version of the magic square can also be obtained by combining the split algebras with the usual division algebras. According to Barton and Sudbery, the resulting table of Lie algebras is as follows.
| A\B | R | C | H | O |
|---|---|---|---|---|
| R |  |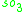
 |
 |
 |
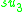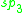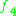| C' |  |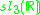
 |
 |
 |
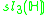| H' |  |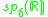
 |
 |
 |
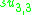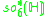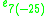| O' |  |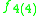
 |
 |
 |
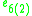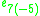The real exceptional Lie algebras appearing here can again be described by their maximal compact subalgebras.
| Lie algebra |  |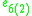
 |
 |
 |
 |
|---|---|---|---|---|---|
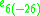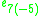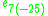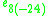| Maximal compact |  |
 |
 |
 |
 |
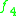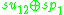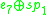Arbitrary fields
The split forms of the composition algebras and Lie algebras can be defined over any fieldField (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
K. This yields the following magic square.
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
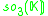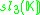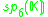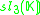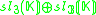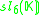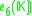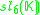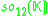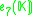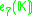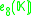There is some ambiguity here if K is not algebraically closed. In the case K=C, this is the complexification of the Freudenthal magic squares for R discussed so far.
More general Jordan algebras
The squares discussed so far are related to the Jordan algebras J3(A), where A is a division algebra. There are also Jordan algebras Jn(A), for any positive integer n, as long as A is associative. These yield split forms (over any field K) and compact forms (over R) of generalized magic squares. |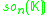
 |
 |
 |
 |
 |
 |
 |
 |
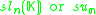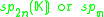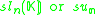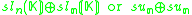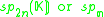For n=2, J2(O) is also a Jordan algebra. In the compact case (over R) this yields a magic square of orthogonal Lie algebras.
| A\B | R | C | H | O |
|---|---|---|---|---|
| R |  |
 |
 |
 |
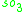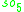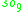| C |  |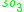
 |
 |
 |
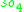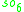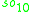| H |  |
 |
 |
 |
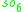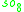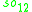| O |  |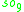
 |
 |
 |
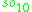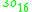The last row and column here are the orthogonal algebra part of the isotropy algebra in the symmetric decomposition of the exceptional Lie algebras mentioned previously.
These constructions are closely related to hermitian symmetric space
Hermitian symmetric space
In mathematics, a Hermitian symmetric space is a Kähler manifold M which, as a Riemannian manifold, is a Riemannian symmetric space. Equivalently, M is a Riemannian symmetric space with a parallel complex structure with respect to which the Riemannian metric is Hermitian...
s – cf. prehomogeneous vector space
Prehomogeneous vector space
In mathematics, a prehomogeneous vector space is a finite-dimensional vector space V together with a subgroup G of GL such that G has an open dense orbit in V. Prehomogeneous vector spaces were introduced by Mikio Sato in 1970 and have many applications in geometry, number theory and analysis, as...
s.
See also
- E8 (mathematics)E8 (mathematics)In mathematics, E8 is any of several closely related exceptional simple Lie groups, linear algebraic groups or Lie algebras of dimension 248; the same notation is used for the corresponding root lattice, which has rank 8...
- E7 (mathematics)
- E6 (mathematics)
- F4 (mathematics)
- G2 (mathematics)
- Jordan triple system