
Albert algebra
Encyclopedia
In mathematics
, an Albert algebra is a 27-dimensional exceptional
Jordan algebra
. They are named after Abraham Adrian Albert
, who pioneered the study of non-associative algebras, usually working over the real numbers. Over the real numbers, there are two such Jordan algebras up to
isomorphism
. One of them, which was first mentioned by and studied by , is the set of 3×3 self-adjoint
matrices over the octonions, equipped with the binary operation
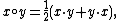
where denotes matrix multiplication. The other is defined the same way, but using split octonions instead of octonions.
denotes matrix multiplication. The other is defined the same way, but using split octonions instead of octonions.
Over any algebraically closed field, there is just one Albert algebra. For example, if we complexify
the two Albert algebras over the real numbers, we obtain isomorphic Albert algebras over the complex numbers.
The Tits–Koecher construction applied to an Albert algebra gives a form of the E7 Lie algebra.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, an Albert algebra is a 27-dimensional exceptional
Exceptional object
Many branches of mathematics study objects of a given type and prove a classification theorem. A common theme is that the classification results in a number of series of objects as well as a finite number of exceptions that don't fit into any series. These are known as exceptional...
Jordan algebra
Jordan algebra
In abstract algebra, a Jordan algebra is an algebra over a field whose multiplication satisfies the following axioms:# xy = yx # = x ....
. They are named after Abraham Adrian Albert
Abraham Adrian Albert
Abraham Adrian Albert was an American mathematician. In 1939, he received the first American Mathematical Society's Cole Prize in Algebra for his work on Riemann matrices...
, who pioneered the study of non-associative algebras, usually working over the real numbers. Over the real numbers, there are two such Jordan algebras up to
Up to
In mathematics, the phrase "up to x" means "disregarding a possible difference in x".For instance, when calculating an indefinite integral, one could say that the solution is f "up to addition by a constant," meaning it differs from f, if at all, only by some constant.It indicates that...
isomorphism
Isomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
. One of them, which was first mentioned by and studied by , is the set of 3×3 self-adjoint
Self-adjoint
In mathematics, an element x of a star-algebra is self-adjoint if x^*=x.A collection C of elements of a star-algebra is self-adjoint if it is closed under the involution operation...
matrices over the octonions, equipped with the binary operation
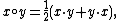
where
 denotes matrix multiplication. The other is defined the same way, but using split octonions instead of octonions.
denotes matrix multiplication. The other is defined the same way, but using split octonions instead of octonions.Over any algebraically closed field, there is just one Albert algebra. For example, if we complexify
Complexification
In mathematics, the complexification of a real vector space V is a vector space VC over the complex number field obtained by formally extending scalar multiplication to include multiplication by complex numbers. Any basis for V over the real numbers serves as a basis for VC over the complex...
the two Albert algebras over the real numbers, we obtain isomorphic Albert algebras over the complex numbers.
The Tits–Koecher construction applied to an Albert algebra gives a form of the E7 Lie algebra.

