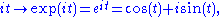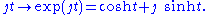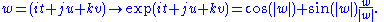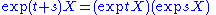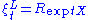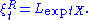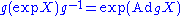
In differential geometry, the exponential map is a generalization of the ordinary exponential function

Exponential function

In mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...

 of mathematical analysis to all differentiable manifolds with an affine connection

Affine connection

In the branch of mathematics called differential geometry, an affine connection is a geometrical object on a smooth manifold which connects nearby tangent spaces, and so permits tangent vector fields to be differentiated as if they were functions on the manifold with values in a fixed vector space...

.
Two important special cases of this are the exponential map for a manifold with a Riemannian metric, and the exponential map from a Lie algebra

Lie algebra

In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...

 to a Lie group

Lie group

In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...

.

Definition

Let M be a differentiable manifold

Differentiable manifold

A differentiable manifold is a type of manifold that is locally similar enough to a linear space to allow one to do calculus. Any manifold can be described by a collection of charts, also known as an atlas. One may then apply ideas from calculus while working within the individual charts, since...

 and p a point of M. An affine connection

Affine connection

In the branch of mathematics called differential geometry, an affine connection is a geometrical object on a smooth manifold which connects nearby tangent spaces, and so permits tangent vector fields to be differentiated as if they were functions on the manifold with values in a fixed vector space...

 on M allows one to define the notion of a geodesic

Geodesic

In mathematics, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a Riemannian metric, geodesics are defined to be the shortest path between points in the space...

 through the point p.

Let v ∈ T_pM be a tangent vector

Tangent vector

A tangent vector is a vector that is tangent to a curve or surface at a given point.Tangent vectors are described in the differential geometry of curves in the context of curves in Rn. More generally, tangent vectors are elements of a tangent space of a differentiable manifold....

 to the manifold at p. Then there is a unique geodesic

Geodesic

In mathematics, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a Riemannian metric, geodesics are defined to be the shortest path between points in the space...

 γ_v satisfying γ_v(0) = p with initial tangent vector γ′_v(0) = v. The corresponding exponential map is defined by exp_p(v) = γ_v(1). In general, the exponential map is only locally defined, that is, it only takes a small neighborhood of the origin at T_pM, to a neighborhood of p in the manifold. This is because it relies on the theorem on existence and uniqueness for ordinary differential equation

Ordinary differential equation

In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....

s which is local in nature. An affine connection is called complete if the exponential map is well-defined at every point of the tangent bundle

Tangent bundle

In differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...

.

Lie theory

In the theory of Lie group

Lie group

In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...

s the exponential map is a map from the Lie algebra

Lie algebra

In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...

 of a Lie group to the group which allows one to recapture the local group structure from the Lie algebra. The existence of the exponential map is one of the primary justifications for the study of Lie groups at the level of Lie algebras.

The ordinary exponential function

Exponential function

In mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...

 of mathematical analysis is a special case of the exponential map when G is the multiplicative group of non-zero real number

Real number

In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...

s (whose Lie algebra is the additive group of all real numbers). The exponential map of a Lie group satisfies many properties analogous to those of the ordinary exponential function, however, it also differs in many important respects.

Definitions

Let be a Lie group

Lie group

In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...

 and be its Lie algebra

Lie algebra

In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...

 (thought of as the tangent space

Tangent space

In mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....

 to the identity element

Identity element

In mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...

 of ). The exponential map is a map
which can be defined in several different ways as follows:

• It is the exponential map of a canonical left-invariant affine connection on G, such that parallel transport is given by left translation.
• It is the exponential map of a canonical right-invariant affine connection on G. This is usually different from the canonical left-invariant connection, but both connections have the same geodesics (orbits of 1-parameter subgroups acting by left or right multiplication) so give the same exponential map.
• It is given by 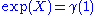where

is the unique one-parameter subgroup of whose tangent vector

Tangent vector

A tangent vector is a vector that is tangent to a curve or surface at a given point.Tangent vectors are described in the differential geometry of curves in the context of curves in Rn. More generally, tangent vectors are elements of a tangent space of a differentiable manifold....

 at the identity is equal to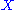 . It follows easily from the chain rule

Chain rule

In calculus, the chain rule is a formula for computing the derivative of the composition of two or more functions. That is, if f is a function and g is a function, then the chain rule expresses the derivative of the composite function in terms of the derivatives of f and g.In integration, the...

 that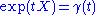 . The map 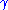may be constructed as the integral curve

Integral curve

In mathematics, an integral curve is a parametric curve that represents a specific solution to an ordinary differential equation or system of equations...

 of either the right- or left-invariant vector field

Vector field

In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...

 associated with . That the integral curve exists for all real parameters follows by right- or left-translating the solution near zero.

• If is a matrix Lie group, then the exponential map coincides with the matrix exponential
  Matrix exponential
  In mathematics, the matrix exponential is a matrix function on square matrices analogous to the ordinary exponential function. Abstractly, the matrix exponential gives the connection between a matrix Lie algebra and the corresponding Lie group....
  
   and is given by the ordinary series expansion:

.

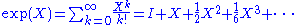• If G is compact, it has a Riemannian metric invariant under left and right translations, and the exponential map is the exponential map of this Riemannian metric.

Examples

• The unit circle
  Unit circle
  In mathematics, a unit circle is a circle with a radius of one. Frequently, especially in trigonometry, "the" unit circle is the circle of radius one centered at the origin in the Cartesian coordinate system in the Euclidean plane...
  
   centered at 0 in the complex plane
  Complex plane
  In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
  
   is a Lie group (called the circle group) whose tangent space at 1 can be identified with the imaginary line in the complex plane,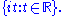 The exponential map for this Lie group is given by

  

that is, the same formula as the ordinary complex exponential.

• In the split-complex number
  Split-complex number
  In abstract algebra, the split-complex numbers are a two-dimensional commutative algebra over the real numbers different from the complex numbers. Every split-complex number has the formwhere x and y are real numbers...
  
   plane the imaginary line 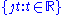forms the Lie algebra of the unit hyperbola
  Unit hyperbola
  In geometry, the unit hyperbola is the set of points in the Cartesian plane that satisfies x^2 - y^2 = 1 . In the study of indefinite orthogonal groups, the unit hyperbola forms the basis for an alternative radial lengthWhereas the unit circle surrounds its center, the unit hyperbola requires the...
  
   group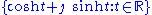 since the exponential map is given by

  

• The unit 3-sphere 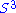centered at 0 in the quaternions H is a Lie group (isomorphic to the special unitary group 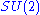) whose tangent space at 1 can be identified with the space of purely imaginary quaternions, 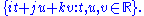The exponential map for this Lie group is given by

  

This map takes the 2-sphere of radius 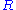inside the purely imaginary quaternions to 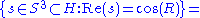a 2-sphere of radius 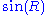when . Compare this to the first example above.

Properties

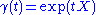• For all , the map is the unique one-parameter subgroup of whose tangent vector
  Tangent vector
  A tangent vector is a vector that is tangent to a curve or surface at a given point.Tangent vectors are described in the differential geometry of curves in the context of curves in Rn. More generally, tangent vectors are elements of a tangent space of a differentiable manifold....
  
   at the identity is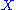 . It follows that:
  • 
  • 
• The exponential map is a smooth map. Its derivative at the identity, 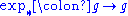, is the identity map (with the usual identifications). The exponential map, therefore, restricts to a diffeomorphism
  Diffeomorphism
  In mathematics, a diffeomorphism is an isomorphism in the category of smooth manifolds. It is an invertible function that maps one differentiable manifold to another, such that both the function and its inverse are smooth.- Definition :...
  
   from some neighborhood of 0 in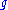 to a neighborhood of 1 in .
• The exponential map is not, however, a covering map
  Covering map
  In mathematics, more specifically algebraic topology, a covering map is a continuous surjective function p from a topological space, C, to a topological space, X, such that each point in X has a neighbourhood evenly covered by p...
  
   in general – it is not a local diffeomorphism at all points. For example, so(3) to SO(3) is not a covering map; see also cut locus
  Cut locus (Riemannian manifold)
  In Riemannian geometry, the cut locus of a point p in a manifold is roughly the set of all other points for which there are multiple minimizing geodesics connecting them from p, but it may contain additional points where the minimizing geodesic is unique, under certain circumstances...
  
   on this failure.
• The image of the exponential map always lies in the identity component
  Identity component
  In mathematics, the identity component of a topological group G is the connected component G0 of G that contains the identity element of the group...
  
   of . When is compact
  Compact space
  In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
  
  , the exponential map is surjective onto the identity component.
• The image of the exponential map of the connected but non-compact group SL₂(R) is not the whole group. Its image consists of C-diagonalizable matrices with eigenvalues either positive or with module 1, and of non-diagonalizable trigonalizable matrices with eigenvalue 1.
• The map is the integral curve
  Integral curve
  In mathematics, an integral curve is a parametric curve that represents a specific solution to an ordinary differential equation or system of equations...
  
   through the identity of both the right- and left-invariant vector fields associated to .
• The integral curve through 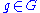of the left-invariant vector field 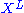associated to 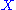is given by 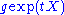. Likewise, the integral curve through 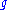of the right-invariant vector field 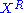is given by 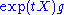. It follows that the flows 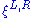generated by the vector fields 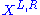are given by:
  • 
  • 
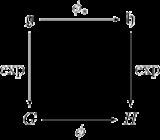
  Since these flows are globally defined, every left- and right-invariant vector field on is complete.
• Let 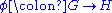be a Lie group homomorphism and let 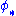be its derivative at the identity. Then the following diagram commutes
  Commutative diagram
  In mathematics, and especially in category theory, a commutative diagram is a diagram of objects and morphisms such that all directed paths in the diagram with the same start and endpoints lead to the same result by composition...
  
  :

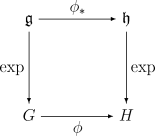
• In particular, when applied to the adjoint action of a group we have
  • 
  • 

Riemannian geometry

In Riemannian geometry

Riemannian geometry

Riemannian geometry is the branch of differential geometry that studies Riemannian manifolds, smooth manifolds with a Riemannian metric, i.e. with an inner product on the tangent space at each point which varies smoothly from point to point. This gives, in particular, local notions of angle, length...

, an exponential map is a map from a subset of a tangent space

Tangent space

In mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....

 T_pM of a Riemannian manifold

Riemannian manifold

In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...

 (or pseudo-Riemannian manifold

Pseudo-Riemannian manifold

In differential geometry, a pseudo-Riemannian manifold is a generalization of a Riemannian manifold. It is one of many mathematical objects named after Bernhard Riemann. The key difference between a Riemannian manifold and a pseudo-Riemannian manifold is that on a pseudo-Riemannian manifold the...

) M to M itself. The (pseudo) Riemannian metric determines a canonical affine connection, and the exponential map of the (pseudo) Riemannian manifold is given by the exponential map of this connection.

Properties

Intuitively speaking, the exponential map takes a given tangent vector to the manifold, runs along the geodesic starting at that point and going in that direction, for a unit time. Since v corresponds to the velocity vector of the geodesic, the actual (Riemannian) distance traveled will be dependent on that. We can also reparametrize geodesics to be unit speed, so equivalently we can define exp_p(v) = β(|v|) where β is the unit-speed geodesic (geodesic parameterized by arc length) going in the direction of v. As we vary the tangent vector v we will get, when applying exp_p, different points on M which are within some distance from the base point p—this is perhaps one of the most concrete ways of demonstrating that the tangent space to a manifold is a kind of "linearization" of the manifold.

The Hopf–Rinow theorem

Hopf–Rinow theorem

In mathematics, the Hopf–Rinow theorem is a set of statements about the geodesic completeness of Riemannian manifolds. It is named after Heinz Hopf and his student Willi Rinow .-Statement of the theorem:...

 asserts that it is possible to define the exponential map on the whole tangent space if and only if
the manifold is complete as a metric space

Metric space

In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...

 (which justifies the usual term geodesically complete for a manifold having an exponential map with this property). In particular, compact

Compact space

In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...

 manifolds are geodesically complete. However even if exp_p is defined on the whole tangent space, it will in general not be a global diffeomorphism. However, its differential at the origin of the tangent space is the identity map

Identity function

In mathematics, an identity function, also called identity map or identity transformation, is a function that always returns the same value that was used as its argument...

 and so, by the inverse function theorem

Inverse function theorem

In mathematics, specifically differential calculus, the inverse function theorem gives sufficient conditions for a function to be invertible in a neighborhood of a point in its domain...

 we can find a neighborhood of the origin of T_pM on which the exponential map is an embedding (i.e., the exponential map is a local diffeomorphism). The radius of the largest ball about the origin in T_pM that can be mapped diffeomorphically via exp_p is called the injectivity radius of M at p. The cut locus

Cut locus (Riemannian manifold)

In Riemannian geometry, the cut locus of a point p in a manifold is roughly the set of all other points for which there are multiple minimizing geodesics connecting them from p, but it may contain additional points where the minimizing geodesic is unique, under certain circumstances...

 of the exponential map is, roughly speaking, the set of all points where the exponential map fails to have a unique minimum.

An important property of the exponential map is the following lemma of Gauss

Gauss's lemma (Riemannian geometry)

In Riemannian geometry, Gauss's lemma asserts that any sufficiently small sphere centered at a point in a Riemannian manifold is perpendicular to every geodesic through the point. More formally, let M be a Riemannian manifold, equipped with its Levi-Civita connection, and p a point of M...

 (yet another Gauss's lemma

Gauss's lemma

Gauss's lemma can mean any of several lemmas named after Carl Friedrich Gauss:* Gauss's lemma * Gauss's lemma * Gauss's lemma...

): given any tangent vector v in the domain of definition of exp_p, and another vector w based at the tip of v (hence w is actually in the double-tangent space

Double tangent bundle

In mathematics, particularly differential topology, the double tangent bundle or the second tangent bundle refers to the tangent bundle of the total space TM of the tangent bundle of a smooth manifold M...

 T_v(T_pM)) and orthogonal to v, remains orthogonal to v when pushed forward via the exponential map. This means, in particular, that the boundary sphere of a small ball about the origin in T_pM is orthogonal to the geodesics in M determined by those vectors (i.e., the geodesics are radial). This motivates the definition of geodesic normal coordinates on a Riemannian manifold.

The exponential map is also useful in relating the abstract definition of curvature

Curvature of Riemannian manifolds

In mathematics, specifically differential geometry, the infinitesimal geometry of Riemannian manifolds with dimension at least 3 is too complicated to be described by a single number at a given point. Riemann introduced an abstract and rigorous way to define it, now known as the curvature tensor...

 to the more concrete realization of it originally conceived by Riemann himself—the sectional curvature

Sectional curvature

In Riemannian geometry, the sectional curvature is one of the ways to describe the curvature of Riemannian manifolds. The sectional curvature K depends on a two-dimensional plane σp in the tangent space at p...

 is intuitively defined as the Gaussian curvature

Gaussian curvature

In differential geometry, the Gaussian curvature or Gauss curvature of a point on a surface is the product of the principal curvatures, κ1 and κ2, of the given point. It is an intrinsic measure of curvature, i.e., its value depends only on how distances are measured on the surface, not on the way...

 of some surface (i.e., a slicing of the manifold by a 2-dimensional submanifold) through the point p in consideration. Via the exponential map, it now can be precisely defined as the Gaussian curvature of a surface through p determined by the image under exp_p of a 2-dimensional subspace of T_pM.

Relationships

In the case of Lie groups with a bi-invariant metric—a pseudo-Riemannian metric invariant under both left and right translation—the exponential maps of the pseudo-Riemannian structure are the same as the exponential maps of the Lie group. In general Lie groups do not have a bi-invariant metric, though all connected semisimple (or reductive) Lie groups do. The existence of a bi-invariant Riemannian metric is stronger than that of a pseudo-Riemannian metric, and implies that the Lie algebra is the Lie algebra of a compact Lie group; conversely, any compact (or abelian) Lie group has such a Riemannian metric.

Take the example that gives the "honest" exponential map. Consider the positive real numbers R⁺, a Lie group under the usual multiplication. Then each tangent space is just R. On each copy of R at the point y, we introduce the modified inner product
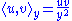
(multiplying them as usual real numbers but scaling by y²). (This is what makes the metric left-invariant, for left multiplication by a factor will just pull out of the inner product, twice — canceling the square in the denominator).

Consider the point 1 ∈ R⁺, and x ∈ R an element of the tangent space at 1. The usual straight line emanating from 1, namely y(t) = 1 + xt covers the same path as a geodesic, of course, except we have to reparametrize so as to get a curve with constant speed ("constant speed", remember, is not going to be the ordinary constant speed, because we're using this funny metric). To do this we reparametrize by arc length (the integral of the length of the tangent vector in the norm induced by the modified metric):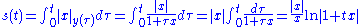


and after inverting the function to obtain t as a function of s, we substitute and get


Now using the unit speed definition, we have
,

giving the expected e^x.

The Riemannian distance defined by this is simply
,

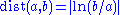a metric which should be familiar to anyone who has drawn graphs on log paper

Graph paper

Graph paper, graphing paper, grid paper or millimeter paper is writing paper that is printed with fine lines making up a regular grid. The lines are often used as guides for plotting mathematical functions or experimental data and drawing diagrams. It is commonly found in mathematics and...

.