Circle group

In mathematics

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, the circle group, denoted by T, is the multiplicative group

Group (mathematics)

In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...

 of all complex number

Complex number

A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...

s with absolute value 1, i.e., the unit circle

Unit circle

In mathematics, a unit circle is a circle with a radius of one. Frequently, especially in trigonometry, "the" unit circle is the circle of radius one centered at the origin in the Cartesian coordinate system in the Euclidean plane...

 in the complex plane

Complex plane

In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...

.
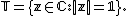
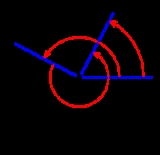
The circle group forms a subgroup

Subgroup

In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...

 of C^×, the multiplicative group of all nonzero complex numbers. Since C^× is abelian

Abelian group

In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...

, it follows that T is as well. The circle group is also the group U(1) of 1×1 unitary matrices; these act on the complex plane by rotation about the origin. The circle group can be parametrized by the angle θ of rotation by
This is the exponential map

Exponential map

In differential geometry, the exponential map is a generalization of the ordinary exponential function of mathematical analysis to all differentiable manifolds with an affine connection....

 for the circle group.

The circle group plays a central role in Pontryagin duality

Pontryagin duality

In mathematics, specifically in harmonic analysis and the theory of topological groups, Pontryagin duality explains the general properties of the Fourier transform on locally compact groups, such as R, the circle or finite cyclic groups.-Introduction:...

, and in the theory of Lie group

Lie group

In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...

s.

The notation T for the circle group stems from the fact that Tⁿ (the direct product

Direct product of groups

In the mathematical field of group theory, the direct product is an operation that takes two groups and and constructs a new group, usually denoted...

 of T with itself n times) is geometrically an n-torus

Torus

In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...

. The circle group is then a 1-torus.

Elementary introduction

One way to think about the circle group is that it describes how to add angles, where only angles between 0° and 360° are permitted. For example, the diagram illustrates how to add 150° to 270°. The answer should be 150° + 270° = 420°, but when thinking in terms of the circle group, we need to "forget" the fact that we have wrapped once around the circle. Therefore we adjust our answer by 360° which gives 420° = 60° (mod

Modular arithmetic

In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....

 360°).

Another description is in terms of ordinary addition, where only numbers between 0 and 1 are allowed (with 1 corresponding to a full rotation). To achieve this, we might need to throw away digits occurring before the decimal point. For example, when we work out 0.784 + 0.925 + 0.446, the answer should be 2.155, but we throw away the leading 2, so the answer (in the circle group) is just 0.155.

Topological and analytic structure

The circle group is more than just an abstract algebraic object. It has a natural topology when regarded as a subspace of the complex plane. Since multiplication and inversion are continuous functions on C^×, the circle group has the structure of a topological group

Topological group

In mathematics, a topological group is a group G together with a topology on G such that the group's binary operation and the group's inverse function are continuous functions with respect to the topology. A topological group is a mathematical object with both an algebraic structure and a...

. Moreover, since the unit circle is a closed subset of the complex plane, the circle group is a closed subgroup of C^× (itself regarded as a topological group).

One can say even more. The circle is a 1-dimensional real manifold

Manifold

In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....

 and multiplication and inversion are real-analytic maps

Analytic function

In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...

 on the circle. This gives the circle group the structure of a one-parameter group

One-parameter group

In mathematics, a one-parameter group or one-parameter subgroup usually means a continuous group homomorphismfrom the real line R to some other topological group G...

, an instance of a Lie group

Lie group

In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...

. In fact, up to

Up to

In mathematics, the phrase "up to x" means "disregarding a possible difference in  x".For instance, when calculating an indefinite integral, one could say that the solution is f "up to addition by a constant," meaning it differs from f, if at all, only by some constant.It indicates that...

 isomorphism, it is the unique 1-dimensional compact

Compact space

In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...

, connected

Connected space

In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...

 Lie group. Moreover, every n-dimensional compact, connected, abelian Lie group is isomorphic to Tⁿ.

Isomorphisms

The circle group shows up in a variety of forms in mathematics. We list some of the more common forms here. Specifically, we show that


Note that the slash (/) denotes here quotient group

Quotient group

In mathematics, specifically group theory, a quotient group is a group obtained by identifying together elements of a larger group using an equivalence relation...

.

The set of all 1×1 unitary matrices clearly coincides with the circle group; the unitary condition is equivalent to the condition that its element have absolute value 1. Therefore, the circle group is canonically isomorphic to U(1), the first unitary group

Unitary group

In mathematics, the unitary group of degree n, denoted U, is the group of n×n unitary matrices, with the group operation that of matrix multiplication. The unitary group is a subgroup of the general linear group GL...

.

The exponential function

Exponential function

In mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...

 gives rise to a group homomorphism

Group homomorphism

In mathematics, given two groups and , a group homomorphism from to is a function h : G → H such that for all u and v in G it holds that h = h \cdot h...

 exp : R → T from the additive real numbers R to the circle group T via the map


The last equality is Euler's formula

Euler's formula

Euler's formula, named after Leonhard Euler, is a mathematical formula in complex analysis that establishes the deep relationship between the trigonometric functions and the complex exponential function...

. The real number θ corresponds to the angle on the unit circle as measured from the positive x-axis. That this map is a homomorphism follows from the fact that the multiplication of unit complex numbers corresponds to addition of angles:


This exponential map is clearly a surjective function from R to T. It is not, however, injective. The kernel of this map is the set of all integer

Integer

The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...

 multiples of 2π. By the first isomorphism theorem we then have that


After rescaling we can also say that T is isomorphic to R/Z.

If complex numbers are realized as 2×2 real matrices

Matrix (mathematics)

In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...

 (see complex number

Complex number

A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...

), the unit complex numbers correspond to 2×2 orthogonal matrices with unit determinant

Determinant

In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...

. Specifically, we have


The circle group is therefore isomorphic to the special orthogonal group SO(2). This has the geometric interpretation that multiplication by a unit complex number is a proper rotation in the complex plane, and every such rotation is of this form.

Properties

Every compact Lie group G of dimension > 0 has a subgroup

Subgroup

In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...

 isomorphic to the circle group. That means that, thinking in terms of symmetry

Symmetry

Symmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...

, a compact symmetry group acting continuously can be expected to have one-parameter circle subgroups acting; the consequences in physical systems are seen for example at rotational invariance

Rotational invariance

In mathematics, a function defined on an inner product space is said to have rotational invariance if its value does not change when arbitrary rotations are applied to its argument...

, and spontaneous symmetry breaking

Spontaneous symmetry breaking

Spontaneous symmetry breaking is the process by which a system described in a theoretically symmetrical way ends up in an apparently asymmetric state....

.

The circle group has many subgroup

Subgroup

In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...

s, but its only proper closed

Closed set

In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...

 subgroups consist of roots of unity

Root of unity

In mathematics, a root of unity, or de Moivre number, is any complex number that equals 1 when raised to some integer power n. Roots of unity are used in many branches of mathematics, and are especially important in number theory, the theory of group characters, field theory, and the discrete...

: For each integer n > 0, the n^th roots of unity form a cyclic group

Cyclic group

In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...

 of order n, which is unique up to isomorphism.

Representations

The representations

Group representation

In the mathematical field of representation theory, group representations describe abstract groups in terms of linear transformations of vector spaces; in particular, they can be used to represent group elements as matrices so that the group operation can be represented by matrix multiplication...

 of the circle group are easy to describe. It follows from Schur's lemma

Schur's lemma

In mathematics, Schur's lemma is an elementary but extremely useful statement in representation theory of groups and algebras. In the group case it says that if M and N are two finite-dimensional irreducible representations...

 that the irreducible complex

Complex number

A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...

 representations of an abelian group are all 1-dimensional. Since the circle group is compact, any representation ρ : T → GL(1, C) ≅ C^×, must take values in U(1) ≅ T. Therefore, the irreducible representations of the circle group are just the homomorphisms from the circle group to itself. Every such homomorphism is of the form


These representations are all inequivalent. The representation φ_−n is conjugate to φ_n,


These representations are just the characters

Character (mathematics)

In mathematics, a character is a special kind of function from a group to a field . There are at least two distinct, but overlapping meanings...

 of the circle group. The character group

Character group

In mathematics, a character group is the group of representations of a group by complex-valued functions. These functions can be thought of as one-dimensional matrix representations and so are special cases of the group characters which arises in the related context of character theory...

 of T is clearly an infinite cyclic group generated by φ₁:


The irreducible real

Real number

In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...

 representations of the circle group are the trivial representation

Trivial representation

In the mathematical field of representation theory, a trivial representation is a representation of a group G on which all elements of G act as the identity mapping of V...

 (which is 1-dimensional) and the representations
taking values in SO(2). Here we only have positive integers n since the representation is equivalent to .

Group structure

In this section we will forget about the topological structure of the circle group and look only at its structure as an abstract group.

The circle group T is a divisible group

Divisible group

In mathematics, especially in the field of group theory, a divisible group is an abelian group in which every element can, in some sense, be divided by positive integers, or more accurately, every element is an nth multiple for each positive integer n...

. Its torsion subgroup

Torsion subgroup

In the theory of abelian groups, the torsion subgroup AT of an abelian group A is the subgroup of A consisting of all elements that have finite order...

 is given by the set of all nth roots of unity for all n, and is isomorphic to Q/Z. The structure theorem for divisible groups tells us that T is isomorphic to the direct sum of Q/Z with a number of copies of Q. The number of copies of Q must be c (the cardinality of the continuum

Cardinality of the continuum

In set theory, the cardinality of the continuum is the cardinality or “size” of the set of real numbers \mathbb R, sometimes called the continuum. It is an infinite cardinal number and is denoted by |\mathbb R| or \mathfrak c ....

) in order for the cardinality of the direct sum to be correct. But the direct sum of c copies of Q is isomorphic to R, as R is a vector space

Vector space

A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...

 of dimension c over Q. Thus


The isomorphism


can be proved in the same way, as C^× is also a divisible abelian group whose torsion subgroup is the same as the torsion subgroup of T.

See also

• Rotation number
  Rotation number
  In mathematics, the rotation number is an invariant of homeomorphisms of the circle. It was first defined by Henri Poincaré in 1885, in relation to the precession of the perihelion of a planetary orbit...
  
  
• Torus
  Torus
  In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
  
  
• One-parameter subgroup
• Unitary group
  Unitary group
  In mathematics, the unitary group of degree n, denoted U, is the group of n×n unitary matrices, with the group operation that of matrix multiplication. The unitary group is a subgroup of the general linear group GL...
  
  
• Orthogonal group
  Orthogonal group
  In mathematics, the orthogonal group of degree n over a field F is the group of n × n orthogonal matrices with entries from F, with the group operation of matrix multiplication...
  
  
• Group of rational points on the unit circle
  Group of rational points on the unit circle
  The rational points on the unit circle are those points such that both x and y are rational numbers and satisfy x2 + y2 = 1. The set of such points turns out to be closely related to primitive Pythagorean triples...