
Flow (mathematics)
Encyclopedia
In mathematics
, a flow formalizes the idea of the motion of particles in a fluid. Flows are ubiquitous in science, including engineering
and physics
. The notion of flow is basic to the study of ordinary differential equation
s. Informally, a flow may be viewed as a continuous motion of points over time. More formally, a flow is a group action
of the real number
s on a set.
The idea of a vector flow
, that is, the flow determined by a vector field
, occurs in the areas of differential topology
, Riemannian geometry
and Lie group
s. Specific examples of vector flows include the geodesic flow, the Hamiltonian flow, the Ricci flow
, the mean curvature flow
, and the Anosov flow.
of the additive group of real number
s on X. More explicitly, a flow is a mapping

such that, for all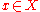 and all real numbers s and t:
and all real numbers s and t:
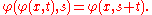
It is customary to write φt(x) instead of φ(x, t), so that the equations above can be expressed as and . Then for all the mapping is a bijection with inverse . This follows from the above definition, and the real parameter t may be taken as a generalized functional power, as in function iteration.
Flows are usually required to be compatible with structure
s furnished on the set X. In particular, if X is equipped with a topology
, then φ is usually required to be continuous
. If X is equipped with a differentiable structure
, then φ is usually required to be differentiable
. In these cases the flow forms a one parameter subgroup
of homeomorphisms and diffeomorphisms, respectively.
In certain situations one might also consider local flows, which are defined only in some subset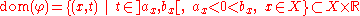
called the flow domain of φ. This is often the case with the flows of vector fields.
, physics
and the study of differential equation
s, to use a notation that makes the flow implicit. Thus, x(t) is written for φt(x), and one might say that the "variable x depends on the time t". Examples are given below.
In the case of a flow of a vector field V on a smooth manifold X, the flow is often denoted in such a way that its generator is made explicit. For example,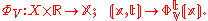
 is called the orbit of x under
is called the orbit of x under  Informally, it may be regarded as the trajectory of a particle
Informally, it may be regarded as the trajectory of a particle
that was initially positioned at x. If the flow is generated by a vector field
, then its orbits are the images of its integral curve
s.
and x:R→Rn the solution of the initial value problem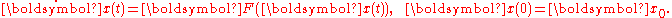
Then φ(x0,t)=x(t) is the flow of the vector field F. It is a well-defined local flow provided that the vector field F:Rn→Rn is Lipschitz-continuous. Then φ:Rn×R→Rn is also Lipschitz-continuous wherever defined. In general it may be hard to show that the flow φ is globally defined, but one simple criterion is that the vector field F is compactly supported.
x:R→Rn is the solution of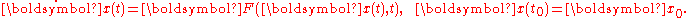
Then φt,t0(x_0,t,t0) is the time-dependent flow of F. It is not a "flow" by the definition above, but it can easily be seen as one by rearranging its arguments. Namely, the mapping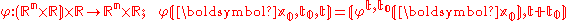
indeed satisfies the group law for the last variable: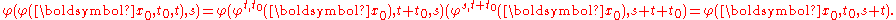
One can see time-dependent flows of vector fields as special cases of time-independent ones by the following trick. Define
Then y(t) is the solution of the "time-independent" initial value problem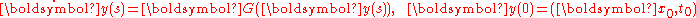
if and only if x(t) is the solution of the original time-dependent initial value problem. Furthermore, then the mapping φ is exactly the flow of the "time-independent" vector field G.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a flow formalizes the idea of the motion of particles in a fluid. Flows are ubiquitous in science, including engineering
Engineering
Engineering is the discipline, art, skill and profession of acquiring and applying scientific, mathematical, economic, social, and practical knowledge, in order to design and build structures, machines, devices, systems, materials and processes that safely realize improvements to the lives of...
and physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
. The notion of flow is basic to the study of ordinary differential equation
Ordinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
s. Informally, a flow may be viewed as a continuous motion of points over time. More formally, a flow is a group action
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
of the real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s on a set.
The idea of a vector flow
Vector flow
In mathematics, the vector flow refers to a set of closely related concepts of the flow determined by a vector field. These appear in a number of different contexts, including differential topology, Riemannian geometry and Lie group theory...
, that is, the flow determined by a vector field
Vector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
, occurs in the areas of differential topology
Differential topology
In mathematics, differential topology is the field dealing with differentiable functions on differentiable manifolds. It is closely related to differential geometry and together they make up the geometric theory of differentiable manifolds.- Description :...
, Riemannian geometry
Riemannian geometry
Riemannian geometry is the branch of differential geometry that studies Riemannian manifolds, smooth manifolds with a Riemannian metric, i.e. with an inner product on the tangent space at each point which varies smoothly from point to point. This gives, in particular, local notions of angle, length...
and Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
s. Specific examples of vector flows include the geodesic flow, the Hamiltonian flow, the Ricci flow
Ricci flow
In differential geometry, the Ricci flow is an intrinsic geometric flow. It is a process that deforms the metric of a Riemannian manifold in a way formally analogous to the diffusion of heat, smoothing out irregularities in the metric....
, the mean curvature flow
Mean curvature flow
In the field of differential geometry in mathematics, mean curvature flow is an example of a geometric flow of hypersurfaces in a Riemannian manifold . Intuitively, a family of surfaces evolves under mean curvature flow if the velocity of which a point on the surface moves is given by the mean...
, and the Anosov flow.
Formal definition
A flow on a set X is a group actionGroup action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
of the additive group of real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s on X. More explicitly, a flow is a mapping
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...

such that, for all
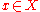 and all real numbers s and t:
and all real numbers s and t:
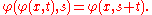
It is customary to write φt(x) instead of φ(x, t), so that the equations above can be expressed as and . Then for all the mapping is a bijection with inverse . This follows from the above definition, and the real parameter t may be taken as a generalized functional power, as in function iteration.
Flows are usually required to be compatible with structure
Mathematical structure
In mathematics, a structure on a set, or more generally a type, consists of additional mathematical objects that in some manner attach to the set, making it easier to visualize or work with, or endowing the collection with meaning or significance....
s furnished on the set X. In particular, if X is equipped with a topology
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
, then φ is usually required to be continuous
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
. If X is equipped with a differentiable structure
Differentiable manifold
A differentiable manifold is a type of manifold that is locally similar enough to a linear space to allow one to do calculus. Any manifold can be described by a collection of charts, also known as an atlas. One may then apply ideas from calculus while working within the individual charts, since...
, then φ is usually required to be differentiable
Differentiable function
In calculus , a differentiable function is a function whose derivative exists at each point in its domain. The graph of a differentiable function must have a non-vertical tangent line at each point in its domain...
. In these cases the flow forms a one parameter subgroup
One-parameter group
In mathematics, a one-parameter group or one-parameter subgroup usually means a continuous group homomorphismfrom the real line R to some other topological group G...
of homeomorphisms and diffeomorphisms, respectively.
In certain situations one might also consider local flows, which are defined only in some subset
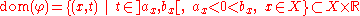
called the flow domain of φ. This is often the case with the flows of vector fields.
Alternative notations
It is very common in many fields, including engineeringEngineering
Engineering is the discipline, art, skill and profession of acquiring and applying scientific, mathematical, economic, social, and practical knowledge, in order to design and build structures, machines, devices, systems, materials and processes that safely realize improvements to the lives of...
, physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
and the study of differential equation
Differential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
s, to use a notation that makes the flow implicit. Thus, x(t) is written for φt(x), and one might say that the "variable x depends on the time t". Examples are given below.
In the case of a flow of a vector field V on a smooth manifold X, the flow is often denoted in such a way that its generator is made explicit. For example,
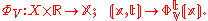
Orbits
Given x in X, the set is called the orbit of x under
is called the orbit of x under  Informally, it may be regarded as the trajectory of a particle
Informally, it may be regarded as the trajectory of a particlethat was initially positioned at x. If the flow is generated by a vector field
Vector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
, then its orbits are the images of its integral curve
Integral curve
In mathematics, an integral curve is a parametric curve that represents a specific solution to an ordinary differential equation or system of equations...
s.
Autonomous systems of ordinary differential equations
Let F:Rn→Rn be a (time-independent) vector fieldand x:R→Rn the solution of the initial value problem
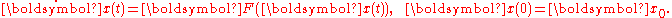
Then φ(x0,t)=x(t) is the flow of the vector field F. It is a well-defined local flow provided that the vector field F:Rn→Rn is Lipschitz-continuous. Then φ:Rn×R→Rn is also Lipschitz-continuous wherever defined. In general it may be hard to show that the flow φ is globally defined, but one simple criterion is that the vector field F is compactly supported.
Time-dependent ordinary differential equations
In the case of time-dependent vector fields F:Rn×R→Rn one denotes φt,t0(x0)=x(t), wherex:R→Rn is the solution of
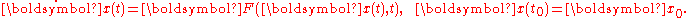
Then φt,t0(x_0,t,t0) is the time-dependent flow of F. It is not a "flow" by the definition above, but it can easily be seen as one by rearranging its arguments. Namely, the mapping
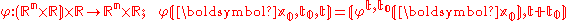
indeed satisfies the group law for the last variable:
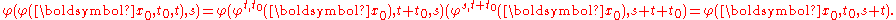
One can see time-dependent flows of vector fields as special cases of time-independent ones by the following trick. Define

Then y(t) is the solution of the "time-independent" initial value problem
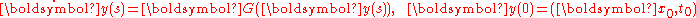
if and only if x(t) is the solution of the original time-dependent initial value problem. Furthermore, then the mapping φ is exactly the flow of the "time-independent" vector field G.

