Function field of an algebraic variety
Encyclopedia
In algebraic geometry
, the function field of an algebraic variety
V consists of objects which are interpreted as rational functions on V. In classical algebraic geometry
they are ratios of polynomials
; in complex algebraic geometry
these are meromorphic function
s and their higher-dimensional analogues; in modern algebraic geometry
they are elements of some quotient field.
, through which we may define meromorphic functions. The function field is then the set of all meromorphic functions on the variety. For the Riemann sphere
, which is the variety P1 over the complex numbers, the global meromorphic functions are exactly the rational function
s (that is, the ratios of complex polynomial functions). In any case, the meromorphic functions form a field, the function field.
coordinate chart, namely that consisting of the complex plane (all but the north pole of the sphere). On a general variety V, we say that a rational function on an open affine subset U is defined as the ratio of two polynomials in the affine coordinate ring of U, and that a rational function on all of V consists of such local data which agree on the intersections of open affines. We have defined the rational functions on V to be the field of fractions
of the affine coordinate ring of any open affine subset, since all such subsets are dense.
, then every open affine subset U is an integral domain and, hence, has a field of fractions. Furthermore, it can be verified that these are all the same, and are all equal to the local ring
of the generic point
of X. Thus the function field of X is just the local ring of its generic point. This point of view is developed further in function field (scheme theory)
.
is equal to the dimension
of the variety. All extensions of K that are finitely-generated as fields arise in this way from some algebraic variety.
Properties of the variety V that depend only on the function field are studied in birational geometry
.
The function field of the affine line over K is isomorphic to the field K(t) of rational function
s in one variable. This is also the function field of the projective line.
Consider the affine plane curve defined by the equation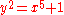
. Its function field is the field K(x,y), generated by transcendental elements satisfying the algebraic relation above.
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, the function field of an algebraic variety
Algebraic variety
In mathematics, an algebraic variety is the set of solutions of a system of polynomial equations. Algebraic varieties are one of the central objects of study in algebraic geometry...
V consists of objects which are interpreted as rational functions on V. In classical algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
they are ratios of polynomials
Rational function
In mathematics, a rational function is any function which can be written as the ratio of two polynomial functions. Neither the coefficients of the polynomials nor the values taken by the function are necessarily rational.-Definitions:...
; in complex algebraic geometry
Analytic variety
In mathematics, specifically geometry, an analytic variety is defined locally as the set of common zeros of finitely many analytic functions. It is analogous to the included concept of complex algebraic variety, and every complex manifold is an analytic variety. Since analytic varieties may have...
these are meromorphic function
Meromorphic function
In complex analysis, a meromorphic function on an open subset D of the complex plane is a function that is holomorphic on all D except a set of isolated points, which are poles for the function...
s and their higher-dimensional analogues; in modern algebraic geometry
Scheme (mathematics)
In mathematics, a scheme is an important concept connecting the fields of algebraic geometry, commutative algebra and number theory. Schemes were introduced by Alexander Grothendieck so as to broaden the notion of algebraic variety; some consider schemes to be the basic object of study of modern...
they are elements of some quotient field.
Definition for complex manifolds
More precisely, in complex algebraic geometry the objects of study are complex analytic varieties, on which we have a local notion of complex analysisComplex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
, through which we may define meromorphic functions. The function field is then the set of all meromorphic functions on the variety. For the Riemann sphere
Riemann sphere
In mathematics, the Riemann sphere , named after the 19th century mathematician Bernhard Riemann, is the sphere obtained from the complex plane by adding a point at infinity...
, which is the variety P1 over the complex numbers, the global meromorphic functions are exactly the rational function
Rational function
In mathematics, a rational function is any function which can be written as the ratio of two polynomial functions. Neither the coefficients of the polynomials nor the values taken by the function are necessarily rational.-Definitions:...
s (that is, the ratios of complex polynomial functions). In any case, the meromorphic functions form a field, the function field.
Construction in algebraic geometry
In classical algebraic geometry, we generalize the second point of view. For the Riemann sphere, above, the notion of a polynomial is not defined globally, but simply with respect to an affineAffine space
In mathematics, an affine space is a geometric structure that generalizes the affine properties of Euclidean space. In an affine space, one can subtract points to get vectors, or add a vector to a point to get another point, but one cannot add points. In particular, there is no distinguished point...
coordinate chart, namely that consisting of the complex plane (all but the north pole of the sphere). On a general variety V, we say that a rational function on an open affine subset U is defined as the ratio of two polynomials in the affine coordinate ring of U, and that a rational function on all of V consists of such local data which agree on the intersections of open affines. We have defined the rational functions on V to be the field of fractions
Field of fractions
In abstract algebra, the field of fractions or field of quotients of an integral domain is the smallest field in which it can be embedded. The elements of the field of fractions of the integral domain R have the form a/b with a and b in R and b ≠ 0...
of the affine coordinate ring of any open affine subset, since all such subsets are dense.
Generalization to arbitrary scheme
In the most general setting, that of modern scheme theory, we take the latter point of view above as a point of departure. Namely, if X is an integral schemeScheme (mathematics)
In mathematics, a scheme is an important concept connecting the fields of algebraic geometry, commutative algebra and number theory. Schemes were introduced by Alexander Grothendieck so as to broaden the notion of algebraic variety; some consider schemes to be the basic object of study of modern...
, then every open affine subset U is an integral domain and, hence, has a field of fractions. Furthermore, it can be verified that these are all the same, and are all equal to the local ring
Local ring
In abstract algebra, more particularly in ring theory, local rings are certain rings that are comparatively simple, and serve to describe what is called "local behaviour", in the sense of functions defined on varieties or manifolds, or of algebraic number fields examined at a particular place, or...
of the generic point
Generic point
In mathematics, in the fields general topology and particularly of algebraic geometry, a generic point P of a topological space X is an algebraic way of capturing the notion of a generic property: a generic property is a property of the generic point.- Definition and motivation :A generic point of...
of X. Thus the function field of X is just the local ring of its generic point. This point of view is developed further in function field (scheme theory)
Function field (scheme theory)
In algebraic geometry, the function field KX of a scheme Xis a generalization of the notion of a sheaf of rational functions on a variety. In the case of varieties, such a sheaf associates to each open set U the ring of all rational functions on that open set; in other words, KX is the set of...
.
Geometry of the function field
If V is a variety over a field K, then the function field K(V) is a field extension of the ground field K over which V is defined; its transcendence degreeTranscendence degree
In abstract algebra, the transcendence degree of a field extension L /K is a certain rather coarse measure of the "size" of the extension...
is equal to the dimension
Dimension of an algebraic variety
In mathematics, the dimension of an algebraic variety V in algebraic geometry is defined, informally speaking, as the number of independent rational functions that exist on V.For example, an algebraic curve has by definition dimension 1...
of the variety. All extensions of K that are finitely-generated as fields arise in this way from some algebraic variety.
Properties of the variety V that depend only on the function field are studied in birational geometry
Birational geometry
In mathematics, birational geometry is a part of the subject of algebraic geometry, that deals with the geometry of an algebraic variety that is dependent only on its function field. In the case of dimension two, the birational geometry of algebraic surfaces was largely worked out by the Italian...
.
Examples
The function field of a point over K is K.The function field of the affine line over K is isomorphic to the field K(t) of rational function
Rational function
In mathematics, a rational function is any function which can be written as the ratio of two polynomial functions. Neither the coefficients of the polynomials nor the values taken by the function are necessarily rational.-Definitions:...
s in one variable. This is also the function field of the projective line.
Consider the affine plane curve defined by the equation
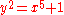. Its function field is the field K(x,y), generated by transcendental elements satisfying the algebraic relation above.