
Homogeneous coordinates
Encyclopedia
In mathematics
, homogeneous coordinates, introduced by August Ferdinand Möbius
in his 1827 work Der barycentrische Calcül, are a system of coordinates used in projective geometry
much as Cartesian coordinates
are used in Euclidean geometry
. They have the advantage that the coordinates of points, including points at infinity, can be represented using finite coordinates. Formulas involving homogeneous coordinates are often simpler and more symmetric than their Cartesian counterparts. Homogeneous coordinates have a range of applications, including computer graphics
and 3D computer vision
, where they allow affine transformation
s and, in general, projective transformations to be easily represented by a matrix.
If the homogeneous coordinates of a point are multiplied by a non-zero scalar then the resulting coordinates represent the same point. An additional condition must be added on the coordinates to ensure that only one set of coordinates corresponds to a given point, so the number of coordinates required is, in general, one more than the dimension of the projective space
being considered. For example, two homogeneous coordinates are required to specify a point on the projective line and three homogeneous coordinates are required to specify a point on the projective plane.
can be thought of as the Euclidean plane
with additional points, so called points at infinity, added. There is a point at infinity for each direction, informally defined as the limit of a point that moves in that direction away from a fixed point. Parallel lines in the Euclidean plane are said to intersect at a point at infinity corresponding to their common direction. A given point on the Euclidean plane is identified with two ratios , so the point corresponds to the triple where . Such a triple is a set of homogeneous coordinates for the point . Note that, since ratios are used, multiplying the three homogeneous coordinates by a common, non-zero factor does not change the point represented – unlike Cartesian coordinates, a single point can be represented by infinitely many homogeneous coordinates.
The equation of a line through the point may be written where l and m are not both 0. In parametric
form this can be written . Let Z=1/t, so the coordinates of a point on the line may be written . In homogeneous coordinates this becomes . In the limit as t approaches infinity, in other words as the point moves away from , Z becomes 0 and the homogeneous coordinates of the point become . So are defined as homogeneous coordinates of the point at infinity corresponding to the direction of the line .
To summarize:
Note that the triple is omitted and does not represent any point. The origin is represented by .
. Specifically, suppose there is a k such that
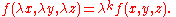
If a set of coordinates represent the same point as then it can be written for some non-zero value of λ. Then

A polynomial
of degree k can be turned into a homogeneous polynomial
by replacing x with x/z, y with y/z and multiplying by zk, in other words by defining

The resulting function f is a polynomial so it makes sense to extend its domain to triples where . The process can be reversed by setting , or

The equation can then be thought of as the homogeneous form of and it defines the same curve when restricted to the Euclidean plane. For example, the homogeneous form of the equation of the line is
may be represented by pairs of coordinates , not both zero. In this case, the point at infinity is . Similarly the points in projective n-space are represented by (n + 1)-tuples.
Lines in this space are defined to be sets of solutions of equations of the form where not all of a, b and c are zero. The condition depends only on the equivalence class of so the equation defines a set of points in the projective line. The mapping defines an inclusion from the Euclidean plane to the projective plane and the complement of the image is the set of points with z=0. This is the equation of a line according to the definition and the complement is called the line at infinity.
The equivalence classes, p, are the lines through the origin with the origin removed. The origin does not really play an essential part in the previous discussion so it can be added back in without changing the properties of the projective plane. This produces a variation on the definition, namely the projective plane is defined as the set of lines in R3 that pass through the origin and the coordinates of a non-zero element of a line are taken to be homogeneous coordinates of the line. These lines are now interpreted as points in the projective plane.
Again, this discussion applies analogously to other dimensions. So the projective space of dimension n can be defined as the set of lines through the origin in Rn+1.
as opposed to point coordinates. If in sx + ty + uz = 0 the letters s, t and u are taken as variables and x, y and z are taken as constants then equation becomes an equation of a set of lines in the space of all lines in the plane. Geometrically it represents the set of lines that pass though the point and may be interpreted as the equation of the point in line-coordinates. In the same way, planes in 3-space may be given sets of four homogeneous coordinates, and so on for higher dimensions.
, creates a set of six coordinate as the determinants from the homogeneous coordinates of two points and on the line. The Plücker embedding
is the generalization of this to create homogeneous coordinates of elements of any dimension m in a projective space of dimension n.
predicts that the number of points of intersection of two curves is equal to the product of their degrees (assuming an algebraically complete field and with certain conventions followed for counting intersection multiplicities). Bézout's theorem predicts there is one point of intersection of two lines and in general this is true, but when the lines are parallel the point of intersection is infinite. Homogeneous coordinates can be used to locate the point of intersection in this case. Similarly, Bézout's theorem predicts that a line will intersect a conic at two points, but in some cases one or both of the points is infinite and homogeneous coordinates must be used to locate them. For example, and have only one point of intersection in the finite plane. To find the other point of intersection, convert the equations into homogeneous form, and . This produces and, assuming not all of x, y and z are 0, the solutions are and . This first solution is the point in Cartesian coordinates, the finite point of intersection. The second solutions gives the homogeneous coordinates which corresponds to the direction of the y-axis. For the equations and there are no finite points of intersection. Converting the equations into homogeneous form gives and . Solving produces the equation which has a double root at . From the original equation, , so since at least one coordinate must be non-zero. Therefore is the point of intersection counted with multiplicity 2 in agreement with the theorem.
s.
A commonly known type of homogeneous coordinates are trilinear coordinates.
Let be the homogeneous coordinates of a point in the projective plane and for a fixed matrix
with , define a new set of coordinates by the equation
Multiplication of by a scalar results in the multiplication of by the same scalar, and X, Y and Z cannot be all 0 unless x, y and z are all zero since A is nonsingular. So are a new system of homogeneous coordinates for points in the projective plane. If z is fixed at 1 then
are proportional to the signed distances from the point to the lines
(The signed distance is the distance multiplied a sign 1 or −1 depending on which side of the line the point lies.) Note that for the value of X is simply a constant, and similarly for Y and Z.
The three lines,
in homogeneous coordinates, or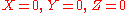
in the system, form a triangle called the triangle of reference for the system.
(or barycenter) of a system of three point masses placed at the vertices of a fixed triangle. Points within the triangle are represented by positive masses and points outside the triangle are represented by allowing negative masses. Multiplying the masses in the system by a scalar does not affect the center of mass, so this is a special case of a system of homogeneous coordinates.
, rotation
, scaling
and perspective projection to be implemented as matrix operations. Modern OpenGL
and DirectX
graphics cards take advantage of this to implement a vertex shader efficiently using vector processor
s with 4-element registers.
For example, in perspective projection a position in space is associated with the line from it to a fixed point called the center of projection. The point is then mapped to a plane by finding the point of intersection of that plane and the line. This produces an accurate representation of how a three dimensional object appears to the eye. In the simplest situation, the center of projection is the origin and points are mapped to the plane , working for the moment in Cartesian coordinates. For a given point in space, , the point where the line and the plane intersect is . Dropping the now superfluous z coordinate, this becomes . In homogeneous coordinates, the point is represented by and the point it maps to on the plane is represented by , so projection can be represented in matrix form as
Matrices representing other geometric transformations can be combined with this and each other by matrix multiplication. As a result, any perspective projection of space can be represented as a single matrix.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, homogeneous coordinates, introduced by August Ferdinand Möbius
August Ferdinand Möbius
August Ferdinand Möbius was a German mathematician and theoretical astronomer.He is best known for his discovery of the Möbius strip, a non-orientable two-dimensional surface with only one side when embedded in three-dimensional Euclidean space. It was independently discovered by Johann Benedict...
in his 1827 work Der barycentrische Calcül, are a system of coordinates used in projective geometry
Projective geometry
In mathematics, projective geometry is the study of geometric properties that are invariant under projective transformations. This means that, compared to elementary geometry, projective geometry has a different setting, projective space, and a selective set of basic geometric concepts...
much as Cartesian coordinates
Cartesian coordinate system
A Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...
are used in Euclidean geometry
Euclidean geometry
Euclidean geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions from these...
. They have the advantage that the coordinates of points, including points at infinity, can be represented using finite coordinates. Formulas involving homogeneous coordinates are often simpler and more symmetric than their Cartesian counterparts. Homogeneous coordinates have a range of applications, including computer graphics
Computer graphics
Computer graphics are graphics created using computers and, more generally, the representation and manipulation of image data by a computer with help from specialized software and hardware....
and 3D computer vision
Computer vision
Computer vision is a field that includes methods for acquiring, processing, analysing, and understanding images and, in general, high-dimensional data from the real world in order to produce numerical or symbolic information, e.g., in the forms of decisions...
, where they allow affine transformation
Affine transformation
In geometry, an affine transformation or affine map or an affinity is a transformation which preserves straight lines. It is the most general class of transformations with this property...
s and, in general, projective transformations to be easily represented by a matrix.
If the homogeneous coordinates of a point are multiplied by a non-zero scalar then the resulting coordinates represent the same point. An additional condition must be added on the coordinates to ensure that only one set of coordinates corresponds to a given point, so the number of coordinates required is, in general, one more than the dimension of the projective space
Projective space
In mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....
being considered. For example, two homogeneous coordinates are required to specify a point on the projective line and three homogeneous coordinates are required to specify a point on the projective plane.
Introduction
The projective planeProjective plane
In mathematics, a projective plane is a geometric structure that extends the concept of a plane. In the ordinary Euclidean plane, two lines typically intersect in a single point, but there are some pairs of lines that do not intersect...
can be thought of as the Euclidean plane
Euclidean geometry
Euclidean geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions from these...
with additional points, so called points at infinity, added. There is a point at infinity for each direction, informally defined as the limit of a point that moves in that direction away from a fixed point. Parallel lines in the Euclidean plane are said to intersect at a point at infinity corresponding to their common direction. A given point on the Euclidean plane is identified with two ratios , so the point corresponds to the triple where . Such a triple is a set of homogeneous coordinates for the point . Note that, since ratios are used, multiplying the three homogeneous coordinates by a common, non-zero factor does not change the point represented – unlike Cartesian coordinates, a single point can be represented by infinitely many homogeneous coordinates.
The equation of a line through the point may be written where l and m are not both 0. In parametric
Parametric equation
In mathematics, parametric equation is a method of defining a relation using parameters. A simple kinematic example is when one uses a time parameter to determine the position, velocity, and other information about a body in motion....
form this can be written . Let Z=1/t, so the coordinates of a point on the line may be written . In homogeneous coordinates this becomes . In the limit as t approaches infinity, in other words as the point moves away from , Z becomes 0 and the homogeneous coordinates of the point become . So are defined as homogeneous coordinates of the point at infinity corresponding to the direction of the line .
To summarize:
- Any point in the projective plane is represented by a triple , called the homogeneous coordinates of the point, where X, Y and Z are not all 0.
- The point represented by a given set of homogeneous coordinates is unchanged if the coordinates are multiplied by a common factor.
- Conversely, two sets of homogeneous coordinates represent the same point if and only if one is obtained from the other by multiplying by a common factor.
- When Z is not 0 the point represented is the point in the Euclidean plane.
- When Z is 0 the point represented is a point at infinity.
Note that the triple is omitted and does not represent any point. The origin is represented by .
Notation
Some authors use different notations for homogeneous coordinates which help distinguish them from Cartesian coordinates. The use of colons instead of commas, for example (x:y:z) instead of , emphasizes that the coordinates are to be considered ratios. Brackets, as in emphasize that multiple sets of coordinates are associated with a single point. Some authors use a combination of colons and brackets, as in [x:y:z].Homogeneity
Homogeneous coordinates are not uniquely determined by a point, so a function defined on the coordinates, say , does not determine a function defined on points as with Cartesian coordinates. But a condition defined on the coordinates, as might be used to describe a curve, determines a condition on points if the function is homogeneousHomogeneous function
In mathematics, a homogeneous function is a function with multiplicative scaling behaviour: if the argument is multiplied by a factor, then the result is multiplied by some power of this factor. More precisely, if is a function between two vector spaces over a field F, and k is an integer, then...
. Specifically, suppose there is a k such that
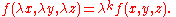
If a set of coordinates represent the same point as then it can be written for some non-zero value of λ. Then

A polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
of degree k can be turned into a homogeneous polynomial
Homogeneous polynomial
In mathematics, a homogeneous polynomial is a polynomial whose monomials with nonzero coefficients all have thesame total degree. For example, x^5 + 2 x^3 y^2 + 9 x y^4 is a homogeneous polynomial...
by replacing x with x/z, y with y/z and multiplying by zk, in other words by defining

The resulting function f is a polynomial so it makes sense to extend its domain to triples where . The process can be reversed by setting , or

The equation can then be thought of as the homogeneous form of and it defines the same curve when restricted to the Euclidean plane. For example, the homogeneous form of the equation of the line is
Other dimensions
The discussions in the preceding sections apply analogously to projective spaces other than the plane. So the points on the projective lineProjective line
In mathematics, a projective line is a one-dimensional projective space. The projective line over a field K, denoted P1, may be defined as the set of one-dimensional subspaces of the two-dimensional vector space K2 .For the generalisation to the projective line over an associative ring, see...
may be represented by pairs of coordinates , not both zero. In this case, the point at infinity is . Similarly the points in projective n-space are represented by (n + 1)-tuples.
Alternative definition
Another definition of projective space can be given in terms of equivalence classes. For non-zero element of R3, define to mean there is a non-zero λ so that . Then ~ is an equivalence relation and the projective plane can be defined as the equivalence classes of R3 − {0}. If is one of elements of the equivalence class p then these are taken to be homogeneous coordinates of p.Lines in this space are defined to be sets of solutions of equations of the form where not all of a, b and c are zero. The condition depends only on the equivalence class of so the equation defines a set of points in the projective line. The mapping defines an inclusion from the Euclidean plane to the projective plane and the complement of the image is the set of points with z=0. This is the equation of a line according to the definition and the complement is called the line at infinity.
The equivalence classes, p, are the lines through the origin with the origin removed. The origin does not really play an essential part in the previous discussion so it can be added back in without changing the properties of the projective plane. This produces a variation on the definition, namely the projective plane is defined as the set of lines in R3 that pass through the origin and the coordinates of a non-zero element of a line are taken to be homogeneous coordinates of the line. These lines are now interpreted as points in the projective plane.
Again, this discussion applies analogously to other dimensions. So the projective space of dimension n can be defined as the set of lines through the origin in Rn+1.
Elements other than points
The equation of a line in the projective plane may be given as where s, t and u are constants. Each triple determines a line, the line determined is unchanged if it is multiplied by a nonzero scalar, and at least one of s, t and u must be non-zero. So the triple may be taken to be homogeneous coordinates of a line in the projective plane, that is line coordinatesLine coordinates
In geometry, line coordinates are used to specify the position of a line just as point coordinates are used to specify the position of a point.-Lines in the plane:...
as opposed to point coordinates. If in sx + ty + uz = 0 the letters s, t and u are taken as variables and x, y and z are taken as constants then equation becomes an equation of a set of lines in the space of all lines in the plane. Geometrically it represents the set of lines that pass though the point and may be interpreted as the equation of the point in line-coordinates. In the same way, planes in 3-space may be given sets of four homogeneous coordinates, and so on for higher dimensions.
Duality
The same relation, , may be regarded either the equation of a line or the equation of a point. In general, there is no difference either algebraically or logically between the homogeneous coordinates of points and lines. So plane geometry with points as the fundamental elements and plane geometry with lines as the fundamental elements are equivalent except for interpretation. This leads to the concept of duality in projective geometry, the principle that the roles of points and lines can be interchanged in a theorem in projective geometry and the result will also be a theorem. Analogously, the theory of points in projective 3-space is dual to the theory of planes in projective 3-space, and so on for higher dimensions.Plücker coordinates
Assigning coordinates to lines in projective 3-space is more complicated since it would seem that at total of 8 coordinates, either the coordinates of two points which lie on the line or two planes whose intersection is the line. A useful method, due to Julius PlückerJulius Plücker
Julius Plücker was a German mathematician and physicist. He made fundamental contributions to the field of analytical geometry and was a pioneer in the investigations of cathode rays that led eventually to the discovery of the electron. He also vastly extended the study of Lamé curves.- Early...
, creates a set of six coordinate as the determinants from the homogeneous coordinates of two points and on the line. The Plücker embedding
Plücker embedding
In mathematics, the Plücker embedding describes a method to realize the Grassmannian of all r-dimensional subspaces of a vector space V as a subvariety of the projective space of the rth exterior power of that vector space, P....
is the generalization of this to create homogeneous coordinates of elements of any dimension m in a projective space of dimension n.
Application to Bézout's theorem
Bézout's theoremBézout's theorem
Bézout's theorem is a statement in algebraic geometry concerning the number of common points, or intersection points, of two plane algebraic curves. The theorem claims that the number of common points of two such curves X and Y is equal to the product of their degrees...
predicts that the number of points of intersection of two curves is equal to the product of their degrees (assuming an algebraically complete field and with certain conventions followed for counting intersection multiplicities). Bézout's theorem predicts there is one point of intersection of two lines and in general this is true, but when the lines are parallel the point of intersection is infinite. Homogeneous coordinates can be used to locate the point of intersection in this case. Similarly, Bézout's theorem predicts that a line will intersect a conic at two points, but in some cases one or both of the points is infinite and homogeneous coordinates must be used to locate them. For example, and have only one point of intersection in the finite plane. To find the other point of intersection, convert the equations into homogeneous form, and . This produces and, assuming not all of x, y and z are 0, the solutions are and . This first solution is the point in Cartesian coordinates, the finite point of intersection. The second solutions gives the homogeneous coordinates which corresponds to the direction of the y-axis. For the equations and there are no finite points of intersection. Converting the equations into homogeneous form gives and . Solving produces the equation which has a double root at . From the original equation, , so since at least one coordinate must be non-zero. Therefore is the point of intersection counted with multiplicity 2 in agreement with the theorem.
Circular points
The homogeneous form for the equation of a circle is . The intersection of this curve with the line at infinity can be found by setting . This produces the equation which has two solutions in the complex projective plane, and . These points are called the circular points at infinity and can be regarded as the common points of intersection of all circles. This can be generalized to curves of higher order as circular algebraic curveCircular algebraic curve
In geometry, a circular algebraic curve is a type of plane algebraic curve determined by an equation F = 0, where F is a polynomial with real coefficients and the highest-order terms of F form a polynomial divisible by x2 + y2...
s.
A commonly known type of homogeneous coordinates are trilinear coordinates.
Change of coordinate systems
Just as the selection of axes in the Cartesian coordinate is somewhat arbitrary, the selection of a single system of homogeneous coordinates out of all possible systems is somewhat arbitrary. Therefore it is useful to know how the different systems are related to each other.Let be the homogeneous coordinates of a point in the projective plane and for a fixed matrix

with , define a new set of coordinates by the equation

Multiplication of by a scalar results in the multiplication of by the same scalar, and X, Y and Z cannot be all 0 unless x, y and z are all zero since A is nonsingular. So are a new system of homogeneous coordinates for points in the projective plane. If z is fixed at 1 then

are proportional to the signed distances from the point to the lines

(The signed distance is the distance multiplied a sign 1 or −1 depending on which side of the line the point lies.) Note that for the value of X is simply a constant, and similarly for Y and Z.
The three lines,

in homogeneous coordinates, or
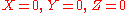
in the system, form a triangle called the triangle of reference for the system.
Barycentric coordinates
Möbius' original formulation of homogeneous coordinates specified the position of a point as the center of massCenter of mass
In physics, the center of mass or barycenter of a system is the average location of all of its mass. In the case of a rigid body, the position of the center of mass is fixed in relation to the body...
(or barycenter) of a system of three point masses placed at the vertices of a fixed triangle. Points within the triangle are represented by positive masses and points outside the triangle are represented by allowing negative masses. Multiplying the masses in the system by a scalar does not affect the center of mass, so this is a special case of a system of homogeneous coordinates.
Trilinear coordinates
Let l, m, n be three lines in the plane and define a set of coordinates X, Y and Z of a point p as the signed distances from p to these three lines. These are called the trilinear coordinates of p with respect to the triangle. Strictly speaking these are not homogeneous, since the values of X, Y and Z are determined exactly, not just up to proportionality. There is a linear relationship between them however, so these coordinates can be made homogeneous by allowing multiples of to represent the same point. More generally, X, Y and Z can be defined as constants p, r and q times the distances to l, m and n, resulting in a different system of homogeneous coordinates with the same triangle of reference. This is, in fact, the most general type of system of homogeneous coordinates for points in the plane if none of the lines is the line at infinity.Use in computer graphics
Homogeneous coordinates are ubiquitous in computer graphics because they allow common operations such as translationTranslation (geometry)
In Euclidean geometry, a translation moves every point a constant distance in a specified direction. A translation can be described as a rigid motion, other rigid motions include rotations and reflections. A translation can also be interpreted as the addition of a constant vector to every point, or...
, rotation
Rotation (mathematics)
In geometry and linear algebra, a rotation is a transformation in a plane or in space that describes the motion of a rigid body around a fixed point. A rotation is different from a translation, which has no fixed points, and from a reflection, which "flips" the bodies it is transforming...
, scaling
Scaling (geometry)
In Euclidean geometry, uniform scaling is a linear transformation that enlarges or shrinks objects by a scale factor that is the same in all directions. The result of uniform scaling is similar to the original...
and perspective projection to be implemented as matrix operations. Modern OpenGL
OpenGL
OpenGL is a standard specification defining a cross-language, cross-platform API for writing applications that produce 2D and 3D computer graphics. The interface consists of over 250 different function calls which can be used to draw complex three-dimensional scenes from simple primitives. OpenGL...
and DirectX
DirectX
Microsoft DirectX is a collection of application programming interfaces for handling tasks related to multimedia, especially game programming and video, on Microsoft platforms. Originally, the names of these APIs all began with Direct, such as Direct3D, DirectDraw, DirectMusic, DirectPlay,...
graphics cards take advantage of this to implement a vertex shader efficiently using vector processor
Vector processor
A vector processor, or array processor, is a central processing unit that implements an instruction set containing instructions that operate on one-dimensional arrays of data called vectors. This is in contrast to a scalar processor, whose instructions operate on single data items...
s with 4-element registers.
For example, in perspective projection a position in space is associated with the line from it to a fixed point called the center of projection. The point is then mapped to a plane by finding the point of intersection of that plane and the line. This produces an accurate representation of how a three dimensional object appears to the eye. In the simplest situation, the center of projection is the origin and points are mapped to the plane , working for the moment in Cartesian coordinates. For a given point in space, , the point where the line and the plane intersect is . Dropping the now superfluous z coordinate, this becomes . In homogeneous coordinates, the point is represented by and the point it maps to on the plane is represented by , so projection can be represented in matrix form as

Matrices representing other geometric transformations can be combined with this and each other by matrix multiplication. As a result, any perspective projection of space can be represented as a single matrix.
External links
- Jules Bloomenthal and Jon Rokne, Homogeneous coordinates http://www.unchainedgeometry.com/jbloom/pdf/homog-coords.pdf

