Examples

• This definition can be applied in particular to square matrices. The matrix

is nilpotent because A³ = 0. See nilpotent matrix

Nilpotent matrix

In linear algebra, a nilpotent matrix is a square matrix N such thatN^k = 0\,for some positive integer k. The smallest such k is sometimes called the degree of N....

 for more.

• In the factor ring Z/9Z, the equivalence class of 3 is nilpotent because 3² is congruent to 0 modulo
  Modular arithmetic
  In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
  
   9.

• Assume that two elements a, b in a (non-commutative) ring R satisfy ab = 0. Then the element c = ba is nilpotent (if non-zero) as c² = (ba)² = b(ab)a = 0. An example with matrices (for a, b):

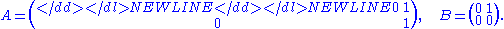
Here AB = 0, BA = B.

• The ring of coquaternion
  Coquaternion
  In abstract algebra, the split-quaternions or coquaternions are elements of a 4-dimensional associative algebra introduced by James Cockle in 1849 under the latter name. Like the quaternions introduced by Hamilton in 1843, they form a four dimensional real vector space equipped with a...
  
  s contains a cone
  Cone (linear algebra)
  In linear algebra, a cone is a subset of a vector space that is closed under multiplication by positive scalars. In other words, a subset C of a real vector space V is a cone if and only if λx belongs to C for any x in C and any positive scalar λ of V .A cone is said...
  
   of nilpotents.

Properties

No nilpotent element can be a unit

Unit (ring theory)

In mathematics, an invertible element or a unit in a ring R refers to any element u that has an inverse element in the multiplicative monoid of R, i.e. such element v that...

 (except in the trivial ring {0} which has only a single element 0 = 1). All non-zero nilpotent elements are zero divisor

Zero divisor

In abstract algebra, a nonzero element a of a ring is a left zero divisor if there exists a nonzero b such that ab = 0. Similarly, a nonzero element a of a ring is a right zero divisor if there exists a nonzero c such that ca = 0. An element that is both a left and a right zero divisor is simply...

s.

An n-by-n matrix A with entries from a field

Field (mathematics)

In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...

 is nilpotent if and only if its characteristic polynomial

Characteristic polynomial

In linear algebra, one associates a polynomial to every square matrix: its characteristic polynomial. This polynomial encodes several important properties of the matrix, most notably its eigenvalues, its determinant and its trace....

 is tⁿ.

The nilpotent elements from a commutative ring

Commutative ring

In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....

 form an ideal; this is a consequence of the binomial theorem

Binomial theorem

In elementary algebra, the binomial theorem describes the algebraic expansion of powers of a binomial. According to the theorem, it is possible to expand the power n into a sum involving terms of the form axbyc, where the exponents b and c are nonnegative integers with , and the coefficient a of...

. This ideal is the nilradical of the ring. Every nilpotent element in a commutative ring is contained in every prime ideal

Prime ideal

In algebra , a prime ideal is a subset of a ring which shares many important properties of a prime number in the ring of integers...

 of that ring, and in fact the intersection of all these prime ideals is equal to the nilradical.

If x is nilpotent, then 1 − x is a unit, because xⁿ = 0 entails
Further, if x is nilpotent, then 1 + x is also a unit.

Nilpotency in physics

An operand

Operand

In mathematics, an operand is the object of a mathematical operation, a quantity on which an operation is performed.-Example :The following arithmetic expression shows an example of operators and operands:3 + 6 = 9\;...

 Q that satisfies Q² = 0 is nilpotent. Grassmann number

Grassmann number

In mathematical physics, a Grassmann number, named after Hermann Grassmann, is a mathematical construction which allows a path integral representation for Fermionic fields...

s which allow a path integral

Path integral formulation

The path integral formulation of quantum mechanics is a description of quantum theory which generalizes the action principle of classical mechanics...

 representation for Fermionic fields are nilpotents since their squares vanish. The BRST charge is an important example in physics

Physics

Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...

.
As linear operators form an associative algebra and thus a ring, this is a special case of the initial definition. More generally, in view of the above definitions, an operator Q is nilpotent if there is n∈N such that Qⁿ = 0 (the zero function). Thus, a linear map is nilpotent iff

IFF

IFF, Iff or iff may refer to:Technology/Science:* Identification friend or foe, an electronic radio-based identification system using transponders...

 it has a nilpotent matrix in some basis. Another example for this is the exterior derivative

Exterior derivative

In differential geometry, the exterior derivative extends the concept of the differential of a function, which is a 1-form, to differential forms of higher degree. Its current form was invented by Élie Cartan....

 (again with n = 2). Both are linked, also through supersymmetry

Supersymmetry

In particle physics, supersymmetry is a symmetry that relates elementary particles of one spin to other particles that differ by half a unit of spin and are known as superpartners...

 and Morse theory

Morse theory

In differential topology, the techniques of Morse theory give a very direct way of analyzing the topology of a manifold by studying differentiable functions on that manifold. According to the basic insights of Marston Morse, a differentiable function on a manifold will, in a typical case, reflect...

, as shown by Edward Witten

Edward Witten

Edward Witten is an American theoretical physicist with a focus on mathematical physics who is currently a professor of Mathematical Physics at the Institute for Advanced Study....

 in a celebrated article.

The electromagnetic field

Electromagnetic field

An electromagnetic field is a physical field produced by moving electrically charged objects. It affects the behavior of charged objects in the vicinity of the field. The electromagnetic field extends indefinitely throughout space and describes the electromagnetic interaction...

 of a plane wave without sources is nilpotent when it is expressed in terms of the algebra of physical space

Algebra of physical space

In physics, the algebra of physical space is the use of the Clifford or geometric algebra Cℓ3 of the three-dimensional Euclidean space as a model for -dimensional space-time, representing a point in space-time via a paravector .The Clifford algebra Cℓ3 has a faithful representation, generated by...

.

Algebraic nilpotents

The two-dimensional dual number

Dual number

In linear algebra, the dual numbers extend the real numbers by adjoining one new element ε with the property ε2 = 0 . The collection of dual numbers forms a particular two-dimensional commutative unital associative algebra over the real numbers. Every dual number has the form z = a + bε with a and...

s contain a nilpotent basis element. Other algebras and numbers that contain nilpotent spaces include split-quaternions (coquaternions), split-octonion

Split-octonion

In mathematics, the split-octonions are a nonassociative extension of the quaternions . They differ from the octonions in the signature of quadratic form: the split-octonions have a split-signature whereas the octonions have a positive-definite signature .The split-octonions form the unique split...

s,
biquaternions , and complex octonions .

The source of this article is wikipedia, the free encyclopedia.  The text of this article is licensed under the GFDL.