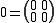Zero-product property - AbsoluteAstronomy.com

In the mathematical areas of algebra

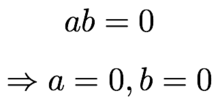
Abstract algebra

Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...

and analysis

Real analysis

Real analysis, is a branch of mathematical analysis dealing with the set of real numbers and functions of a real variable. In particular, it deals with the analytic properties of real functions and sequences, including convergence and limits of sequences of real numbers, the calculus of the real...

, the zero-product property, generally known as the nonexistence of zero divisor
Zero divisor
In abstract algebra, a nonzero element a of a ring is a left zero divisor if there exists a nonzero b such that ab = 0. Similarly, a nonzero element a of a ring is a right zero divisor if there exists a nonzero c such that ca = 0. An element that is both a left and a right zero divisor is simply...

s, and also called the zero-product rule, the rule of zero product, or any other similar name, is an abstract and explicit statement of the familiar property from elementary mathematics

Elementary mathematics

Elementary mathematics consists of mathematics topics frequently taught at the primary or secondary school levels. The most basic topics in elementary mathematics are arithmetic and geometry...

that if the product

Product (mathematics)

In mathematics, a product is the result of multiplying, or an expression that identifies factors to be multiplied. The order in which real or complex numbers are multiplied has no bearing on the product; this is known as the commutative law of multiplication...

of two real number

Real number

In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...

s is zero

0 (number)

0 is both a numberand the numerical digit used to represent that number in numerals.It fulfills a central role in mathematics as the additive identity of the integers, real numbers, and many other algebraic structures. As a digit, 0 is used as a placeholder in place value systems...

, then at least one of the numbers in the product (factors

Factorization

In mathematics, factorization or factoring is the decomposition of an object into a product of other objects, or factors, which when multiplied together give the original...

) must be zero.

The property is the defining characteristic of a type of commutative

Commutativity

In mathematics an operation is commutative if changing the order of the operands does not change the end result. It is a fundamental property of many binary operations, and many mathematical proofs depend on it...

ring

Ring (mathematics)

In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...

called an integral domain, in which no non-zero element is a zero divisor, or in the above terminology, every non-zero element possesses the zero-product rule.

Formal statement

A zero divisor is an element a of a ring that is not 0, but for which there exists another nonzero element b such that ab = 0. Thus, the zero-product property of a ring can be stated:

For all number
Number
A number is a mathematical object used to count and measure. In mathematics, the definition of number has been extended over the years to include such numbers as zero, negative numbers, rational numbers, irrational numbers, and complex numbers....

s a and b, ab = 0 implies a = 0 or b = 0 (or both).

The "zero-product property" of an element a of the ring is that a is not a zero divisor; explicitly:

For all nonzero b in the ring, ab is not 0.

Introduction

Elementary mathematics

Elementary mathematics consists of mathematics topics frequently taught at the primary or secondary school levels. The most basic topics in elementary mathematics are arithmetic and geometry...

includes the study of the sets of natural number

Natural number

In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...

s, the integer

Integer

The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...

s, the rational number

Rational number

In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...

s, and the real number

Real number

In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...

s. In each of these there is a number

Number

A number is a mathematical object used to count and measure. In mathematics, the definition of number has been extended over the years to include such numbers as zero, negative numbers, rational numbers, irrational numbers, and complex numbers....

(or element) zero

0 (number)

which has two properties:

that 0 multiplied
Multiplication
Multiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic ....

by any number a is 0: that is, 0 × a = 0 = a × 0 for any a in the set;
if the product
Product (mathematics)
In mathematics, a product is the result of multiplying, or an expression that identifies factors to be multiplied. The order in which real or complex numbers are multiplied has no bearing on the product; this is known as the commutative law of multiplication...

of two numbers a and b is 0 then one or both of a or b must be zero; otherwise stated, the product of two non-zero numbers is non-zero. Either of these is the zero-product property.

From Property 1 we derive the fact that, for example, 2 × 0 = 0. From Property 2 we know that if 2x = 0, where x is a real number, then we can be assured that x = 0. This is a result of the fact that the zero-product property holds for the real numbers (and also for all of its subsets).

Elementary examples

The zero-product property is used in solving elementary equation

Equation

An equation is a mathematical statement that asserts the equality of two expressions. In modern notation, this is written by placing the expressions on either side of an equals sign , for examplex + 3 = 5\,asserts that x+3 is equal to 5...

s in one variable

Variable (mathematics)

In mathematics, a variable is a value that may change within the scope of a given problem or set of operations. In contrast, a constant is a value that remains unchanged, though often unknown or undetermined. The concepts of constants and variables are fundamental to many areas of mathematics and...

In the solution of a linear equation
Linear equation
A linear equation is an algebraic equation in which each term is either a constant or the product of a constant and a single variable....

ax + b = 0 in the real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...

s, where a is non-zero, we factorize
Divisor
In mathematics, a divisor of an integer n, also called a factor of n, is an integer which divides n without leaving a remainder.-Explanation:...

by a to give a(x + b/a) = 0. By the zero-product property, since a is not zero, we conclude that x + b/a = 0, which implies that x = −b/a.

In higher-degree
Degree of a polynomial
The degree of a polynomial represents the highest degree of a polynominal's terms , should the polynomial be expressed in canonical form . The degree of an individual term is the sum of the exponents acting on the term's variables...

polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...

equation
Equation
An equation is a mathematical statement that asserts the equality of two expressions. In modern notation, this is written by placing the expressions on either side of an equals sign , for examplex + 3 = 5\,asserts that x+3 is equal to 5...

s the zero-product property may be invoked if the equation can be fully factored
Divisor
In mathematics, a divisor of an integer n, also called a factor of n, is an integer which divides n without leaving a remainder.-Explanation:...

. See Uses in analysis below.

The set of Natural Numbers generally starts with 1. A few authors also include 0 also in this set, however the set of natural numbers doesn't have 0.

Algebraic context

The study of algebra

Abstract algebra

Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...

involves consideration of sets of elements and operations

Operation (mathematics)

The general operation as explained on this page should not be confused with the more specific operators on vector spaces. For a notion in elementary mathematics, see arithmetic operation....

on them. There are often elements in a set which possess special properties. For example, if A is a group

Group (mathematics)

In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...

with operation +

Addition

Addition is a mathematical operation that represents combining collections of objects together into a larger collection. It is signified by the plus sign . For example, in the picture on the right, there are 3 + 2 apples—meaning three apples and two other apples—which is the same as five apples....

then there is a unique element 0 in A, called the additive identity

Additive identity

In mathematics the additive identity of a set which is equipped with the operation of addition is an element which, when added to any element x in the set, yields x...

, such that

0 + a = a = a + 0 for all a in A.

If the operation ×

Multiplication

Multiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic ....

of multiplication

Multiplication

Multiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic ....

is defined for A (such as in the mathematical object known as a ring

Ring (mathematics)

) then we can define an element 1 in A, called the multiplicative identity or unity, such that

1 × a = a = a × 1 for all a in A.

The interplay between the additive and multiplicative operations (where multiplication distributes

Distribution (mathematics)

In mathematical analysis, distributions are objects that generalize functions. Distributions make it possible to differentiate functions whose derivatives do not exist in the classical sense. In particular, any locally integrable function has a distributional derivative...

over addition) leads automatically to Property 1: that 0 × a = 0 = a × 0 for all a in A. This is true for any context in which addition and multiplication have group structures defined on the same set (for example, an algebra). Property 2 is, however, not a natural consequence of this interplay, as there are algebraic structures in which addition and multiplication are defined which do not have the zero-product property.

Proof of property 1:
a × 0 = a × ( b + (-b)) [by definition of additive inverse] = a × b + a × (-b) [by definition of distributivity] = a × b - a × b = 0

Examples

An integral domain is a ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...

in which, by definition, the zero-product property holds. Thus, for example, the zero-product property holds in the ring of integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...

s modulo
Modular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....

p,

Z_p = {0, 1, 2, ..., p − 1}

where p is a prime

Prime number

A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...

, the integer

Integer

The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...

s Z, the rational number

Rational number

s Q, the real number

Real number

In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...

s R, and the complex number

Complex number

A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...

s C since these are all integral domains.

Since any field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...

is an integral domain, the zero-product property holds in any field.

In the skew field of quaternions, the zero-product property holds. This ring is not an integral domain, because the multiplication is not commutative.

Any commutative ring
Commutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....

with the zero-product property is almost an integral domain (because it may not have unity); this deficiency is not critical, because the construction of the field of fractions
Field of fractions
In abstract algebra, the field of fractions or field of quotients of an integral domain is the smallest field in which it can be embedded. The elements of the field of fractions of the integral domain R have the form a/b with a and b in R and b ≠ 0...

works for this ring.

Examples of structures which do have zero divisors

It is not, however, true that the zero-product property necessarily holds in every structure which possesses an additive and multiplicative operation.

If a commutative ring R with unity is not an integral domain, then the zero-product property does not hold: that is, there are non-zero a and b in R such that ab = 0. For a specific example of this, if R is the ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...

of integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...

s modulo 6, or Z₆ = {0, 1, 2, 3, 4, 5} then there are 2, 3 in Z₆ such that 2 × 3 ≡ 0 (mod 6) but neither 2 ≡ 0 (mod 6) nor 3 ≡ 0 (mod 6).
In general, Z_n, where n is a composite number
Composite number
A composite number is a positive integer which has a positive divisor other than one or itself. In other words a composite number is any positive integer greater than one that is not a prime number....

, is not an integral domain and therefore the zero-product property does not hold. For if

n = m × q

with m, q < n, then neither m nor q is equal to 0 (mod n), but m × q = n = 0 (mod n), violating the zero-product property.

If R is the ring M₂(Z) of 2 by 2 matrices
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...

with integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...

coefficient
Coefficient
In mathematics, a coefficient is a multiplicative factor in some term of an expression ; it is usually a number, but in any case does not involve any variables of the expression...

s then there are matrices

and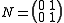

neither of which is equal to the zero matrix

such that

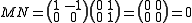so M₂(Z) does not possess the zero-product property.

The ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...

of all function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...

s f : [0, 1] → R, from the unit interval
Unit interval
In mathematics, the unit interval is the closed interval , that is, the set of all real numbers that are greater than or equal to 0 and less than or equal to 1...

to the real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...

s, has zero divisors: functions which are not identically equal to zero yet for which their product in the ring is the zero function. It is not hard to construct, for any n ≥ 2, n functions such that none is the zero function, but the product of any two is the zero function.

The same is true even if we consider only continuous functions, or only k-times differentiable functions.

Zero divisors

In a ring

Ring (mathematics)

R the elements for which the zero-product rule does not hold are called the zero divisor

Zero divisor

In abstract algebra, a nonzero element a of a ring is a left zero divisor if there exists a nonzero b such that ab = 0. Similarly, a nonzero element a of a ring is a right zero divisor if there exists a nonzero c such that ca = 0. An element that is both a left and a right zero divisor is simply...

s of the ring. The set of zero divisors, with 0 adjoined to it, may be denoted by Z(R). Thus Z(R) contains every element which can be multiplied

Multiplication

Multiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic ....

by some non-zero element to produce zero. In set notation

Set-builder notation

In set theory and its applications to logic, mathematics, and computer science, set-builder notation is a mathematical notation for describing a set by stating the properties that its members must satisfy...

Z(R) = {r in R | there is a non-zero s in R such that rs = 0 or sr = 0}.

Thus the number of zero divisors in a ring R is (by definition) a measure of how much the zero-product property fails to hold in R.

0 is not considered a zero divisor, because multiplication by 0 always results in a product equal to 0.

An integral domain has no zero divisors. The only element that, when multiplied by a nonzero element, can give product 0 is 0 itself. That is, Z(R) = {0}.

Uses in analysis

The zero-product property is used in solving polynomial

Polynomial

In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...

equations over the real number

Real number

In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...

s, such as quadratic equation

Quadratic equation

In mathematics, a quadratic equation is a univariate polynomial equation of the second degree. A general quadratic equation can be written in the formax^2+bx+c=0,\,...

For example, when finding all values of x which satisfy x² + x − 6 = 0, we first factor
Factorization
In mathematics, factorization or factoring is the decomposition of an object into a product of other objects, or factors, which when multiplied together give the original...

the left side of the equation to obtain (x + 3)(x − 2) = 0. Then, by the zero-product property, we know that either x + 3 = 0 (in which case x = − 3), or x − 2 = 0 (in which case x = 2). Thus, our solution is all x in the set {−3, 2}.

This method can be extended to polynomials of higher degree
Degree of a polynomial
The degree of a polynomial represents the highest degree of a polynominal's terms , should the polynomial be expressed in canonical form . The degree of an individual term is the sum of the exponents acting on the term's variables...

. In general, if a polynomial of degree n with coefficients in a ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...

R can be written as a product of factors (x − a₁)(x − a₂) ... (x − a_n) = 0 then the solution set is {a₁, a₂, ..., a_n}.

In the complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...

s the extension given above applies to any polynomial. Thus a polynomial f(z) of degree n over C can be written as a product of n factors (z − α) where α is one of precisely n roots of f. This is known as the fundamental theorem of algebra
Fundamental theorem of algebra
The fundamental theorem of algebra states that every non-constant single-variable polynomial with complex coefficients has at least one complex root...

.

Note that solving quadratic equations in algebraic structures in which the zero-product property does not hold can lead to surprising results. For example, the quadratic equation

x² − x = 0

has solutions {0, 1} in Z, Q, or R, but in Z₆ the solution set is {0, 1, 3, 4} since 3² − 3 = 6 ≡ 0 (mod 6) and 4² − 4 = 12 ≡ 0 (mod 6).

External links

PlanetMath: Zero rule of product

The source of this article is wikipedia, the free encyclopedia. The text of this article is licensed under the GFDL.

Formal statement

Introduction

Elementary examples

Algebraic context

Examples

Examples of structures which do have zero divisors

Zero divisors

Uses in analysis

See also

External links