Uniform polyhedron compound

A uniform polyhedron compound is a polyhedral compound

Polyhedral compound

A polyhedral compound is a polyhedron that is itself composed of several other polyhedra sharing a common centre. They are the three-dimensional analogs of polygonal compounds such as the hexagram....

 whose constituents are identical (although possibly enantiomorphous

Chirality

Chirality is a property of asymmetry important in several branches of science. It may refer to:* Chirality , a property of molecules having a non-superimposable mirror image...

) uniform polyhedra

Uniform polyhedron

A uniform polyhedron is a polyhedron which has regular polygons as faces and is vertex-transitive...

, in an arrangement that is also uniform: the symmetry group

Symmetry group

The symmetry group of an object is the group of all isometries under which it is invariant with composition as the operation...

 of the compound acts transitively on the compound's vertices.

The uniform polyhedron compounds were first enumerated by John Skilling in 1976, with a proof that the enumeration is complete. The following table lists them according to his numbering.

Compound	Bowers acronym	Picture	Polyhedral count	Polyhedral type Polyhedron In elementary geometry a polyhedron is a geometric solid in three dimensions with flat faces and straight edges...	Faces	Edges	Vertices	Notes	Symmetry group Symmetry group The symmetry group of an object is the group of all isometries under which it is invariant with composition as the operation...	Subgroup Subgroup In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H... restricting to one constituent
UC01 Compound of six tetrahedra with rotational freedom This uniform polyhedron compound is a symmetric arrangement of 6 tetrahedra, considered as antiprisms. It can be constructed by superimposing six tetrahedra within a cube, and then rotating them in pairs about the three axes that pass through the centres of two opposite cubic faces. Each...	sis		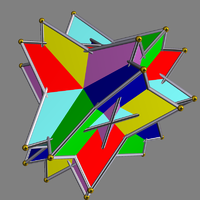6	tetrahedra Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...	24{3}	36	24	rotational freedom	Td Tetrahedral symmetry 150px|right|thumb|A regular [[tetrahedron]], an example of a solid with full tetrahedral symmetryA regular tetrahedron has 12 rotational symmetries, and a symmetry order of 24 including transformations that combine a reflection and a rotation.The group of all symmetries is isomorphic to the group...	S4 Cyclic symmetries This article deals with the four infinite series of point groups in three dimensions with n-fold rotational symmetry about one axis , and no other rotational symmetry :Chiral:*Cn of order n - n-fold rotational symmetry...
UC02 Compound of twelve tetrahedra with rotational freedom This uniform polyhedron compound is a symmetric arrangement of 12 tetrahedra, considered as antiprisms. It can be constructed by superimposing six identical copies of the stella octangula, and then rotating them in pairs about the three axes that pass through the centres of two opposite cubic...	dis		12	tetrahedra Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...	48{3}	72	48	rotational freedom	Oh Octahedral symmetry 150px|thumb|right|The [[cube]] is the most common shape with octahedral symmetryA regular octahedron has 24 rotational symmetries, and a symmetry order of 48 including transformations that combine a reflection and a rotation...	S4 Cyclic symmetries This article deals with the four infinite series of point groups in three dimensions with n-fold rotational symmetry about one axis , and no other rotational symmetry :Chiral:*Cn of order n - n-fold rotational symmetry...
UC03 Compound of six tetrahedra This uniform polyhedron compound is a symmetric arrangement of 6 tetrahedra. It can be constructed by inscribing a stella octangula within each cube in the compound of three cubes, or by stellating each octahedron in the compound of three octahedra....	snu		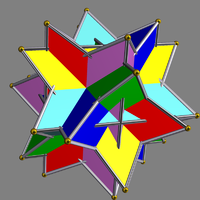6	tetrahedra Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...	24{3}	36	24		Oh Octahedral symmetry 150px|thumb|right|The [[cube]] is the most common shape with octahedral symmetryA regular octahedron has 24 rotational symmetries, and a symmetry order of 48 including transformations that combine a reflection and a rotation...	D2d Dihedral symmetry in three dimensions This article deals with three infinite sequences of point groups in three dimensions which have a symmetry group that as abstract group is a dihedral group Dihn .See also point groups in two dimensions.Chiral:...
UC04	so		2	tetrahedra Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...	8{3}	12	8	regular	Oh Octahedral symmetry 150px|thumb|right|The [[cube]] is the most common shape with octahedral symmetryA regular octahedron has 24 rotational symmetries, and a symmetry order of 48 including transformations that combine a reflection and a rotation...	Td Tetrahedral symmetry 150px|right|thumb|A regular [[tetrahedron]], an example of a solid with full tetrahedral symmetryA regular tetrahedron has 12 rotational symmetries, and a symmetry order of 24 including transformations that combine a reflection and a rotation.The group of all symmetries is isomorphic to the group...
UC05 Compound of five tetrahedra This compound polyhedron is also a stellation of the regular icosahedron. It was first described by Edmund Hess in 1876.-As a compound:It can be constructed by arranging five tetrahedra in rotational icosahedral symmetry , as colored in the upper right model...	ki		5	tetrahedra Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...	20{3}	30	20	regular	I Icosahedral symmetry A regular icosahedron has 60 rotational symmetries, and a symmetry order of 120 including transformations that combine a reflection and a rotation...	T Tetrahedral symmetry 150px|right|thumb|A regular [[tetrahedron]], an example of a solid with full tetrahedral symmetryA regular tetrahedron has 12 rotational symmetries, and a symmetry order of 24 including transformations that combine a reflection and a rotation.The group of all symmetries is isomorphic to the group...
UC06 Compound of ten tetrahedra This polyhedron can be seen as either a polyhedral stellation or a compound. This compound was first described by Edmund Hess in 1876.- As a compound :It can also be seen as the compound of ten tetrahedra with full icosahedral symmetry...	e		10	tetrahedra Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...	40{3}	60	20	regular 2 constituent polyhedra incident on each vertex	Ih Icosahedral symmetry A regular icosahedron has 60 rotational symmetries, and a symmetry order of 120 including transformations that combine a reflection and a rotation...	T Tetrahedral symmetry 150px|right|thumb|A regular [[tetrahedron]], an example of a solid with full tetrahedral symmetryA regular tetrahedron has 12 rotational symmetries, and a symmetry order of 24 including transformations that combine a reflection and a rotation.The group of all symmetries is isomorphic to the group...
UC07 Compound of six cubes with rotational freedom This uniform polyhedron compound is a symmetric arrangement of 6 cubes, considered as square prisms. It can be constructed by superimposing six identical cubes, and then rotating them in pairs about the three axes that pass through the centres of two opposite cubic faces. Each cube is rotated by an...	risdoh		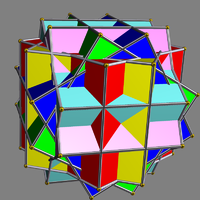6	cube Cube In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and... s	(12+24){4}	72	48	rotational freedom	Oh Octahedral symmetry 150px|thumb|right|The [[cube]] is the most common shape with octahedral symmetryA regular octahedron has 24 rotational symmetries, and a symmetry order of 48 including transformations that combine a reflection and a rotation...	C4h Cyclic symmetries This article deals with the four infinite series of point groups in three dimensions with n-fold rotational symmetry about one axis , and no other rotational symmetry :Chiral:*Cn of order n - n-fold rotational symmetry...
UC08 Compound of three cubes This uniform polyhedron compound is a symmetric arrangement of 3 cubes, considered as square prisms. It can be constructed by superimposing three identical cubes, and then rotating each by 45 degrees about a separate axis .This compound famously appears in the lithograph print Waterfall by M.C....	rah		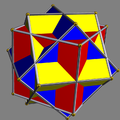3	cube Cube In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and... s	(6+12){4}	36	24		Oh Octahedral symmetry 150px|thumb|right|The [[cube]] is the most common shape with octahedral symmetryA regular octahedron has 24 rotational symmetries, and a symmetry order of 48 including transformations that combine a reflection and a rotation...	D4h Dihedral symmetry in three dimensions This article deals with three infinite sequences of point groups in three dimensions which have a symmetry group that as abstract group is a dihedral group Dihn .See also point groups in two dimensions.Chiral:...
UC09 Compound of five cubes This polyhedral compound is a symmetric arrangement of five cubes. This compound was first described by Edmund Hess in 1876.It is one of five regular compounds, and dual to the compound of five octahedra....	rhom		5	cube Cube In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and... s	30{4}	60	20	regular 2 constituent polyhedra incident on each vertex	Ih Icosahedral symmetry A regular icosahedron has 60 rotational symmetries, and a symmetry order of 120 including transformations that combine a reflection and a rotation...	Th Tetrahedral symmetry 150px|right|thumb|A regular [[tetrahedron]], an example of a solid with full tetrahedral symmetryA regular tetrahedron has 12 rotational symmetries, and a symmetry order of 24 including transformations that combine a reflection and a rotation.The group of all symmetries is isomorphic to the group...
UC10 Compound of four octahedra with rotational freedom This uniform polyhedron compound is a symmetric arrangement of 4 octahedra, considered as triangular antiprisms. It can be constructed by superimposing four identical octahedra, and then rotating each by an equal angle θ about a separate axis passing through the centres of two opposite octahedral...	dissit		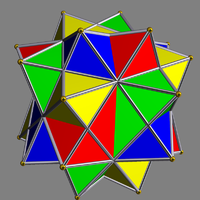4	octahedra Octahedron In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....	(8+24){3}	48	24	rotational freedom	Th Tetrahedral symmetry 150px|right|thumb|A regular [[tetrahedron]], an example of a solid with full tetrahedral symmetryA regular tetrahedron has 12 rotational symmetries, and a symmetry order of 24 including transformations that combine a reflection and a rotation.The group of all symmetries is isomorphic to the group...	S6 Cyclic symmetries This article deals with the four infinite series of point groups in three dimensions with n-fold rotational symmetry about one axis , and no other rotational symmetry :Chiral:*Cn of order n - n-fold rotational symmetry...
UC11 Compound of eight octahedra with rotational freedom This uniform polyhedron compound is a symmetric arrangement of 8 octahedra, considered as triangular antiprisms. It can be constructed by superimposing eight identical octahedra, and then rotating them in pairs about the four axes that pass through the centres of two opposite octahedral faces...	doso		8	octahedra Octahedron In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....	(16+48){3}	96	48	rotational freedom	Oh Octahedral symmetry 150px|thumb|right|The [[cube]] is the most common shape with octahedral symmetryA regular octahedron has 24 rotational symmetries, and a symmetry order of 48 including transformations that combine a reflection and a rotation...	S6 Cyclic symmetries This article deals with the four infinite series of point groups in three dimensions with n-fold rotational symmetry about one axis , and no other rotational symmetry :Chiral:*Cn of order n - n-fold rotational symmetry...
UC12 Compound of four octahedra This uniform polyhedron compound is a symmetric arrangement of 4 octahedra, considered as triangular antiprisms. It can be constructed by superimposing four identical octahedra, and then rotating each by 60 degrees about a separate axis .- Cartesian coordinates :Cartesian coordinates for the...	sno		4	octahedra Octahedron In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....	(8+24){3}	48	24		Oh Octahedral symmetry 150px|thumb|right|The [[cube]] is the most common shape with octahedral symmetryA regular octahedron has 24 rotational symmetries, and a symmetry order of 48 including transformations that combine a reflection and a rotation...	D3d Dihedral symmetry in three dimensions This article deals with three infinite sequences of point groups in three dimensions which have a symmetry group that as abstract group is a dihedral group Dihn .See also point groups in two dimensions.Chiral:...
UC13 Compound of twenty octahedra with rotational freedom This uniform polyhedron compound is a symmetric arrangement of 20 octahedra, considered as triangular antiprisms. It can be constructed by superimposing two copies of the compound of 10 octahedra UC16, and for each resulting pair of octahedra, rotating each octahedron in the pair by an equal and...	addasi		20	octahedra Octahedron In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....	(40+120){3}	240	120	rotational freedom	Ih Icosahedral symmetry A regular icosahedron has 60 rotational symmetries, and a symmetry order of 120 including transformations that combine a reflection and a rotation...	S6 Cyclic symmetries This article deals with the four infinite series of point groups in three dimensions with n-fold rotational symmetry about one axis , and no other rotational symmetry :Chiral:*Cn of order n - n-fold rotational symmetry...
UC14 Compound of twenty octahedra This uniform polyhedron compound is a symmetric arrangement of 20 octahedra . It is a special case of the compound of 20 octahedra with rotational freedom, in which pairs of octahedral vertices coincide.- Related polyhedra :...	dasi		20	octahedra Octahedron In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....	(40+120){3}	240	60	2 constituent polyhedra incident on each vertex	Ih Icosahedral symmetry A regular icosahedron has 60 rotational symmetries, and a symmetry order of 120 including transformations that combine a reflection and a rotation...	S6 Cyclic symmetries This article deals with the four infinite series of point groups in three dimensions with n-fold rotational symmetry about one axis , and no other rotational symmetry :Chiral:*Cn of order n - n-fold rotational symmetry...
UC15	gissi		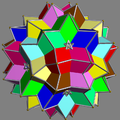10	octahedra Octahedron In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....	(20+60){3}	120	60		Ih Icosahedral symmetry A regular icosahedron has 60 rotational symmetries, and a symmetry order of 120 including transformations that combine a reflection and a rotation...	D3d Dihedral symmetry in three dimensions This article deals with three infinite sequences of point groups in three dimensions which have a symmetry group that as abstract group is a dihedral group Dihn .See also point groups in two dimensions.Chiral:...
UC16	si		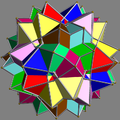10	octahedra Octahedron In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....	(20+60){3}	120	60		Ih Icosahedral symmetry A regular icosahedron has 60 rotational symmetries, and a symmetry order of 120 including transformations that combine a reflection and a rotation...	D3d Dihedral symmetry in three dimensions This article deals with three infinite sequences of point groups in three dimensions which have a symmetry group that as abstract group is a dihedral group Dihn .See also point groups in two dimensions.Chiral:...
UC17 Compound of five octahedra This polyhedron can be seen as either a polyhedral stellation or a compound. This compound was first described by Edmund Hess in 1876.- As a stellation :It is the second stellation of the icosahedron, and given as Wenninger model index 23....	se		5	octahedra Octahedron In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....	40{3}	60	30	regular	Ih Icosahedral symmetry A regular icosahedron has 60 rotational symmetries, and a symmetry order of 120 including transformations that combine a reflection and a rotation...	Th Tetrahedral symmetry 150px|right|thumb|A regular [[tetrahedron]], an example of a solid with full tetrahedral symmetryA regular tetrahedron has 12 rotational symmetries, and a symmetry order of 24 including transformations that combine a reflection and a rotation.The group of all symmetries is isomorphic to the group...
UC18 Compound of five tetrahemihexahedra A compound of five tetrahemihexahedra is a uniform polyhedron compound and a symmetric arrangement of five tetrahemihexahedra. It is chiral with icosahedral symmetry .- Related polyhedra :...	hirki		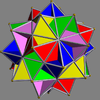5	tetrahemihexahedra Tetrahemihexahedron In geometry, the tetrahemihexahedron or hemicuboctahedron is a uniform star polyhedron, indexed as U4. It has 6 vertices and 12 edges, and 7 faces: 4 triangular and 3 square. Its vertex figure is a crossed quadrilateral. It has Coxeter-Dynkin diagram of ....	20{3} 15{4}	60	30		I Icosahedral symmetry A regular icosahedron has 60 rotational symmetries, and a symmetry order of 120 including transformations that combine a reflection and a rotation...	T Tetrahedral symmetry 150px|right|thumb|A regular [[tetrahedron]], an example of a solid with full tetrahedral symmetryA regular tetrahedron has 12 rotational symmetries, and a symmetry order of 24 including transformations that combine a reflection and a rotation.The group of all symmetries is isomorphic to the group...
UC19 Compound of twenty tetrahemihexahedra This uniform polyhedron compound is a symmetric arrangement of 20 tetrahemihexahedra. It is chiral with icosahedral symmetry .John Skilling notes, in his enumeration of uniform compounds of uniform polyhedra, that this compound of 20 tetrahemihexahedra is unique in that it cannot be obtained by...	sapisseri		20	tetrahemihexahedra Tetrahemihexahedron In geometry, the tetrahemihexahedron or hemicuboctahedron is a uniform star polyhedron, indexed as U4. It has 6 vertices and 12 edges, and 7 faces: 4 triangular and 3 square. Its vertex figure is a crossed quadrilateral. It has Coxeter-Dynkin diagram of ....	(20+60){3} 60{4}	240	60	2 constituent polyhedra incident on each vertex	I Icosahedral symmetry A regular icosahedron has 60 rotational symmetries, and a symmetry order of 120 including transformations that combine a reflection and a rotation...	C3 Cyclic symmetries This article deals with the four infinite series of point groups in three dimensions with n-fold rotational symmetry about one axis , and no other rotational symmetry :Chiral:*Cn of order n - n-fold rotational symmetry...
UC20 Prismatic compound of prisms with rotational freedom Each member of this infinite family of uniform polyhedron compounds is a symmetric arrangement of prisms sharing a common axis of rotational symmetry...	-		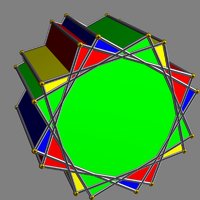2n (n>0)	p/q-gonal prisms Prismatic uniform polyhedron In geometry, a prismatic uniform polyhedron is a uniform polyhedron with dihedral symmetry. They exist in two infinite families, the uniform prisms and the uniform antiprisms...	4n{p/q} 2np{4}	6np	4np	rotational freedom gcd Greatest common divisor In mathematics, the greatest common divisor , also known as the greatest common factor , or highest common factor , of two or more non-zero integers, is the largest positive integer that divides the numbers without a remainder.For example, the GCD of 8 and 12 is 4.This notion can be extended to... (p,q)=1, p/q>2	Dnph Dihedral symmetry in three dimensions This article deals with three infinite sequences of point groups in three dimensions which have a symmetry group that as abstract group is a dihedral group Dihn .See also point groups in two dimensions.Chiral:...	Cph Cyclic symmetries This article deals with the four infinite series of point groups in three dimensions with n-fold rotational symmetry about one axis , and no other rotational symmetry :Chiral:*Cn of order n - n-fold rotational symmetry...
UC21 Prismatic compound of prisms Each member of this infinite family of uniform polyhedron compounds is a symmetric arrangement of prisms sharing a common axis of rotational symmetry.This infinite family can be enumerated as follows:...	-		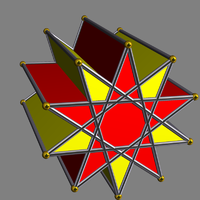n (n>1)	p/q-gonal prisms Prismatic uniform polyhedron In geometry, a prismatic uniform polyhedron is a uniform polyhedron with dihedral symmetry. They exist in two infinite families, the uniform prisms and the uniform antiprisms...	2n{p/q} np{4}	3np	2np	gcd Greatest common divisor In mathematics, the greatest common divisor , also known as the greatest common factor , or highest common factor , of two or more non-zero integers, is the largest positive integer that divides the numbers without a remainder.For example, the GCD of 8 and 12 is 4.This notion can be extended to... (p,q)=1, p/q>2	Dnph Dihedral symmetry in three dimensions This article deals with three infinite sequences of point groups in three dimensions which have a symmetry group that as abstract group is a dihedral group Dihn .See also point groups in two dimensions.Chiral:...	Dph Dihedral symmetry in three dimensions This article deals with three infinite sequences of point groups in three dimensions which have a symmetry group that as abstract group is a dihedral group Dihn .See also point groups in two dimensions.Chiral:...
UC22 Prismatic compound of antiprisms with rotational freedom Each member of this infinite family of uniform polyhedron compounds is a symmetric arrangement of antiprisms sharing a common axis of rotational symmetry...	-		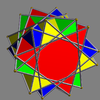2n (n>0)	p/q-gonal antiprisms Prismatic uniform polyhedron In geometry, a prismatic uniform polyhedron is a uniform polyhedron with dihedral symmetry. They exist in two infinite families, the uniform prisms and the uniform antiprisms...  (tetrahedra Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...  if p/q=2) (q odd)	4n{p/q} (unless p/q=2) 4np{3}	8np	4np	rotational freedom gcd Greatest common divisor In mathematics, the greatest common divisor , also known as the greatest common factor , or highest common factor , of two or more non-zero integers, is the largest positive integer that divides the numbers without a remainder.For example, the GCD of 8 and 12 is 4.This notion can be extended to... (p,q)=1, p/q>3/2	Dnpd Dihedral symmetry in three dimensions This article deals with three infinite sequences of point groups in three dimensions which have a symmetry group that as abstract group is a dihedral group Dihn .See also point groups in two dimensions.Chiral:...  (if n odd) Dnph Dihedral symmetry in three dimensions This article deals with three infinite sequences of point groups in three dimensions which have a symmetry group that as abstract group is a dihedral group Dihn .See also point groups in two dimensions.Chiral:...  (if n even)	S2p Cyclic symmetries This article deals with the four infinite series of point groups in three dimensions with n-fold rotational symmetry about one axis , and no other rotational symmetry :Chiral:*Cn of order n - n-fold rotational symmetry...
UC23 Prismatic compound of antiprisms Each member of this infinite family of uniform polyhedron compounds is a symmetric arrangement of antiprisms sharing a common axis of rotational symmetry.This infinite family can be enumerated as follows:...	-		n (n>1)	p/q-gonal antiprisms Prismatic uniform polyhedron In geometry, a prismatic uniform polyhedron is a uniform polyhedron with dihedral symmetry. They exist in two infinite families, the uniform prisms and the uniform antiprisms...  (tetrahedra Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...  if p/q=2) (q odd)	2n{p/q} (unless p/q=2) 2np{3}	4np	2np	gcd Greatest common divisor In mathematics, the greatest common divisor , also known as the greatest common factor , or highest common factor , of two or more non-zero integers, is the largest positive integer that divides the numbers without a remainder.For example, the GCD of 8 and 12 is 4.This notion can be extended to... (p,q)=1, p/q>3/2	Dnpd Dihedral symmetry in three dimensions This article deals with three infinite sequences of point groups in three dimensions which have a symmetry group that as abstract group is a dihedral group Dihn .See also point groups in two dimensions.Chiral:...  (if n odd) Dnph Dihedral symmetry in three dimensions This article deals with three infinite sequences of point groups in three dimensions which have a symmetry group that as abstract group is a dihedral group Dihn .See also point groups in two dimensions.Chiral:...  (if n even)	Dpd Dihedral symmetry in three dimensions This article deals with three infinite sequences of point groups in three dimensions which have a symmetry group that as abstract group is a dihedral group Dihn .See also point groups in two dimensions.Chiral:...
UC24 Prismatic compound of antiprisms with rotational freedom Each member of this infinite family of uniform polyhedron compounds is a symmetric arrangement of antiprisms sharing a common axis of rotational symmetry...	-		2n (n>0)	p/q-gonal antiprisms Prismatic uniform polyhedron In geometry, a prismatic uniform polyhedron is a uniform polyhedron with dihedral symmetry. They exist in two infinite families, the uniform prisms and the uniform antiprisms... (q even)	4n{p/q} 4np{3}	8np	4np	rotational freedom gcd Greatest common divisor In mathematics, the greatest common divisor , also known as the greatest common factor , or highest common factor , of two or more non-zero integers, is the largest positive integer that divides the numbers without a remainder.For example, the GCD of 8 and 12 is 4.This notion can be extended to... (p,q)=1, p/q>3/2	Dnph Dihedral symmetry in three dimensions This article deals with three infinite sequences of point groups in three dimensions which have a symmetry group that as abstract group is a dihedral group Dihn .See also point groups in two dimensions.Chiral:...	Cph Cyclic symmetries This article deals with the four infinite series of point groups in three dimensions with n-fold rotational symmetry about one axis , and no other rotational symmetry :Chiral:*Cn of order n - n-fold rotational symmetry...
UC25 Prismatic compound of antiprisms Each member of this infinite family of uniform polyhedron compounds is a symmetric arrangement of antiprisms sharing a common axis of rotational symmetry.This infinite family can be enumerated as follows:...	-		n (n>1)	p/q-gonal antiprisms Prismatic uniform polyhedron In geometry, a prismatic uniform polyhedron is a uniform polyhedron with dihedral symmetry. They exist in two infinite families, the uniform prisms and the uniform antiprisms... (q even)	2n{p/q} 2np{3}	4np	2np	gcd Greatest common divisor In mathematics, the greatest common divisor , also known as the greatest common factor , or highest common factor , of two or more non-zero integers, is the largest positive integer that divides the numbers without a remainder.For example, the GCD of 8 and 12 is 4.This notion can be extended to... (p,q)=1, p/q>3/2	Dnph Dihedral symmetry in three dimensions This article deals with three infinite sequences of point groups in three dimensions which have a symmetry group that as abstract group is a dihedral group Dihn .See also point groups in two dimensions.Chiral:...	Dph Dihedral symmetry in three dimensions This article deals with three infinite sequences of point groups in three dimensions which have a symmetry group that as abstract group is a dihedral group Dihn .See also point groups in two dimensions.Chiral:...
UC26 Compound of twelve pentagonal antiprisms with rotational freedom This uniform polyhedron compound is a symmetric arrangement of 12 pentagonal antiprisms. It can be constructed by inscribing one pair of pentagonal antiprisms within an icosahedron, in each of the six possible ways, and then rotating each by an equal and opposite angle θ.When θ is 36 degrees, the...	gadsid		12	pentagonal antiprism Pentagonal antiprism In geometry, the pentagonal antiprism is the third in an infinite set of antiprisms formed by an even-numbered sequence of triangle sides closed by two polygon caps. It consists of two pentagons joined to each other by a ring of 10 triangles for a total of 12 faces... s	120{3} 24{5}	240	120	rotational freedom	Ih Icosahedral symmetry A regular icosahedron has 60 rotational symmetries, and a symmetry order of 120 including transformations that combine a reflection and a rotation...	S10 Cyclic symmetries This article deals with the four infinite series of point groups in three dimensions with n-fold rotational symmetry about one axis , and no other rotational symmetry :Chiral:*Cn of order n - n-fold rotational symmetry...
UC27 Compound of six pentagonal antiprisms This uniform polyhedron compound is a symmetric arrangement of 6 pentagonal antiprisms. It can be constructed by inscribing within an icosahedron one pentagonal antiprism in each of the six possible ways, and then rotating each by 36 degrees about its axis .It shares its vertex arrangement with the...	gassid		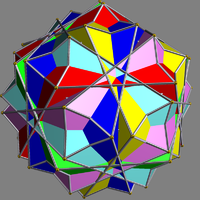6	pentagonal antiprism Pentagonal antiprism In geometry, the pentagonal antiprism is the third in an infinite set of antiprisms formed by an even-numbered sequence of triangle sides closed by two polygon caps. It consists of two pentagons joined to each other by a ring of 10 triangles for a total of 12 faces... s	60{3} 12{5}	120	60		Ih Icosahedral symmetry A regular icosahedron has 60 rotational symmetries, and a symmetry order of 120 including transformations that combine a reflection and a rotation...	D5d Dihedral symmetry in three dimensions This article deals with three infinite sequences of point groups in three dimensions which have a symmetry group that as abstract group is a dihedral group Dihn .See also point groups in two dimensions.Chiral:...
UC28 Compound of twelve pentagrammic crossed antiprisms with rotational freedom This uniform polyhedron compound is a symmetric arrangement of 12 pentagrammic crossed antiprisms. It can be constructed by inscribing one pair of pentagrammic crossed antiprisms within a great icosahedron, in each of the six possible ways, and then rotating each by an equal and opposite angle...	gidasid		12	pentagrammic crossed antiprisms	120{3} 24{5/2}	240	120	rotational freedom	Ih Icosahedral symmetry A regular icosahedron has 60 rotational symmetries, and a symmetry order of 120 including transformations that combine a reflection and a rotation...	S10 Cyclic symmetries This article deals with the four infinite series of point groups in three dimensions with n-fold rotational symmetry about one axis , and no other rotational symmetry :Chiral:*Cn of order n - n-fold rotational symmetry...
UC29 Compound of six pentagrammic crossed antiprisms This uniform polyhedron compound is a symmetric arrangement of 6 pentagrammic crossed antiprisms. It can be constructed by inscribing within a great icosahedron one pentagrammic crossed antiprism in each of the six possible ways, and then rotating each by 36 degrees about its axis...	gissed		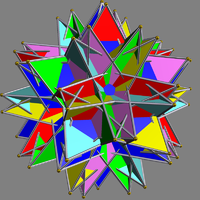6	pentagrammic crossed antiprisms	60{3} 12{5/2}	120	60		Ih Icosahedral symmetry A regular icosahedron has 60 rotational symmetries, and a symmetry order of 120 including transformations that combine a reflection and a rotation...	D5d Dihedral symmetry in three dimensions This article deals with three infinite sequences of point groups in three dimensions which have a symmetry group that as abstract group is a dihedral group Dihn .See also point groups in two dimensions.Chiral:...
UC30 Compound of four triangular prisms This uniform polyhedron compound is a chiral symmetric arrangement of 4 triangular prisms, aligned with the axes of three-fold rotational symmetry of an octahedron.- Cartesian coordinates :...	ro		4	triangular prism Triangular prism In geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides.... s	8{3} 12{4}	36	24		O Octahedral symmetry 150px|thumb|right|The [[cube]] is the most common shape with octahedral symmetryA regular octahedron has 24 rotational symmetries, and a symmetry order of 48 including transformations that combine a reflection and a rotation...	D3 Dihedral symmetry in three dimensions This article deals with three infinite sequences of point groups in three dimensions which have a symmetry group that as abstract group is a dihedral group Dihn .See also point groups in two dimensions.Chiral:...
UC31 Compound of eight triangular prisms This uniform polyhedron compound is a symmetric arrangement of 8 triangular prisms, aligned in pairs with the axes of three-fold rotational symmetry of an octahedron. It results from composing the two enantiomorphs of the compound of 4 triangular prisms....	dro		8	triangular prism Triangular prism In geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides.... s	16{3} 24{4}	72	48		Oh Octahedral symmetry 150px|thumb|right|The [[cube]] is the most common shape with octahedral symmetryA regular octahedron has 24 rotational symmetries, and a symmetry order of 48 including transformations that combine a reflection and a rotation...	D3 Dihedral symmetry in three dimensions This article deals with three infinite sequences of point groups in three dimensions which have a symmetry group that as abstract group is a dihedral group Dihn .See also point groups in two dimensions.Chiral:...
UC32 Compound of ten triangular prisms This uniform polyhedron compound is a chiral symmetric arrangement of 10 triangular prisms, aligned with the axes of three-fold rotational symmetry of an icosahedron.- Relatde polyhedra :...	kri		10	triangular prism Triangular prism In geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides.... s	20{3} 30{4}	90	60		I Icosahedral symmetry A regular icosahedron has 60 rotational symmetries, and a symmetry order of 120 including transformations that combine a reflection and a rotation...	D3 Dihedral symmetry in three dimensions This article deals with three infinite sequences of point groups in three dimensions which have a symmetry group that as abstract group is a dihedral group Dihn .See also point groups in two dimensions.Chiral:...
UC33 Compound of twenty triangular prisms This uniform polyhedron compound is a symmetric arrangement of 20 triangular prisms, aligned in pairs with the axes of three-fold rotational symmetry of an icosahedron.It results from composing the two enantiomorphs of the compound of 10 triangular prisms...	dri		20	triangular prism Triangular prism In geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides.... s	40{3} 60{4}	180	60	2 constituent polyhedra incident on each vertex	Ih Icosahedral symmetry A regular icosahedron has 60 rotational symmetries, and a symmetry order of 120 including transformations that combine a reflection and a rotation...	D3 Dihedral symmetry in three dimensions This article deals with three infinite sequences of point groups in three dimensions which have a symmetry group that as abstract group is a dihedral group Dihn .See also point groups in two dimensions.Chiral:...
UC34 Compound of six pentagonal prisms This uniform polyhedron compound is a chiral symmetric arrangement of 6 pentagonal prisms, aligned with the axes of fivefold rotational symmetry of a dodecahedron.- Related polyhedra :...	kred		6	pentagonal prism Pentagonal prism In geometry, the pentagonal prism is a prism with a pentagonal base. It is a type of heptahedron with 7 faces, 15 edges, and 10 vertices.- As a semiregular polyhedron :... s	30{4} 12{5}	90	60		I Icosahedral symmetry A regular icosahedron has 60 rotational symmetries, and a symmetry order of 120 including transformations that combine a reflection and a rotation...	D5 Dihedral symmetry in three dimensions This article deals with three infinite sequences of point groups in three dimensions which have a symmetry group that as abstract group is a dihedral group Dihn .See also point groups in two dimensions.Chiral:...
UC35 Compound of twelve pentagonal prisms This uniform polyhedron compound is a symmetric arrangement of 12 pentagonal prisms, aligned in pairs with the axes of fivefold rotational symmetry of a dodecahedron.It results from composing the two enantiomorphs of the compound of six pentagonal prisms...	dird		12	pentagonal prism Pentagonal prism In geometry, the pentagonal prism is a prism with a pentagonal base. It is a type of heptahedron with 7 faces, 15 edges, and 10 vertices.- As a semiregular polyhedron :... s	60{4} 24{5}	180	60	2 constituent polyhedra incident on each vertex	Ih Icosahedral symmetry A regular icosahedron has 60 rotational symmetries, and a symmetry order of 120 including transformations that combine a reflection and a rotation...	D5 Dihedral symmetry in three dimensions This article deals with three infinite sequences of point groups in three dimensions which have a symmetry group that as abstract group is a dihedral group Dihn .See also point groups in two dimensions.Chiral:...
UC36 Compound of six pentagrammic prisms This uniform polyhedron compound is a chiral symmetric arrangement of 6 pentagrammic prisms, aligned with the axes of fivefold rotational symmetry of a dodecahedron.- Related polyhedra :...	gikrid		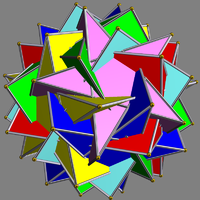6	pentagrammic prism Pentagrammic prism In geometry, the pentagrammic prism is one in an infinite set of nonconvex prisms formed by square sides and two regular star polygon caps, in this case two pentagrams.This polyhedron is identified with the indexed name U78 as a uniform polyhedron.... s	30{4} 12{5/2}	90	60		I Icosahedral symmetry A regular icosahedron has 60 rotational symmetries, and a symmetry order of 120 including transformations that combine a reflection and a rotation...	D5 Dihedral symmetry in three dimensions This article deals with three infinite sequences of point groups in three dimensions which have a symmetry group that as abstract group is a dihedral group Dihn .See also point groups in two dimensions.Chiral:...
UC37 Compound of twelve pentagrammic prisms This uniform polyhedron compound is a symmetric arrangement of 12 pentagrammic prisms, aligned in pairs with the axes of fivefold rotational symmetry of a dodecahedron.It results from composing the two enantiomorphs of the compound of six pentagrammic prisms...	giddird		12	pentagrammic prism Pentagrammic prism In geometry, the pentagrammic prism is one in an infinite set of nonconvex prisms formed by square sides and two regular star polygon caps, in this case two pentagrams.This polyhedron is identified with the indexed name U78 as a uniform polyhedron.... s	60{4} 24{5/2}	180	60	2 constituent polyhedra incident on each vertex	Ih Icosahedral symmetry A regular icosahedron has 60 rotational symmetries, and a symmetry order of 120 including transformations that combine a reflection and a rotation...	D5 Dihedral symmetry in three dimensions This article deals with three infinite sequences of point groups in three dimensions which have a symmetry group that as abstract group is a dihedral group Dihn .See also point groups in two dimensions.Chiral:...
UC38 Compound of four hexagonal prisms This uniform polyhedron compound is a symmetric arrangement of 4 hexagonal prisms, aligned with the axes of threefold rotational symmetry of an octahedron.- Cartesian coordinates :Cartesian coordinates for the vertices of this compound are all the permutations of...	griso		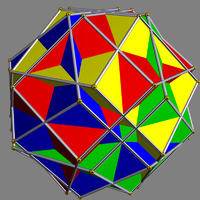4	hexagonal prism Hexagonal prism In geometry, the hexagonal prism is a prism with hexagonal base. The shape has 8 faces, 18 edges, and 12 vertices.Since it has eight faces, it is an octahedron. However, the term octahedron is primarily used to refer to the regular octahedron, which has eight triangular faces... s	24{4} 8{6}	72	48		Oh Octahedral symmetry 150px|thumb|right|The [[cube]] is the most common shape with octahedral symmetryA regular octahedron has 24 rotational symmetries, and a symmetry order of 48 including transformations that combine a reflection and a rotation...	D3d Dihedral symmetry in three dimensions This article deals with three infinite sequences of point groups in three dimensions which have a symmetry group that as abstract group is a dihedral group Dihn .See also point groups in two dimensions.Chiral:...
UC39 Compound of ten hexagonal prisms This uniform polyhedron compound is a symmetric arrangement of 10 hexagonal prisms, aligned with the axes of three-fold rotational symmetry of an icosahedron.- Cartesian coordinates :...	rosi		10	hexagonal prism Hexagonal prism In geometry, the hexagonal prism is a prism with hexagonal base. The shape has 8 faces, 18 edges, and 12 vertices.Since it has eight faces, it is an octahedron. However, the term octahedron is primarily used to refer to the regular octahedron, which has eight triangular faces... s	60{4} 20{6}	180	120		Ih Icosahedral symmetry A regular icosahedron has 60 rotational symmetries, and a symmetry order of 120 including transformations that combine a reflection and a rotation...	D3d Dihedral symmetry in three dimensions This article deals with three infinite sequences of point groups in three dimensions which have a symmetry group that as abstract group is a dihedral group Dihn .See also point groups in two dimensions.Chiral:...
UC40 Compound of six decagonal prisms This uniform polyhedron compound is a symmetric arrangement of 6 decagonal prisms, aligned with the axes of fivefold rotational symmetry of a dodecahedron.- Cartesian coordinates :...	rassid		6	decagonal prism Decagonal prism In geometry, the decagonal prism is the eighth in an infinite set of prisms, formed by ten square side faces and two regular decagon caps. With twelve faces, it is one of many nonregular dodecahedra.If faces are all regular, it is a semiregular polyhedron.... s	60{4} 12{10}	180	120		Ih Icosahedral symmetry A regular icosahedron has 60 rotational symmetries, and a symmetry order of 120 including transformations that combine a reflection and a rotation...	D5d Dihedral symmetry in three dimensions This article deals with three infinite sequences of point groups in three dimensions which have a symmetry group that as abstract group is a dihedral group Dihn .See also point groups in two dimensions.Chiral:...
UC41 Compound of six decagrammic prisms This uniform polyhedron compound is a symmetric arrangement of 6 decagrammic prisms, aligned with the axes of fivefold rotational symmetry of a dodecahedron.- Cartesian coordinates :...	grassid		6	decagrammic prism Decagrammic prism In geometry, the decagrammic prism is one of an infinite set of nonconvex prisms formed by squares sides and two regular star polygon caps, in this case two decagrams.... s	60{4} 12{10/3}	180	120		Ih Icosahedral symmetry A regular icosahedron has 60 rotational symmetries, and a symmetry order of 120 including transformations that combine a reflection and a rotation...	D5d Dihedral symmetry in three dimensions This article deals with three infinite sequences of point groups in three dimensions which have a symmetry group that as abstract group is a dihedral group Dihn .See also point groups in two dimensions.Chiral:...
UC42 Compound of three square antiprisms This uniform polyhedron compound is a symmetric arrangement of 3 square antiprisms, aligned with the three axes of 4-fold rotational symmetry of a cube.- Cartesian coordinates :...	gassic		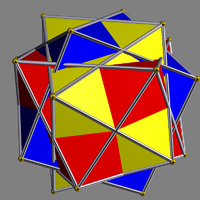3	square antiprism Square antiprism In geometry, the square antiprism is the second in an infinite set of antiprisms formed by an even-numbered sequence of triangle sides closed by two polygon caps... s	24{3} 6{4}	48	24		O Octahedral symmetry 150px|thumb|right|The [[cube]] is the most common shape with octahedral symmetryA regular octahedron has 24 rotational symmetries, and a symmetry order of 48 including transformations that combine a reflection and a rotation...	D4 Dihedral symmetry in three dimensions This article deals with three infinite sequences of point groups in three dimensions which have a symmetry group that as abstract group is a dihedral group Dihn .See also point groups in two dimensions.Chiral:...
UC43 Compound of six square antiprisms This uniform polyhedron compound is a symmetric arrangement of 6 square antiprisms, aligned in pairs with the three axes of 4-fold rotational symmetry of a cube. It results from composing the two enantiomers of the compound of 3 square antiprisms....	gidsac		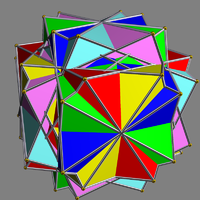6	square antiprism Square antiprism In geometry, the square antiprism is the second in an infinite set of antiprisms formed by an even-numbered sequence of triangle sides closed by two polygon caps... s	48{3} 12{4}	96	48		Oh Octahedral symmetry 150px|thumb|right|The [[cube]] is the most common shape with octahedral symmetryA regular octahedron has 24 rotational symmetries, and a symmetry order of 48 including transformations that combine a reflection and a rotation...	D4 Dihedral symmetry in three dimensions This article deals with three infinite sequences of point groups in three dimensions which have a symmetry group that as abstract group is a dihedral group Dihn .See also point groups in two dimensions.Chiral:...
UC44 Compound of six pentagrammic antiprisms This uniform polyhedron compound is a chiral symmetric arrangement of 6 pentagrammic antiprisms, aligned with the axes of fivefold rotational symmetry of a dodecahedron.- Cartesian coordinates :...	sassid		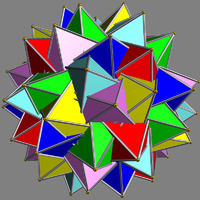6	pentagrammic antiprism Pentagrammic antiprism In geometry, the pentagrammic antiprism is one in an infinite set of nonconvex antiprisms formed by triangle sides and two regular star polygon caps, in this case two pentagrams.This polyhedron is identified with the indexed name U79 as a uniform polyhedron.... s	60{3} 12{5/2}	120	60		I Icosahedral symmetry A regular icosahedron has 60 rotational symmetries, and a symmetry order of 120 including transformations that combine a reflection and a rotation...	D5 Dihedral symmetry in three dimensions This article deals with three infinite sequences of point groups in three dimensions which have a symmetry group that as abstract group is a dihedral group Dihn .See also point groups in two dimensions.Chiral:...
UC45 Compound of twelve pentagrammic antiprisms This uniform polyhedron compound is a symmetric arrangement of 12 pentagrammic antiprisms, aligned in pairs with the axes of fivefold rotational symmetry of a dodecahedron. It results from composing the two enantiomorphs of the compound of 6 pentagrammic antiprisms....	sadsid		12	pentagrammic antiprism Pentagrammic antiprism In geometry, the pentagrammic antiprism is one in an infinite set of nonconvex antiprisms formed by triangle sides and two regular star polygon caps, in this case two pentagrams.This polyhedron is identified with the indexed name U79 as a uniform polyhedron.... s	120{3} 24{5/2}	240	120		Ih Icosahedral symmetry A regular icosahedron has 60 rotational symmetries, and a symmetry order of 120 including transformations that combine a reflection and a rotation...	D5 Dihedral symmetry in three dimensions This article deals with three infinite sequences of point groups in three dimensions which have a symmetry group that as abstract group is a dihedral group Dihn .See also point groups in two dimensions.Chiral:...
UC46 Compound of two icosahedra This uniform polyhedron compound is a composition of 2 icosahedra. It has octahedral symmetry Oh.The triangles in this compound decompose into two orbits under action of the symmetry group: 16 of the triangles lie in coplanar pairs in octahedral planes, while the other 24 lie in unique planes.It...	siddo		2	icosahedra Icosahedron In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids....	(16+24){3}	60	24		Oh Octahedral symmetry 150px|thumb|right|The [[cube]] is the most common shape with octahedral symmetryA regular octahedron has 24 rotational symmetries, and a symmetry order of 48 including transformations that combine a reflection and a rotation...	Th Tetrahedral symmetry 150px|right|thumb|A regular [[tetrahedron]], an example of a solid with full tetrahedral symmetryA regular tetrahedron has 12 rotational symmetries, and a symmetry order of 24 including transformations that combine a reflection and a rotation.The group of all symmetries is isomorphic to the group...
UC47 Compound of five icosahedra This uniform polyhedron compound is a composition of 5 icosahedra. It has icosahedral symmetry Ih.The triangles in this compound decompose into two orbits under action of the symmetry group: 40 of the triangles lie in coplanar pairs in icosahedral planes, while the other 60 lie in unique planes.-...	sne		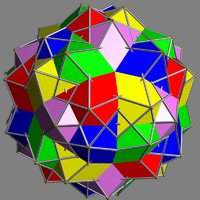5	icosahedra Icosahedron In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids....	(40+60){3}	150	60		Ih Icosahedral symmetry A regular icosahedron has 60 rotational symmetries, and a symmetry order of 120 including transformations that combine a reflection and a rotation...	Th Tetrahedral symmetry 150px|right|thumb|A regular [[tetrahedron]], an example of a solid with full tetrahedral symmetryA regular tetrahedron has 12 rotational symmetries, and a symmetry order of 24 including transformations that combine a reflection and a rotation.The group of all symmetries is isomorphic to the group...
UC48 Compound of two great dodecahedra This uniform polyhedron compound is a composition of 2 great dodecahedra, in the same arrangement as in the compound of 2 icosahedra.- External links :* VRML model:...	presipsido		2	great dodecahedra	24{5}	60	24		Oh Octahedral symmetry 150px|thumb|right|The [[cube]] is the most common shape with octahedral symmetryA regular octahedron has 24 rotational symmetries, and a symmetry order of 48 including transformations that combine a reflection and a rotation...	Th Tetrahedral symmetry 150px|right|thumb|A regular [[tetrahedron]], an example of a solid with full tetrahedral symmetryA regular tetrahedron has 12 rotational symmetries, and a symmetry order of 24 including transformations that combine a reflection and a rotation.The group of all symmetries is isomorphic to the group...
UC49 Compound of five great dodecahedra This uniform polyhedron compound is a composition of 5 great dodecahedra, in the same arrangement as in the compound of 5 icosahedra....	presipsi		5	great dodecahedra	60{5}	150	60		Ih Icosahedral symmetry A regular icosahedron has 60 rotational symmetries, and a symmetry order of 120 including transformations that combine a reflection and a rotation...	Th Tetrahedral symmetry 150px|right|thumb|A regular [[tetrahedron]], an example of a solid with full tetrahedral symmetryA regular tetrahedron has 12 rotational symmetries, and a symmetry order of 24 including transformations that combine a reflection and a rotation.The group of all symmetries is isomorphic to the group...
UC50 Compound of two small stellated dodecahedra This uniform polyhedron compound is a composition of 2 small stellated dodecahedra, in the same arrangement as in the compound of 2 icosahedra.- External links :* VRML model:...	passipsido		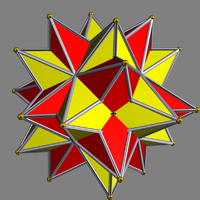2	small stellated dodecahedra	24{5/2}	60	24		Oh Octahedral symmetry 150px|thumb|right|The [[cube]] is the most common shape with octahedral symmetryA regular octahedron has 24 rotational symmetries, and a symmetry order of 48 including transformations that combine a reflection and a rotation...	Th Tetrahedral symmetry 150px|right|thumb|A regular [[tetrahedron]], an example of a solid with full tetrahedral symmetryA regular tetrahedron has 12 rotational symmetries, and a symmetry order of 24 including transformations that combine a reflection and a rotation.The group of all symmetries is isomorphic to the group...
UC51 Compound of five small stellated dodecahedra This uniform polyhedron compound is a composition of 5 small stellated dodecahedra, in the same arrangement as in the compound of 5 icosahedra....	passipsi		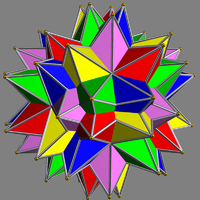5	small stellated dodecahedra	60{5/2}	150	60		Ih Icosahedral symmetry A regular icosahedron has 60 rotational symmetries, and a symmetry order of 120 including transformations that combine a reflection and a rotation...	Th Tetrahedral symmetry 150px|right|thumb|A regular [[tetrahedron]], an example of a solid with full tetrahedral symmetryA regular tetrahedron has 12 rotational symmetries, and a symmetry order of 24 including transformations that combine a reflection and a rotation.The group of all symmetries is isomorphic to the group...
UC52 Compound of two great icosahedra This uniform polyhedron compound is a composition of 2 great icosahedra, in the same arrangement as in the compound of 2 icosahedra.The triangles in this compound decompose into two orbits under action of the symmetry group: 16 of the triangles lie in coplanar pairs in octahedral planes, while the...	sirsido		2	great icosahedra	(16+24){3}	60	24		Oh Octahedral symmetry 150px|thumb|right|The [[cube]] is the most common shape with octahedral symmetryA regular octahedron has 24 rotational symmetries, and a symmetry order of 48 including transformations that combine a reflection and a rotation...	Th Tetrahedral symmetry 150px|right|thumb|A regular [[tetrahedron]], an example of a solid with full tetrahedral symmetryA regular tetrahedron has 12 rotational symmetries, and a symmetry order of 24 including transformations that combine a reflection and a rotation.The group of all symmetries is isomorphic to the group...
UC53 Compound of five great icosahedra This uniform polyhedron compound is a composition of 5 great icosahedra, in the same arrangement as in the compound of 5 icosahedra.The triangles in this compound decompose into two orbits under action of the symmetry group: 40 of the triangles lie in coplanar pairs in icosahedral planes, while the...	sirsei		5	great icosahedra	(40+60){3}	150	60		Ih Icosahedral symmetry A regular icosahedron has 60 rotational symmetries, and a symmetry order of 120 including transformations that combine a reflection and a rotation...	Th Tetrahedral symmetry 150px|right|thumb|A regular [[tetrahedron]], an example of a solid with full tetrahedral symmetryA regular tetrahedron has 12 rotational symmetries, and a symmetry order of 24 including transformations that combine a reflection and a rotation.The group of all symmetries is isomorphic to the group...
UC54 Compound of two truncated tetrahedra This uniform polyhedron compound is a composition of two truncated tetrahedra, formed by truncating each of the tetrahedra in the stella octangula.The vertex arrangement is the same as a convex, but nonuniform rhombicuboctahedron having 12 rectangular faces....	tisso		2	truncated tetrahedra Truncated tetrahedron In geometry, the truncated tetrahedron is an Archimedean solid. It has 4 regular hexagonal faces, 4 regular triangular faces, 12 vertices and 18 edges.- Area and volume :...	8{3} 8{6}	36	24		Oh Octahedral symmetry 150px|thumb|right|The [[cube]] is the most common shape with octahedral symmetryA regular octahedron has 24 rotational symmetries, and a symmetry order of 48 including transformations that combine a reflection and a rotation...	Td Tetrahedral symmetry 150px|right|thumb|A regular [[tetrahedron]], an example of a solid with full tetrahedral symmetryA regular tetrahedron has 12 rotational symmetries, and a symmetry order of 24 including transformations that combine a reflection and a rotation.The group of all symmetries is isomorphic to the group...
UC55 Compound of five truncated tetrahedra This uniform polyhedron compound is a composition of 5 truncated tetrahedra, formed by truncating each of the tetrahedra in the compound of 5 tetrahedra. A far-enough truncation creates the Compound of five octahedra...	taki		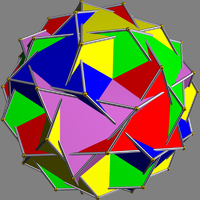5	truncated tetrahedra Truncated tetrahedron In geometry, the truncated tetrahedron is an Archimedean solid. It has 4 regular hexagonal faces, 4 regular triangular faces, 12 vertices and 18 edges.- Area and volume :...	20{3} 20{6}	90	60		I Icosahedral symmetry A regular icosahedron has 60 rotational symmetries, and a symmetry order of 120 including transformations that combine a reflection and a rotation...	T Tetrahedral symmetry 150px|right|thumb|A regular [[tetrahedron]], an example of a solid with full tetrahedral symmetryA regular tetrahedron has 12 rotational symmetries, and a symmetry order of 24 including transformations that combine a reflection and a rotation.The group of all symmetries is isomorphic to the group...
UC56 Compound of ten truncated tetrahedra This uniform polyhedron compound is a composition of 10 truncated tetrahedra, formed by truncating each of the tetrahedra in the compound of 10 tetrahedra. It also results from composing the two enantiomers of the compound of 5 truncated tetrahedra....	te		10	truncated tetrahedra Truncated tetrahedron In geometry, the truncated tetrahedron is an Archimedean solid. It has 4 regular hexagonal faces, 4 regular triangular faces, 12 vertices and 18 edges.- Area and volume :...	40{3} 40{6}	180	120		Ih Icosahedral symmetry A regular icosahedron has 60 rotational symmetries, and a symmetry order of 120 including transformations that combine a reflection and a rotation...	T Tetrahedral symmetry 150px|right|thumb|A regular [[tetrahedron]], an example of a solid with full tetrahedral symmetryA regular tetrahedron has 12 rotational symmetries, and a symmetry order of 24 including transformations that combine a reflection and a rotation.The group of all symmetries is isomorphic to the group...
UC57 Compound of five truncated cubes This uniform polyhedron compound is a composition of 5 truncated cubes, formed by truncating each of the cubes in the compound of 5 cubes.- Cartesian coordinates :Cartesian coordinates for the vertices of this compound are all the cyclic permutations of...	harie		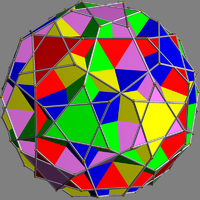5	truncated cube Truncated cube In geometry, the truncated cube, or truncated hexahedron, is an Archimedean solid. It has 14 regular faces , 36 edges, and 24 vertices.... s	40{3} 30{8}	180	120		Ih Icosahedral symmetry A regular icosahedron has 60 rotational symmetries, and a symmetry order of 120 including transformations that combine a reflection and a rotation...	Th Tetrahedral symmetry 150px|right|thumb|A regular [[tetrahedron]], an example of a solid with full tetrahedral symmetryA regular tetrahedron has 12 rotational symmetries, and a symmetry order of 24 including transformations that combine a reflection and a rotation.The group of all symmetries is isomorphic to the group...
UC58 Compound of five stellated truncated cubes This uniform polyhedron compound is a composition of 5 stellated truncated cubes, formed by star-truncating each of the cubes in the compound of 5 cubes.- Cartesian coordinates :...	quahri		5	stellated truncated cubes	40{3} 30{8/3}	180	120		Ih Icosahedral symmetry A regular icosahedron has 60 rotational symmetries, and a symmetry order of 120 including transformations that combine a reflection and a rotation...	Th Tetrahedral symmetry 150px|right|thumb|A regular [[tetrahedron]], an example of a solid with full tetrahedral symmetryA regular tetrahedron has 12 rotational symmetries, and a symmetry order of 24 including transformations that combine a reflection and a rotation.The group of all symmetries is isomorphic to the group...
UC59 Compound of five cuboctahedra In geometry, this uniform polyhedron compound is a composition of 5 cuboctahedra. It has icosahedral symmetry Ih.- Cartesian coordinates :Cartesian coordinates for the vertices of this compound are all the cyclic permutations of...	arie		5	cuboctahedra Cuboctahedron In geometry, a cuboctahedron is a polyhedron with eight triangular faces and six square faces. A cuboctahedron has 12 identical vertices, with two triangles and two squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such it is a quasiregular polyhedron,...	40{3} 30{4}	120	60		Ih Icosahedral symmetry A regular icosahedron has 60 rotational symmetries, and a symmetry order of 120 including transformations that combine a reflection and a rotation...	Th Tetrahedral symmetry 150px|right|thumb|A regular [[tetrahedron]], an example of a solid with full tetrahedral symmetryA regular tetrahedron has 12 rotational symmetries, and a symmetry order of 24 including transformations that combine a reflection and a rotation.The group of all symmetries is isomorphic to the group...
UC60 Compound of five cubohemioctahedra This uniform polyhedron compound is a composition of 5 cubohemioctahedra, in the same arrangement as in the compound of 5 cuboctahedra....	gari		5	cubohemioctahedra Cubohemioctahedron In geometry, the cubohemioctahedron is a nonconvex uniform polyhedron, indexed as U15. Its vertex figure is a crossed quadrilateral.A nonconvex polyhedron has intersecting faces which do not represent new edges or faces...	30{4} 20{6}	120	60		Ih Icosahedral symmetry A regular icosahedron has 60 rotational symmetries, and a symmetry order of 120 including transformations that combine a reflection and a rotation...	Th Tetrahedral symmetry 150px|right|thumb|A regular [[tetrahedron]], an example of a solid with full tetrahedral symmetryA regular tetrahedron has 12 rotational symmetries, and a symmetry order of 24 including transformations that combine a reflection and a rotation.The group of all symmetries is isomorphic to the group...
UC61 Compound of five octahemioctahedra In geometry, this uniform polyhedron compound is a composition of 5 octahemioctahedra, in the same vertex arrangement as in the compound of 5 cuboctahedra....	iddei		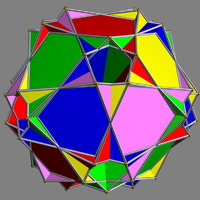5	octahemioctahedra Octahemioctahedron In geometry, the octahemioctahedron is a nonconvex uniform polyhedron, indexed as U3. Its vertex figure is a crossed quadrilateral.It is one of nine hemipolyhedra with 4 hexagonal faces passing through the model center.- Related polyhedra :...	40{3} 20{6}	120	60		Ih Icosahedral symmetry A regular icosahedron has 60 rotational symmetries, and a symmetry order of 120 including transformations that combine a reflection and a rotation...	Th Tetrahedral symmetry 150px|right|thumb|A regular [[tetrahedron]], an example of a solid with full tetrahedral symmetryA regular tetrahedron has 12 rotational symmetries, and a symmetry order of 24 including transformations that combine a reflection and a rotation.The group of all symmetries is isomorphic to the group...
UC62 Compound of five small rhombicuboctahedra This uniform polyhedron compound is a composition of 5 small rhombicuboctahedra, in the same vertex arrangement the compound of 5 stellated truncated cubes....	rasseri		5	small rhombicuboctahedra	40{3} (30+60){4}	240	120		Ih Icosahedral symmetry A regular icosahedron has 60 rotational symmetries, and a symmetry order of 120 including transformations that combine a reflection and a rotation...	Th Tetrahedral symmetry 150px|right|thumb|A regular [[tetrahedron]], an example of a solid with full tetrahedral symmetryA regular tetrahedron has 12 rotational symmetries, and a symmetry order of 24 including transformations that combine a reflection and a rotation.The group of all symmetries is isomorphic to the group...
UC63 Compound of five small rhombihexahedra This uniform polyhedron compound is a composition of 5 small rhombihexahedra, in the same arrangement as the compound of 5 small rhombicuboctahedra....	rasher		5	small rhombihexahedra Small rhombihexahedron In geometry, the small rhombihexahedron is a nonconvex uniform polyhedron, indexed as U18. It has 18 faces , 48 edges, and 24 vertices. Its vertex figure is an antiparallelogram.-Related polyhedra:...	60{4} 30{8}	240	120		Ih Icosahedral symmetry A regular icosahedron has 60 rotational symmetries, and a symmetry order of 120 including transformations that combine a reflection and a rotation...	Th Tetrahedral symmetry 150px|right|thumb|A regular [[tetrahedron]], an example of a solid with full tetrahedral symmetryA regular tetrahedron has 12 rotational symmetries, and a symmetry order of 24 including transformations that combine a reflection and a rotation.The group of all symmetries is isomorphic to the group...
UC64 Compound of five small cubicuboctahedra This uniform polyhedron compound is a composition of 5 small cubicuboctahedra, in the same vertex arrangement as the compound of 5 small rhombicuboctahedra....	rahrie		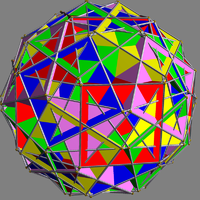5	small cubicuboctahedra Small cubicuboctahedron In geometry, the small cubicuboctahedron is a uniform star polyhedron, indexed as U13. It has 20 faces , 48 edges, and 24 vertices. Its vertex figure is a crossed quadrilateral.- Related polyhedra :...	40{3} 30{4} 30{8}	240	120		Ih Icosahedral symmetry A regular icosahedron has 60 rotational symmetries, and a symmetry order of 120 including transformations that combine a reflection and a rotation...	Th Tetrahedral symmetry 150px|right|thumb|A regular [[tetrahedron]], an example of a solid with full tetrahedral symmetryA regular tetrahedron has 12 rotational symmetries, and a symmetry order of 24 including transformations that combine a reflection and a rotation.The group of all symmetries is isomorphic to the group...
UC65 Compound of five great cubicuboctahedra This uniform polyhedron compound is a composition of 5 great cubicuboctahedra, in the same arrangement as the compound of 5 uniform great rhombicuboctahedra....	raquahri		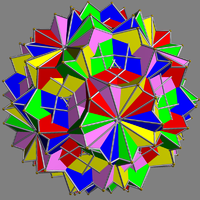5	great cubicuboctahedra Great cubicuboctahedron In geometry, the great cubicuboctahedron is a nonconvex uniform polyhedron, indexed as U14.- Related polyhedra :It shares the vertex arrangement with the convex truncated cube and two other nonconvex uniform polyhedra...	40{3} 30{4} 30{8/3}	240	120		Ih Icosahedral symmetry A regular icosahedron has 60 rotational symmetries, and a symmetry order of 120 including transformations that combine a reflection and a rotation...	Th Tetrahedral symmetry 150px|right|thumb|A regular [[tetrahedron]], an example of a solid with full tetrahedral symmetryA regular tetrahedron has 12 rotational symmetries, and a symmetry order of 24 including transformations that combine a reflection and a rotation.The group of all symmetries is isomorphic to the group...
UC66 Compound of five great rhombihexahedra This uniform polyhedron compound is a composition of 5 great rhombihexahedra, in the same arrangement as the compound of 5 uniform great rhombicuboctahedra....	rasquahr		5	great rhombihexahedra Great rhombihexahedron In geometry, the great rhombihexahedron is a nonconvex uniform polyhedron, indexed as U21. Its dual is the great rhombihexacron. Its vertex figure is a crossed quadrilateral.- Related polyhedra :...	60{4} 30{8/3}	240	120		Ih Icosahedral symmetry A regular icosahedron has 60 rotational symmetries, and a symmetry order of 120 including transformations that combine a reflection and a rotation...	Th Tetrahedral symmetry 150px|right|thumb|A regular [[tetrahedron]], an example of a solid with full tetrahedral symmetryA regular tetrahedron has 12 rotational symmetries, and a symmetry order of 24 including transformations that combine a reflection and a rotation.The group of all symmetries is isomorphic to the group...
UC67 Compound of five uniform great rhombicuboctahedra This uniform polyhedron compound is a composition of 5 uniform great rhombicuboctahedra, in the same arrangement the compound of 5 truncated cubes....	rasquahpri		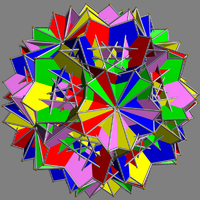5	uniform great rhombicuboctahedra	40{3} (30+60){4}	240	120		Ih Icosahedral symmetry A regular icosahedron has 60 rotational symmetries, and a symmetry order of 120 including transformations that combine a reflection and a rotation...	Th Tetrahedral symmetry 150px|right|thumb|A regular [[tetrahedron]], an example of a solid with full tetrahedral symmetryA regular tetrahedron has 12 rotational symmetries, and a symmetry order of 24 including transformations that combine a reflection and a rotation.The group of all symmetries is isomorphic to the group...
UC68 Compound of two snub cubes This uniform polyhedron compound is a composition of the 2 enantiomers of the snub cube.The vertex arrangement of this compound is shared by a convex nonuniform truncated cuboctahedron, having rectangular faces, alongside irregular hexagons and octagons, each alternating with two edge lengths....	disco		2	snub cube Snub cube In geometry, the snub cube, or snub cuboctahedron, is an Archimedean solid.The snub cube has 38 faces, 6 of which are squares and the other 32 are equilateral triangles. It has 60 edges and 24 vertices. It is a chiral polyhedron, that is, it has two distinct forms, which are mirror images of each... s	(16+48){3} 12{4}	120	48		Oh Octahedral symmetry 150px|thumb|right|The [[cube]] is the most common shape with octahedral symmetryA regular octahedron has 24 rotational symmetries, and a symmetry order of 48 including transformations that combine a reflection and a rotation...	O Octahedral symmetry 150px|thumb|right|The [[cube]] is the most common shape with octahedral symmetryA regular octahedron has 24 rotational symmetries, and a symmetry order of 48 including transformations that combine a reflection and a rotation...
UC69 Compound of two snub dodecahedra This uniform polyhedron compound is a composition of the 2 enantiomers of the snub dodecahedron.The vertex arrangement of this compound is shared by a convex nonuniform truncated icosidodecahedron, with rectangular faces, alongside irregular hexagons and decagons, each alternating two different...	dissid		2	snub dodecahedra Snub dodecahedron In geometry, the snub dodecahedron, or snub icosidodecahedron, is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids constructed by two or more types of regular polygon faces....	(40+120){3} 24{5}	300	120		Ih Icosahedral symmetry A regular icosahedron has 60 rotational symmetries, and a symmetry order of 120 including transformations that combine a reflection and a rotation...	I Icosahedral symmetry A regular icosahedron has 60 rotational symmetries, and a symmetry order of 120 including transformations that combine a reflection and a rotation...
UC70 Compound of two great snub icosidodecahedra This uniform polyhedron compound is a composition of the 2 enantiomers of the great snub icosidodecahedron....	giddasid		2	great snub icosidodecahedra	(40+120){3} 24{5/2}	300	120		Ih Icosahedral symmetry A regular icosahedron has 60 rotational symmetries, and a symmetry order of 120 including transformations that combine a reflection and a rotation...	I Icosahedral symmetry A regular icosahedron has 60 rotational symmetries, and a symmetry order of 120 including transformations that combine a reflection and a rotation...
UC71 Compound of two great inverted snub icosidodecahedra This uniform polyhedron compound is a composition of the 2 enantiomers of the great inverted snub icosidodecahedron....	gidsid		2	great inverted snub icosidodecahedra	(40+120){3} 24{5/2}	300	120		Ih Icosahedral symmetry A regular icosahedron has 60 rotational symmetries, and a symmetry order of 120 including transformations that combine a reflection and a rotation...	I Icosahedral symmetry A regular icosahedron has 60 rotational symmetries, and a symmetry order of 120 including transformations that combine a reflection and a rotation...
UC72 Compound of two great retrosnub icosidodecahedra This uniform polyhedron compound is a composition of the 2 enantiomers of the great retrosnub icosidodecahedron....	gidrissid		2	great retrosnub icosidodecahedra	(40+120){3} 24{5/2}	300	120		Ih Icosahedral symmetry A regular icosahedron has 60 rotational symmetries, and a symmetry order of 120 including transformations that combine a reflection and a rotation...	I Icosahedral symmetry A regular icosahedron has 60 rotational symmetries, and a symmetry order of 120 including transformations that combine a reflection and a rotation...
UC73 Compound of two snub dodecadodecahedra This uniform polyhedron compound is a composition of the 2 enantiomers of the snub dodecadodecahedron....	disdid		2	snub dodecadodecahedra	120{3} 24{5} 24{5/2}	300	120		Ih Icosahedral symmetry A regular icosahedron has 60 rotational symmetries, and a symmetry order of 120 including transformations that combine a reflection and a rotation...	I Icosahedral symmetry A regular icosahedron has 60 rotational symmetries, and a symmetry order of 120 including transformations that combine a reflection and a rotation...
UC74 Compound of two inverted snub dodecadodecahedra This uniform polyhedron compound is a composition of the 2 enantiomers of the inverted snub dodecadodecahedron....	idisdid		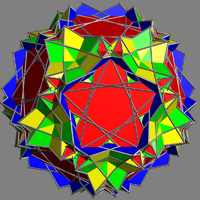2	inverted snub dodecadodecahedra	120{3} 24{5} 24{5/2}	300	120		Ih Icosahedral symmetry A regular icosahedron has 60 rotational symmetries, and a symmetry order of 120 including transformations that combine a reflection and a rotation...	I Icosahedral symmetry A regular icosahedron has 60 rotational symmetries, and a symmetry order of 120 including transformations that combine a reflection and a rotation...
UC75 Compound of two snub icosidodecadodecahedra This uniform polyhedron compound is a composition of the 2 enantiomers of the snub icosidodecadodecahedron....	decided		2	snub icosidodecadodecahedra Snub icosidodecadodecahedron In geometry, the snub icosidodecadodecahedron is a nonconvex uniform polyhedron, indexed as U46.- Cartesian coordinates :Cartesian coordinates for the vertices of a snub icosidodecadodecahedron are all the even permutations of...	(40+120){3} 24{5} 24{5/2}	360	120		Ih Icosahedral symmetry A regular icosahedron has 60 rotational symmetries, and a symmetry order of 120 including transformations that combine a reflection and a rotation...	I Icosahedral symmetry A regular icosahedron has 60 rotational symmetries, and a symmetry order of 120 including transformations that combine a reflection and a rotation...

External links

• http://www.interocitors.com/polyhedra/UCs/ShortNames.html - Bowers style acronyms for uniform polyhedron compounds