Small cubicuboctahedron
Encyclopedia
In geometry
, the small cubicuboctahedron is a uniform star polyhedron, indexed as U13. It has 20 faces (8 triangles, 6 squares, and 6 octagons), 48 edges, and 24 vertices. Its vertex figure
is a crossed quadrilateral.
with the stellated truncated hexahedron. It additionally shares its edge arrangement with the rhombicuboctahedron
(having the triangular faces and 6 square faces in common), and with the small rhombihexahedron
(having the octagonal faces in common).
As the Euler characteristic suggests, the small cubicuboctahedron is a toroidal polyhedron
of genus 3 (topologically it is a surface of genus 3), and thus can be interpreted as a (polyhedral) immersion of a genus 3 polyhedral surface. Stated alternatively, it corresponds to a uniform tiling of this surface. In the language of abstract polytope
s, the small cubicuboctahedron is a faithful realization of this abstract toroidal polyhedron, meaning that it is a nondegenerate polyhedron and that they have the same symmetry group – every automorphism of the abstract genus 3 surface with this tiling is realized by an isometry of Euclidean space (it is a uniform tiling, and the small cubicuboctahedron is a uniform polyhedron).
Higher genus surfaces (genus 2 or greater) admit a metric of negative constant curvature
(by the uniformization theorem
), and the universal cover of the resulting Riemann surface
is the hyperbolic plane. The corresponding tiling of the hyperbolic plane
has vertex figure 3.8.4.8 (triangle, octahedron, square, octahedron) – the covering map is a local isometry and thus the abstract vertex figure is the same (disregarding the factor of ½ which described not how faces are abstractly arranged about a vertex, but how they are concretely realized in Euclidean 3-space). This tiling may be denoted by the (extended) Schläfli symbol t0,1{4, 3, 3}, and is depicted at right.
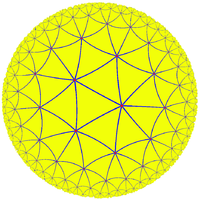Alternatively and more subtly, the small cubicuboctahedron can be interpreted as a coloring of the regular (not just uniform) tiling of the genus 3 surface by 20 equilateral triangles, meeting at 24 vertices, each with degree 7. This regular tiling is significant as it is a tiling of the Klein quartic
, the genus 3 surface with the most symmetric metric (automorphisms of this tiling equal isometries of the surface), and the automorphism group of this surface is isomorphic to the projective special linear group PSL(2,7), equivalently GL(3,2) (order 168, orientation-preserving isometries). Note that the SCCO is not a realization of this abstract polyhedron, as it only have 24 orientation-preserving symmetries (not every abstract automorphism is realized by a Euclidean isometry) – the isometries of the SCCO preserve not only the triangular tiling, but also the coloring, and hence are a proper subgroup of the full isometry group.
The corresponding tiling of the hyperbolic plane (the universal covering) is the order-7 triangular tiling. The automorphism group of the Klein quartic can be augmented (by a symmetry which is not realized by a symmetry of the polyhedron, namely "exchanging the two endpoints of the edges that bisect the squares and octahedrons) to yield the Mathieu group
M24.
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, the small cubicuboctahedron is a uniform star polyhedron, indexed as U13. It has 20 faces (8 triangles, 6 squares, and 6 octagons), 48 edges, and 24 vertices. Its vertex figure
Vertex figure
In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:...
is a crossed quadrilateral.
Related polyhedra
It shares the vertex arrangementVertex arrangement
In geometry, a vertex arrangement is a set of points in space described by their relative positions. They can be described by their use in polytopes....
with the stellated truncated hexahedron. It additionally shares its edge arrangement with the rhombicuboctahedron
Rhombicuboctahedron
In geometry, the rhombicuboctahedron, or small rhombicuboctahedron, is an Archimedean solid with eight triangular and eighteen square faces. There are 24 identical vertices, with one triangle and three squares meeting at each. Note that six of the squares only share vertices with the triangles...
(having the triangular faces and 6 square faces in common), and with the small rhombihexahedron
Small rhombihexahedron
In geometry, the small rhombihexahedron is a nonconvex uniform polyhedron, indexed as U18. It has 18 faces , 48 edges, and 24 vertices. Its vertex figure is an antiparallelogram.-Related polyhedra:...
(having the octagonal faces in common).
 Rhombicuboctahedron Rhombicuboctahedron In geometry, the rhombicuboctahedron, or small rhombicuboctahedron, is an Archimedean solid with eight triangular and eighteen square faces. There are 24 identical vertices, with one triangle and three squares meeting at each. Note that six of the squares only share vertices with the triangles... |
 Small cubicuboctahedron |
 Small rhombihexahedron Small rhombihexahedron In geometry, the small rhombihexahedron is a nonconvex uniform polyhedron, indexed as U18. It has 18 faces , 48 edges, and 24 vertices. Its vertex figure is an antiparallelogram.-Related polyhedra:... |
 Stellated truncated hexahedron |
Related tilings
Toroidal polyhedron
In geometry, a toroidal polyhedron is a polyhedron with a genus of 1 or greater, representing topological torus surfaces.Non-self-intersecting toroidal polyhedra are embedded tori, while self-intersecting toroidal polyhedra are toroidal as abstract polyhedra, which can be verified by their Euler...
of genus 3 (topologically it is a surface of genus 3), and thus can be interpreted as a (polyhedral) immersion of a genus 3 polyhedral surface. Stated alternatively, it corresponds to a uniform tiling of this surface. In the language of abstract polytope
Abstract polytope
In mathematics, an abstract polytope, informally speaking, is a structure which considers only the combinatorial properties of a traditional polytope, ignoring many of its other properties, such as angles, edge lengths, etc...
s, the small cubicuboctahedron is a faithful realization of this abstract toroidal polyhedron, meaning that it is a nondegenerate polyhedron and that they have the same symmetry group – every automorphism of the abstract genus 3 surface with this tiling is realized by an isometry of Euclidean space (it is a uniform tiling, and the small cubicuboctahedron is a uniform polyhedron).
Higher genus surfaces (genus 2 or greater) admit a metric of negative constant curvature
Constant curvature
In mathematics, constant curvature in differential geometry is a concept most commonly applied to surfaces. For those the scalar curvature is a single number determining the local geometry, and its constancy has the obvious meaning that it is the same at all points...
(by the uniformization theorem
Uniformization theorem
In mathematics, the uniformization theorem says that any simply connected Riemann surface is conformally equivalent to one of the three domains: the open unit disk, the complex plane, or the Riemann sphere. In particular it admits a Riemannian metric of constant curvature...
), and the universal cover of the resulting Riemann surface
Riemann surface
In mathematics, particularly in complex analysis, a Riemann surface, first studied by and named after Bernhard Riemann, is a one-dimensional complex manifold. Riemann surfaces can be thought of as "deformed versions" of the complex plane: locally near every point they look like patches of the...
is the hyperbolic plane. The corresponding tiling of the hyperbolic plane
Uniform tilings in hyperbolic plane
There are an infinite number of uniform tilings on the hyperbolic plane based on the where 1/p + 1/q + 1/r ...
has vertex figure 3.8.4.8 (triangle, octahedron, square, octahedron) – the covering map is a local isometry and thus the abstract vertex figure is the same (disregarding the factor of ½ which described not how faces are abstractly arranged about a vertex, but how they are concretely realized in Euclidean 3-space). This tiling may be denoted by the (extended) Schläfli symbol t0,1{4, 3, 3}, and is depicted at right.
Klein quartic
In hyperbolic geometry, the Klein quartic, named after Felix Klein, is a compact Riemann surface of genus 3 with the highest possible order automorphism group for this genus, namely order 168 orientation-preserving automorphisms, and 336 automorphisms if orientation may be reversed...
, the genus 3 surface with the most symmetric metric (automorphisms of this tiling equal isometries of the surface), and the automorphism group of this surface is isomorphic to the projective special linear group PSL(2,7), equivalently GL(3,2) (order 168, orientation-preserving isometries). Note that the SCCO is not a realization of this abstract polyhedron, as it only have 24 orientation-preserving symmetries (not every abstract automorphism is realized by a Euclidean isometry) – the isometries of the SCCO preserve not only the triangular tiling, but also the coloring, and hence are a proper subgroup of the full isometry group.
The corresponding tiling of the hyperbolic plane (the universal covering) is the order-7 triangular tiling. The automorphism group of the Klein quartic can be augmented (by a symmetry which is not realized by a symmetry of the polyhedron, namely "exchanging the two endpoints of the edges that bisect the squares and octahedrons) to yield the Mathieu group
Mathieu group
In the mathematical field of group theory, the Mathieu groups, named after the French mathematician Émile Léonard Mathieu, are five finite simple groups he discovered and reported in papers in 1861 and 1873; these were the first sporadic simple groups discovered...
M24.