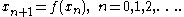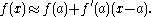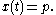Stability theory
Encyclopedia
In mathematics
, stability theory addresses the stability of solutions of differential equation
s and of trajectories of dynamical system
s under small perturbations of initial conditions. The heat equation
, for example, is a stable partial differential equation because small perturbations of initial data lead to small variations in temperature at a later
time as a result of the maximum principle
. More generally, a theorem is stable if small changes in the hypothesis lead to small variations in the conclusion. One must specify
the metric used to measure the perturbations when claiming a theorem is stable.
In partial differential equations one may measure the distances between functions using Lp norms
or the sup norm, while in
differential geometry one may measure the distance between spaces using the Gromov-Hausdorff distance
.
In Dynamical Systems, an orbit
is called Lyapunov stable
if the forward orbit of any point in a small enough neighborhood of it stays in a small (but perhaps, larger) neighborhood. Various criteria have been developed to prove stability or instability of an orbit. Under favorable circumstances, the question may be reduced to a well-studied problem involving eigenvalues of matrices
. A more general method involves Lyapunov function
s.
One of the key ideas in stability theory is that the qualitative behavior of an orbit under perturbations can be analyzed using the linearization
of the system near the orbit. In particular, at each equilibrium of a smooth dynamical system with an n-dimensional phase space
, there is a certain n×n matrix A whose eigenvalues characterize the behavior of the nearby points (Hartman-Grobman theorem
). More precisely, if all eigenvalues are negative real number
s or complex number
s with negative real parts then the point is a stable attracting fixed point, and the nearby points converge to it at an exponential rate, cf Lyapunov stability
and exponential stability. If none of the eigenvalues is purely imaginary (or zero) then the attracting and repelling directions are related to the eigenspaces of the matrix A with eigenvalues whose real part is negative and, respectively, positive. Analogous statements are known for perturbations of more complicated orbits.
s as in the case of a pendulum
. In a system with damping
, a stable equilibrium state is moreover asymptotically stable. On the other hand, for an unstable equilibrium, such as a ball resting on a top of a hill, certain small pushes will result in a motion with a large amplitude that may or may not converge to the original state.
There are useful tests of stability for the case of a linear system. Stability of a nonlinear system can often be inferred from the stability of its linearization
.
The fixed point a is stable if the absolute value
of the derivative
of f at a is strictly less than 1, and unstable if it is strictly greater than 1. This is because near the point a, the function f has a linear approximation
with slope f′(a):
Thus
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, stability theory addresses the stability of solutions of differential equation
Differential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
s and of trajectories of dynamical system
Dynamical system
A dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...
s under small perturbations of initial conditions. The heat equation
Heat equation
The heat equation is an important partial differential equation which describes the distribution of heat in a given region over time...
, for example, is a stable partial differential equation because small perturbations of initial data lead to small variations in temperature at a later
time as a result of the maximum principle
Maximum principle
In mathematics, the maximum principle is a property of solutions to certain partial differential equations, of the elliptic and parabolic types. Roughly speaking, it says that the maximum of a function in a domain is to be found on the boundary of that domain...
. More generally, a theorem is stable if small changes in the hypothesis lead to small variations in the conclusion. One must specify
the metric used to measure the perturbations when claiming a theorem is stable.
In partial differential equations one may measure the distances between functions using Lp norms
Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
or the sup norm, while in
differential geometry one may measure the distance between spaces using the Gromov-Hausdorff distance
Gromov-Hausdorff convergence
In mathematics, Gromov–Hausdorff convergence, named after Mikhail Gromov and Felix Hausdorff, is a notion for convergence of metric spaces which is a generalization of Hausdorff convergence.-Gromov–Hausdorff distance:...
.
In Dynamical Systems, an orbit
Orbit (dynamics)
In mathematics, in the study of dynamical systems, an orbit is a collection of points related by the evolution function of the dynamical system. The orbit is a subset of the phase space and the set of all orbits is a partition of the phase space, that is different orbits do not intersect in the...
is called Lyapunov stable
Lyapunov stability
Various types of stability may be discussed for the solutions of differential equations describing dynamical systems. The most important type is that concerning the stability of solutions near to a point of equilibrium. This may be discussed by the theory of Lyapunov...
if the forward orbit of any point in a small enough neighborhood of it stays in a small (but perhaps, larger) neighborhood. Various criteria have been developed to prove stability or instability of an orbit. Under favorable circumstances, the question may be reduced to a well-studied problem involving eigenvalues of matrices
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
. A more general method involves Lyapunov function
Lyapunov function
In the theory of ordinary differential equations , Lyapunov functions are scalar functions that may be used to prove the stability of an equilibrium of an ODE. Named after the Russian mathematician Aleksandr Mikhailovich Lyapunov, Lyapunov functions are important to stability theory and control...
s.
Overview in Dynamical Systems
Many parts of the qualitative theory of differential equations and dynamical systems deal with asymptotic properties of solutions and the trajectories: what happens with the system after a large time? The simplest kind of behavior is exhibited by equilibrium points, or fixed points, and by periodic orbits. If a particular orbit is well understood, it is natural to ask next whether a small change in the initial condition will lead to similar behavior. Stability theory addresses the following questions: will a nearby orbit indefinitely stay close to a given orbit? will it converge to the given orbit (this is a stronger property)? In the former case, the orbit is called stable and in the latter case, asymptotically stable, or attracting. Stability means that the trajectories do not change too much under small perturbations. The opposite situation, where a nearby orbit is getting repelled from the given orbit, is also of interest. In general, perturbing the initial state in some directions results in the trajectory asymptotically approaching the given one and in other directions to the trajectory getting away from it. There may also be directions for which the behavior of the perturbed orbit is more complicated (neither converging nor escaping completely), and then stability theory does not give sufficient information about the dynamics.One of the key ideas in stability theory is that the qualitative behavior of an orbit under perturbations can be analyzed using the linearization
Linearization
In mathematics and its applications, linearization refers to finding the linear approximation to a function at a given point. In the study of dynamical systems, linearization is a method for assessing the local stability of an equilibrium point of a system of nonlinear differential equations or...
of the system near the orbit. In particular, at each equilibrium of a smooth dynamical system with an n-dimensional phase space
Phase space
In mathematics and physics, a phase space, introduced by Willard Gibbs in 1901, is a space in which all possible states of a system are represented, with each possible state of the system corresponding to one unique point in the phase space...
, there is a certain n×n matrix A whose eigenvalues characterize the behavior of the nearby points (Hartman-Grobman theorem
Hartman-Grobman theorem
In mathematics, in the study of dynamical systems, the Hartman–Grobman theorem or linearization theorem is an important theorem about the local behaviour of dynamical systems in the neighbourhood of a hyperbolic equilibrium point....
). More precisely, if all eigenvalues are negative real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s or complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s with negative real parts then the point is a stable attracting fixed point, and the nearby points converge to it at an exponential rate, cf Lyapunov stability
Lyapunov stability
Various types of stability may be discussed for the solutions of differential equations describing dynamical systems. The most important type is that concerning the stability of solutions near to a point of equilibrium. This may be discussed by the theory of Lyapunov...
and exponential stability. If none of the eigenvalues is purely imaginary (or zero) then the attracting and repelling directions are related to the eigenspaces of the matrix A with eigenvalues whose real part is negative and, respectively, positive. Analogous statements are known for perturbations of more complicated orbits.
Stability of fixed points
The simplest kind of an orbit is a fixed point, or an equilibrium. If a mechanical system is in a stable equilibrium state then a small push will result in a localized motion, for example, small oscillationOscillation
Oscillation is the repetitive variation, typically in time, of some measure about a central value or between two or more different states. Familiar examples include a swinging pendulum and AC power. The term vibration is sometimes used more narrowly to mean a mechanical oscillation but sometimes...
s as in the case of a pendulum
Pendulum
A pendulum is a weight suspended from a pivot so that it can swing freely. When a pendulum is displaced from its resting equilibrium position, it is subject to a restoring force due to gravity that will accelerate it back toward the equilibrium position...
. In a system with damping
Damping
In physics, damping is any effect that tends to reduce the amplitude of oscillations in an oscillatory system, particularly the harmonic oscillator.In mechanics, friction is one such damping effect...
, a stable equilibrium state is moreover asymptotically stable. On the other hand, for an unstable equilibrium, such as a ball resting on a top of a hill, certain small pushes will result in a motion with a large amplitude that may or may not converge to the original state.
There are useful tests of stability for the case of a linear system. Stability of a nonlinear system can often be inferred from the stability of its linearization
Linearization
In mathematics and its applications, linearization refers to finding the linear approximation to a function at a given point. In the study of dynamical systems, linearization is a method for assessing the local stability of an equilibrium point of a system of nonlinear differential equations or...
.
Maps
Let f: R → R be a continuously differentiable function with a fixed point a, f(a) = a. Consider the dynamical system obtained by iterating the function f:The fixed point a is stable if the absolute value
Absolute value
In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
of the derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
of f at a is strictly less than 1, and unstable if it is strictly greater than 1. This is because near the point a, the function f has a linear approximation
Linear approximation
In mathematics, a linear approximation is an approximation of a general function using a linear function . They are widely used in the method of finite differences to produce first order methods for solving or approximating solutions to equations.-Definition:Given a twice continuously...
with slope f′(a):
Thus
-
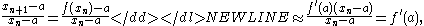
which means that the derivative measures the rate at which the successive iterates approach the fixed point a or diverge from it. If the derivative at a is exactly 1 or −1, then more information is needed in order to decide stability.
There is an analogous criterion for a continuously differentiable map f: Rn → Rn with a fixed point a, expressed in terms of its Jacobian matrix at a, J = Ja(f). If all eigenvalues of J are real or complex numbers with absolute value strictly less than 1 then a is a stable fixed point; if at least one of them has absolute value strictly greater than 1 then a is unstable. Just as for n=1, the case of all eigenvalues having absolute value 1 needs to be investigated further — the Jacobian matrix test is inconclusive. The same criterion holds more generally for diffeomorphismDiffeomorphismIn mathematics, a diffeomorphism is an isomorphism in the category of smooth manifolds. It is an invertible function that maps one differentiable manifold to another, such that both the function and its inverse are smooth.- Definition :...
s of a smooth manifold.
Linear autonomous systems
The stability of fixed points of a system of constant coefficient linear differential equationLinear differential equationLinear differential equations are of the formwhere the differential operator L is a linear operator, y is the unknown function , and the right hand side ƒ is a given function of the same nature as y...
s of first order can be analyzed using the eigenvalues of the corresponding matrix.
An autonomous systemAutonomous system (mathematics)In mathematics, an autonomous system or autonomous differential equation is a system of ordinary differential equations which does not explicitly depend on the independent variable...
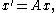
where x(t)∈Rn and A is an n×n matrix with real entries, has a constant solution
(In a different language, the origin 0∈Rn is an equilibrium point of the corresponding dynamical system.) This solution is asymptotically stable as t → ∞ ("in the future") if and only if for all eigenvalues λ of A, Re(λ) < 0. Similarly, it is asymptotically stable as t → −∞ ("in the past") if and only if for all eigenvalues λ of A, Re(λ) > 0. If there exists an eigenvalue λ of A with Re(λ) > 0 then the solution is unstable for t → ∞.
Application of this result in practice, in order to decide the stability of the origin for a linear system, is facilitated by the Routh–Hurwitz stability criterion. The eigenvalues of a matrix are the roots of its characteristic polynomialCharacteristic polynomialIn linear algebra, one associates a polynomial to every square matrix: its characteristic polynomial. This polynomial encodes several important properties of the matrix, most notably its eigenvalues, its determinant and its trace....
. A polynomial in one variable with real coefficients is called a Hurwitz polynomialHurwitz polynomialIn mathematics, a Hurwitz polynomial, named after Adolf Hurwitz, is a polynomial whose coefficients are positive real numbers and whose zeros are located in the left half-plane of the complex plane, that is, the real part of every zero is negative...
if the real parts of all roots are strictly negative. The Routh–Hurwitz theoremRouth–Hurwitz theoremIn mathematics, Routh–Hurwitz theorem gives a test to determine whether a given polynomial is Hurwitz-stable. It was proved in 1895 and named after Edward John Routh and Adolf Hurwitz.-Notations:...
implies a characterization of Hurwitz polynomials by means of an algorithm that avoids computing the roots.
Non-linear autonomous systems
Asymptotic stability of fixed points of a non-linear system can often be established using the Hartman–Grobman theoremHartman-Grobman theoremIn mathematics, in the study of dynamical systems, the Hartman–Grobman theorem or linearization theorem is an important theorem about the local behaviour of dynamical systems in the neighbourhood of a hyperbolic equilibrium point....
.
Suppose that v is a C1-vector fieldVector fieldIn vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
in Rn which vanishes at a point p, v(p)=0. Then the corresponding autonomous system
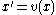
has a constant solution
Let J = Jp(v) be the n×n Jacobian matrix of the vector field v at the point p. If all eigenvalues of J have strictly negative real part then the solution is asymptotically stable. This condition can be tested using the Routh–Hurwitz criterion.
Lyapunov function for general dynamical systems
A general way to establish Lyapunov stabilityLyapunov stabilityVarious types of stability may be discussed for the solutions of differential equations describing dynamical systems. The most important type is that concerning the stability of solutions near to a point of equilibrium. This may be discussed by the theory of Lyapunov...
or asymptotic stability of a dynamical system is by means of Lyapunov functionLyapunov functionIn the theory of ordinary differential equations , Lyapunov functions are scalar functions that may be used to prove the stability of an equilibrium of an ODE. Named after the Russian mathematician Aleksandr Mikhailovich Lyapunov, Lyapunov functions are important to stability theory and control...
s.
See also
- von Neumann stability analysisVon Neumann stability analysisIn numerical analysis, von Neumann stability analysis is a procedure used to check the stability of finite difference schemes as applied to linear partial differential equations...
- Structural stabilityStructural stabilityIn mathematics, structural stability is a fundamental property of a dynamical system which means that the qualitative behavior of the trajectories is unaffected by C1-small perturbations....
- HyperstabilityHyperstabilityIn stability theory, hyperstability is a property of a system that requires the state vector to remain bounded if the inputs are restricted to belonging to a subset of the set of all possible inputs...
- Stability radiusStability radiusThe stability radius of an object at a given nominal point is the radius of the largest ball, centered at the nominal point, all whose elements satisfy pre-determined stability conditions...
External links
- Stable Equilibria by Michael Schreiber, The Wolfram Demonstrations Project.
-