Schur decomposition
Encyclopedia
In the mathematical
discipline of linear algebra
, the Schur decomposition or Schur triangulation, named after Issai Schur
, is a matrix decomposition
.
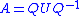
where Q is a unitary matrix (so that its inverse Q−1 is also the conjugate transpose
Q* of Q), and U is an upper triangular matrix, which is called a Schur form of A. Since U is similar to A, it has the same multiset
of eigenvalues, and since it is triangular, those eigenvalues are the diagonal entries of U.
The Schur decomposition implies that there exists a nested sequence of A-invariant subspaces {0} = V0 ⊂ V1 ⊂ ... ⊂ Vn = Cn, and that there exists an ordered orthonormal basis
(for the standard Hermitian form of Cn) such that the first i basis vectors span Vi for each i. Phrased somewhat differently, the first part says that an operator T on a complex finite-dimensional vector space stabilizes a complete flag (V1,...,Vn).
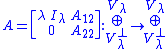
where Iλ is the identity operator on Vλ. The above matrix would be upper-triangular except for the A22 block. But exactly the same procedure can be applied to the sub-matrix A22, viewed as an operator on Vλ⊥, and its submatrices. Continue this way n times. Thus the space Cn will be exhausted and the procedure has yielded the desired result.
The above argument can be slightly restated as follows: let λ be an eigenvalue of A, corresponding to some eigenspace Vλ. A induces an operator T on the quotient space
Cn modulo Vλ. This operator is precisely the A22 submatrix from above. As before, T would have an eigenspace, say Wμ ⊂ Cn modulo Vλ. Notice the preimage of Wμ under the quotient map is an invariant subspace
of A that contains Vλ. Continue this way until the resulting quotient space has dimension 0. Then the successive preimages of the eigenspaces found at each step form a flag that A stabilizes.
applications include:
and 
, where Q and Z are unitary, and S and T are upper triangular. The generalized Schur decomposition is also sometimes called the QZ decomposition.
The generalized eigenvalues
that solve the generalized eigenvalue problem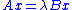 
(where x is an unknown nonzero vector) can be calculated as the ratio of the diagonal elements of S to those of T. That is, using subscripts to denote matrix elements, the ith generalized eigenvalue 
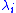satisfies 
.
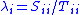Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
discipline of linear algebra
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, the Schur decomposition or Schur triangulation, named after Issai Schur
Issai Schur
Issai Schur was a mathematician who worked in Germany for most of his life. He studied at Berlin...
, is a matrix decomposition
Matrix decomposition
In the mathematical discipline of linear algebra, a matrix decomposition is a factorization of a matrix into some canonical form. There are many different matrix decompositions; each finds use among a particular class of problems.- Example :...
.
Statement
The Schur decomposition reads as follows: if A is a n × n square matrix with complex entries, then A can be expressed as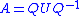where Q is a unitary matrix (so that its inverse Q−1 is also the conjugate transpose
Conjugate transpose
In mathematics, the conjugate transpose, Hermitian transpose, Hermitian conjugate, or adjoint matrix of an m-by-n matrix A with complex entries is the n-by-m matrix A* obtained from A by taking the transpose and then taking the complex conjugate of each entry...
Q* of Q), and U is an upper triangular matrix, which is called a Schur form of A. Since U is similar to A, it has the same multiset
Multiset
In mathematics, the notion of multiset is a generalization of the notion of set in which members are allowed to appear more than once...
of eigenvalues, and since it is triangular, those eigenvalues are the diagonal entries of U.
The Schur decomposition implies that there exists a nested sequence of A-invariant subspaces {0} = V0 ⊂ V1 ⊂ ... ⊂ Vn = Cn, and that there exists an ordered orthonormal basis
Orthonormal basis
In mathematics, particularly linear algebra, an orthonormal basis for inner product space V with finite dimension is a basis for V whose vectors are orthonormal. For example, the standard basis for a Euclidean space Rn is an orthonormal basis, where the relevant inner product is the dot product of...
(for the standard Hermitian form of Cn) such that the first i basis vectors span Vi for each i. Phrased somewhat differently, the first part says that an operator T on a complex finite-dimensional vector space stabilizes a complete flag (V1,...,Vn).
Proof
A constructive proof for the Schur decomposition is as follows: every operator A on a complex finite-dimensional vector space has an eigenvalue λ, corresponding to some eigenspace Vλ. Let Vλ⊥ be its orthogonal complement. It is clear that, with respect to this orthogonal decomposition, A has matrix representation (one can pick here any orthonormal bases spanning Vλ and Vλ⊥ respectively)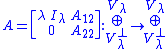where Iλ is the identity operator on Vλ. The above matrix would be upper-triangular except for the A22 block. But exactly the same procedure can be applied to the sub-matrix A22, viewed as an operator on Vλ⊥, and its submatrices. Continue this way n times. Thus the space Cn will be exhausted and the procedure has yielded the desired result.
The above argument can be slightly restated as follows: let λ be an eigenvalue of A, corresponding to some eigenspace Vλ. A induces an operator T on the quotient space
Quotient space (linear algebra)
In linear algebra, the quotient of a vector space V by a subspace N is a vector space obtained by "collapsing" N to zero. The space obtained is called a quotient space and is denoted V/N ....
Cn modulo Vλ. This operator is precisely the A22 submatrix from above. As before, T would have an eigenspace, say Wμ ⊂ Cn modulo Vλ. Notice the preimage of Wμ under the quotient map is an invariant subspace
Invariant subspace
In mathematics, an invariant subspace of a linear mappingfrom some vector space V to itself is a subspace W of V such that T is contained in W...
of A that contains Vλ. Continue this way until the resulting quotient space has dimension 0. Then the successive preimages of the eigenspaces found at each step form a flag that A stabilizes.
Applications
Lie theoryLie theory
Lie theory is an area of mathematics, developed initially by Sophus Lie.Early expressions of Lie theory are found in books composed by Lie with Friedrich Engel and Georg Scheffers from 1888 to 1896....
applications include:
- Every invertible operator is contained in a Borel group.
- Every operator fixes a point of the flag manifoldFlag manifoldIn mathematics, a generalized flag variety is a homogeneous space whose points are flags in a finite-dimensional vector space V over a field F. When F is the real or complex numbers, a generalized flag variety is a smooth or complex manifold, called a real or complex flag manifold...
.
Generalized Schur decomposition
Given square matrices A and B, the generalized Schur decomposition factorizes both matrices as and , where Q and Z are unitary, and S and T are upper triangular. The generalized Schur decomposition is also sometimes called the QZ decomposition.The generalized eigenvalues
that solve the generalized eigenvalue problem 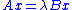(where x is an unknown nonzero vector) can be calculated as the ratio of the diagonal elements of S to those of T. That is, using subscripts to denote matrix elements, the ith generalized eigenvalue 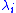satisfies .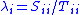