
Small set (combinatorics)
Encyclopedia
In combinatorial
mathematics, a small set of positive integers

is one such that the infinite sum
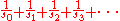
converges
. A large set is any other set of positive integers (i.e. one whose sum diverges
).
Paul Erdős
famously asked the question of whether any set that does not contain arbitrarily long arithmetic progression
s must necessarily be small. He offered a prize of $3000 for the solution to this problem, more than for any of his other conjectures, and joked that this prize offer violated the minimum wage law. This question is still open.
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
mathematics, a small set of positive integers

is one such that the infinite sum
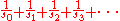
converges
Series (mathematics)
A series is the sum of the terms of a sequence. Finite sequences and series have defined first and last terms, whereas infinite sequences and series continue indefinitely....
. A large set is any other set of positive integers (i.e. one whose sum diverges
Series (mathematics)
A series is the sum of the terms of a sequence. Finite sequences and series have defined first and last terms, whereas infinite sequences and series continue indefinitely....
).
Examples
- The set
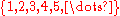 of all positive integers is known to be a large set (see Harmonic seriesHarmonic series (mathematics)In mathematics, the harmonic series is the divergent infinite series:Its name derives from the concept of overtones, or harmonics in music: the wavelengths of the overtones of a vibrating string are 1/2, 1/3, 1/4, etc., of the string's fundamental wavelength...
of all positive integers is known to be a large set (see Harmonic seriesHarmonic series (mathematics)In mathematics, the harmonic series is the divergent infinite series:Its name derives from the concept of overtones, or harmonics in music: the wavelengths of the overtones of a vibrating string are 1/2, 1/3, 1/4, etc., of the string's fundamental wavelength...
), and so is the set obtained from any arithmetic sequence (i.e. of the form an + b with a ≥ 0, b ≥ 1 and n = 0, 1, 2, 3, ...) where a = 0, b = 1 give the multiset and a = 1, b = 1 give
and a = 1, b = 1 give 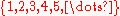 .
.
- The set of square numberSquare numberIn mathematics, a square number, sometimes also called a perfect square, is an integer that is the square of an integer; in other words, it is the product of some integer with itself...
s is small (see Basel problem). So is the set of cube numbers, the set of 4th powers, and so on... And so is the set of any polynomial numbers of degree k ≥ 2 (i.e. of the form , with a ≥ 1, ai ≥ 0 for all i ≥ 1 but ai > 0 for at least one i ≥ 2, and n = 0, 1, 2, 3, ...). Polynomial numbers of degree k < 2 give an arithmetic sequence (which form a large set.) Polynomial numbers of degree 2 give a quadratic sequence which form a small set. Polynomial numbers of degree 3 give a cubic sequence which also form a small set. And so on...
, with a ≥ 1, ai ≥ 0 for all i ≥ 1 but ai > 0 for at least one i ≥ 2, and n = 0, 1, 2, 3, ...). Polynomial numbers of degree k < 2 give an arithmetic sequence (which form a large set.) Polynomial numbers of degree 2 give a quadratic sequence which form a small set. Polynomial numbers of degree 3 give a cubic sequence which also form a small set. And so on...
- The set
 of powers of 2 is known to be a small set, and so is the set of any geometric sequence (i.e. of the form abn with a ≥ 1, b ≥ 2 and n = 0, 1, 2, 3, ...).
of powers of 2 is known to be a small set, and so is the set of any geometric sequence (i.e. of the form abn with a ≥ 1, b ≥ 2 and n = 0, 1, 2, 3, ...).
- The set of prime numberPrime numberA prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
s has been proven to be large. The set of twin primeTwin primeA twin prime is a prime number that differs from another prime number by two. Except for the pair , this is the smallest possible difference between two primes. Some examples of twin prime pairs are , , , , and...
s has been proven to be small (see Brun's constant). A property of prime powersPrime powerIn mathematics, a prime power is a positive integer power of a prime number.For example: 5=51, 9=32 and 16=24 are prime powers, while6=2×3, 15=3×5 and 36=62=22×32 are not...
used frequently in analytic number theoryAnalytic number theoryIn mathematics, analytic number theory is a branch of number theory that uses methods from mathematical analysis to solve problems about the integers. It is often said to have begun with Dirichlet's introduction of Dirichlet L-functions to give the first proof of Dirichlet's theorem on arithmetic...
is that the set of prime powers which are not prime (i.e. all pn with n ≥ 2) is a small set although the primes are a large set.
- The set of perfect powers is small.
- The set of numbers whose decimalDecimalThe decimal numeral system has ten as its base. It is the numerical base most widely used by modern civilizations....
representations exclude 7 (or any digit one prefers) is small. That is, for example, the set
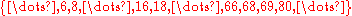
- is small. (This has been generalized to other basesNumeral systemA numeral system is a writing system for expressing numbers, that is a mathematical notation for representing numbers of a given set, using graphemes or symbols in a consistent manner....
as well.) See Kempner series.
Properties
- A unionUnion (set theory)In set theory, the union of a collection of sets is the set of all distinct elements in the collection. The union of a collection of sets S_1, S_2, S_3, \dots , S_n\,\! gives a set S_1 \cup S_2 \cup S_3 \cup \dots \cup S_n.- Definition :...
of finitely many small sets is small, as the sum of two convergent series is a convergent series. A union of infinitely many small sets is either a small set (e.g. the sets of p2, p3, p4, ... where p is prime) or a large set (e.g. the sets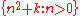 for k > 0). Also, a large set minusComplement (set theory)In set theory, a complement of a set A refers to things not in , A. The relative complement of A with respect to a set B, is the set of elements in B but not in A...
for k > 0). Also, a large set minusComplement (set theory)In set theory, a complement of a set A refers to things not in , A. The relative complement of A with respect to a set B, is the set of elements in B but not in A...
a small set is still large. A large set minus a large set is either a small set (e.g. the set of all prime powers pn with n ≥ 1 minus the set of all primes) or a large set (e.g. the set of all positive integers minus the set of all positive even numbers). In set theoretic terminology, the small sets form an idealIdeal (set theory)In the mathematical field of set theory, an ideal is a collection of sets that are considered to be "small" or "negligible". Every subset of an element of the ideal must also be in the ideal , and the union of any two elements of the ideal must also be in the ideal.More formally, given a set X, an...
.
- The Müntz–Szász theoremMüntz–Szász theoremThe Müntz–Szász theorem is a basic result of approximation theory, proved by Herman Müntz in 1914 and Otto Szász in 1916. Roughly speaking, the theorem shows to what extent the Weierstrass theorem on polynomial approximation can have holes dug into it, by restricting certain coefficients in the...
is that a set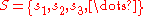 is large if and only if the set spanned by
is large if and only if the set spanned by
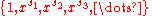
- is denseDense setIn topology and related areas of mathematics, a subset A of a topological space X is called dense if any point x in X belongs to A or is a limit point of A...
in the uniform norm topology of continuous functionContinuous functionIn mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
s on a closed interval. This is a generalization of the Stone–Weierstrass theorem.
Open problems
There are many sets about which it is not known whether they are large or small.Paul Erdős
Paul Erdos
Paul Erdős was a Hungarian mathematician. Erdős published more papers than any other mathematician in history, working with hundreds of collaborators. He worked on problems in combinatorics, graph theory, number theory, classical analysis, approximation theory, set theory, and probability theory...
famously asked the question of whether any set that does not contain arbitrarily long arithmetic progression
Arithmetic progression
In mathematics, an arithmetic progression or arithmetic sequence is a sequence of numbers such that the difference between the consecutive terms is constant...
s must necessarily be small. He offered a prize of $3000 for the solution to this problem, more than for any of his other conjectures, and joked that this prize offer violated the minimum wage law. This question is still open.

