In mathematical analysis

Mathematical analysis

Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...

, the uniform norm

Norm (mathematics)

In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...

assigns to real-

Real number

In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...

 or complex

Complex number

A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...

-valued bounded functions f defined on a set S the nonnegative number


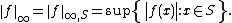
This norm is also called the supremum

Supremum

In mathematics, given a subset S of a totally or partially ordered set T, the supremum of S, if it exists, is the least element of T that is greater than or equal to every element of S. Consequently, the supremum is also referred to as the least upper bound . If the supremum exists, it is unique...

 norm, the Chebyshev norm, or the infinity norm.

If we allow unbounded functions, this formula does not yield a norm or metric

Metric (mathematics)

In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...

 in a strict sense, although the obtained so-called extended metric still allows one to define a topology on the function space in question.

If f is a continuous function

Continuous function

In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...

 on a closed interval, or more generally a compact

Compact space

In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...

 set, then it is bounded and the supremum

Supremum

In mathematics, given a subset S of a totally or partially ordered set T, the supremum of S, if it exists, is the least element of T that is greater than or equal to every element of S. Consequently, the supremum is also referred to as the least upper bound . If the supremum exists, it is unique...

 in the above definition is attained by the Weierstrass extreme value theorem

Extreme value theorem

In calculus, the extreme value theorem states that if a real-valued function f is continuous in the closed and bounded interval [a,b], then f must attain its maximum and minimum value, each at least once...

, so we can replace the supremum by the maximum. In this case, the norm is also called the maximum norm.

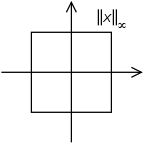
In particular, for the case of a vector 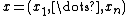in finite dimension

Dimension

In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...

al coordinate space

Coordinate space

In mathematics, specifically in linear algebra, the coordinate space, Fn, is the prototypical example of an n-dimensional vector space over a field F. It can be defined as the product space of F over a finite index set.-Definition:...

, it takes the form


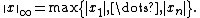
The reason for the subscript "∞" is that whenever f is continuous


where


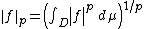
where D is the domain of f (and the integral amounts to a sum if D is a discrete set).

The binary function


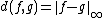
is then a metric

Metric (mathematics)

In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...

 on the space of all bounded functions (and, obviously, any of its subsets) on a particular domain. A sequence { f_n : n = 1, 2, 3, ... } converges uniformly to a function f if and only if


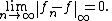
For complex

Complex number

A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...

 continuous functions over a compact space

Compact space

In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...

, this turns it into a C* algebra.

See also

• Chebyshev distance
  Chebyshev distance
  In mathematics, Chebyshev distance , Maximum metric, or L∞ metric is a metric defined on a vector space where the distance between two vectors is the greatest of their differences along any coordinate dimension...
  
  
• Uniform continuity
  Uniform continuity
  In mathematics, a function f is uniformly continuous if, roughly speaking, it is possible to guarantee that f and f be as close to each other as we please by requiring only that x and y are sufficiently close to each other; unlike ordinary continuity, the maximum distance between x and y cannot...
  
  
• Uniform convergence
• Uniform space
  Uniform space
  In the mathematical field of topology, a uniform space is a set with a uniform structure. Uniform spaces are topological spaces with additional structure which is used to define uniform properties such as completeness, uniform continuity and uniform convergence.The conceptual difference between...