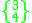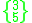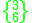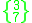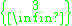
Quasiregular polyhedron
Encyclopedia
|
||||||||||||||||||||||||
|
||||||||||||||||||||||||
In geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, a quasiregular polyhedron is a semiregular polyhedron
Semiregular polyhedron
The term semiregular polyhedron is used variously by different authors.In its original definition, it is a polyhedron with regular faces and a symmetry group which is transitive on its vertices, which is more commonly referred to today as a uniform polyhedron...
that has exactly two kinds of regular faces
Regular polygon
A regular polygon is a polygon that is equiangular and equilateral . Regular polygons may be convex or star.-General properties:...
, which alternate around each vertex. They are edge-transitive and hence step closer to regularity than the semiregular which are merely vertex-transitive
Vertex-transitive
In geometry, a polytope is isogonal or vertex-transitive if, loosely speaking, all its vertices are the same...
.
There are only two convex quasiregular polyhedra, the cuboctahedron
Cuboctahedron
In geometry, a cuboctahedron is a polyhedron with eight triangular faces and six square faces. A cuboctahedron has 12 identical vertices, with two triangles and two squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such it is a quasiregular polyhedron,...
and the icosidodecahedron
Icosidodecahedron
In geometry, an icosidodecahedron is a polyhedron with twenty triangular faces and twelve pentagonal faces. An icosidodecahedron has 30 identical vertices, with two triangles and two pentagons meeting at each, and 60 identical edges, each separating a triangle from a pentagon...
. Their names, given by Kepler, come from recognizing their faces contain all the faces of the dual
Dual polyhedron
In geometry, polyhedra are associated into pairs called duals, where the vertices of one correspond to the faces of the other. The dual of the dual is the original polyhedron. The dual of a polyhedron with equivalent vertices is one with equivalent faces, and of one with equivalent edges is another...
-pair cube
Cube
In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and...
and octahedron
Octahedron
In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....
, in the first, and the dual-pair icosahedron
Icosahedron
In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids....
and dodecahedron in the second case.
These forms representing a pair of a regular figure and its dual can be given a vertical Schläfli symbol
 to represent their containing the faces of both the regular {p,q} and dual regular {q,p}. A quasiregular polyhedron with this symbol will have a vertex configuration
to represent their containing the faces of both the regular {p,q} and dual regular {q,p}. A quasiregular polyhedron with this symbol will have a vertex configurationVertex configuration
In geometry, a vertex configuration is a short-hand notation for representing the vertex figure of a polyhedron or tiling as the sequence of faces around a vertex. For uniform polyhedra there is only one vertex type and therefore the vertex configuration fully defines the polyhedron...
p.q.p.q (or (p.q)2).
More generally, a quasiregular figure can have a vertex configuration
Vertex configuration
In geometry, a vertex configuration is a short-hand notation for representing the vertex figure of a polyhedron or tiling as the sequence of faces around a vertex. For uniform polyhedra there is only one vertex type and therefore the vertex configuration fully defines the polyhedron...
(p.q)r, representing r (2 or more) instances of the faces around the vertex.
Tilings of the plane can also be quasiregular, specifically the trihexagonal tiling
Trihexagonal tiling
In geometry, the trihexagonal tiling is a semiregular tiling of the Euclidean plane. There are two triangles and two hexagons alternating on each vertex...
, with vertex configuration (3.6)2. Other quasiregular tilings
Uniform tilings in hyperbolic plane
There are an infinite number of uniform tilings on the hyperbolic plane based on the where 1/p + 1/q + 1/r ...
exist on the hyperbolic plane, like the triheptagonal tiling
Triheptagonal tiling
In geometry, the triheptagonal tiling is a semiregular tiling of the hyperbolic plane, representing a rectified Order-3 heptagonal tiling. There are two triangles and two heptagons alternating on each vertex...
, (3.7)2. Or more generally, (p.q)2, with 1/p+1/q<1/2.
Some regular polyhedra and tilings (those with an even number of faces at each vertex) can also be considered quasiregular by differentiating between faces of the same number of sides, but representing them differently, like having different colors, but no surface features defining their orientation. A regular figure with Schläfli symbol {p,q} can be quasiregular, with vertex configuration (p.p)q/2, if q is even.
The octahedron
Octahedron
In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....
can be considered quasiregular as a tetratetrahedron (2 sets of 4 triangles of the tetrahedron
Tetrahedron
In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...
), (3a.3b)2, alternating two colors of triangular faces. Similarly the square tiling (4a.4b)2 can be considered quasiregular, colored as a checkerboard. Also the triangular tiling can have alternately colored triangle faces, (3a.3b)3.
Wythoff construction
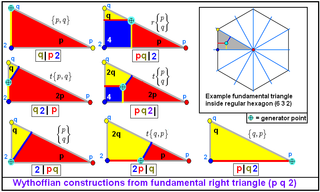
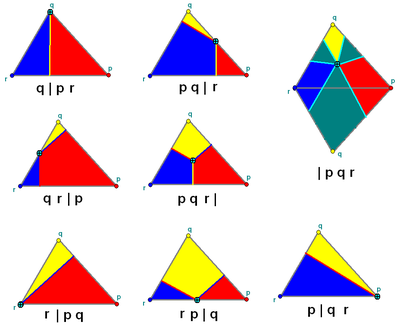
Wythoff symbol
In geometry, the Wythoff symbol was first used by Coxeter, Longeut-Higgens and Miller in their enumeration of the uniform polyhedra. It represents a construction by way of Wythoff's construction applied to Schwarz triangles....
in the form p | q r, and it is regular if q=2 or q=r.
The Coxeter-Dynkin diagram
Coxeter-Dynkin diagram
In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors...
is another symbolic representation that shows the quasiregular relation between the two dual-regular forms:
| Schläfli symbol | Coxeter-Dynkin diagram Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... |
Wythoff symbol Wythoff symbol In geometry, the Wythoff symbol was first used by Coxeter, Longeut-Higgens and Miller in their enumeration of the uniform polyhedra. It represents a construction by way of Wythoff's construction applied to Schwarz triangles.... |
|---|---|---|
 |
q | 2 p | |
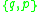 |
p | 2 q | |
 |
2 | p q |
The convex quasiregular polyhedra
There are two convex quasiregular polyhedra:- The cuboctahedronCuboctahedronIn geometry, a cuboctahedron is a polyhedron with eight triangular faces and six square faces. A cuboctahedron has 12 identical vertices, with two triangles and two squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such it is a quasiregular polyhedron,...
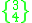 , vertex configuration 3.4.3.4, Coxeter-Dynkin diagramCoxeter-Dynkin diagramIn geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors...
, vertex configuration 3.4.3.4, Coxeter-Dynkin diagramCoxeter-Dynkin diagramIn geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors...
- The icosidodecahedronIcosidodecahedronIn geometry, an icosidodecahedron is a polyhedron with twenty triangular faces and twelve pentagonal faces. An icosidodecahedron has 30 identical vertices, with two triangles and two pentagons meeting at each, and 60 identical edges, each separating a triangle from a pentagon...
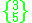 , vertex configuration 3.5.3.5, Coxeter-Dynkin diagram
, vertex configuration 3.5.3.5, Coxeter-Dynkin diagram
In addition, the octahedron
Octahedron
In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....
, which is also regular
Regular polyhedron
A regular polyhedron is a polyhedron whose faces are congruent regular polygons which are assembled in the same way around each vertex. A regular polyhedron is highly symmetrical, being all of edge-transitive, vertex-transitive and face-transitive - i.e. it is transitive on its flags...
,
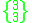 , vertex configuration 3.3.3.3, can be considered quasiregular if alternate faces are given different colors. In this form it is sometimes known as the tetratetrahedron. The remaining convex regular polyhedra have an odd number of faces at each vertex so cannot be colored in a way that preserves edge transitivity. It has Coxeter-Dynkin diagram
, vertex configuration 3.3.3.3, can be considered quasiregular if alternate faces are given different colors. In this form it is sometimes known as the tetratetrahedron. The remaining convex regular polyhedra have an odd number of faces at each vertex so cannot be colored in a way that preserves edge transitivity. It has Coxeter-Dynkin diagram Each of these forms the common core of a dual
Dual polyhedron
In geometry, polyhedra are associated into pairs called duals, where the vertices of one correspond to the faces of the other. The dual of the dual is the original polyhedron. The dual of a polyhedron with equivalent vertices is one with equivalent faces, and of one with equivalent edges is another...
pair of regular polyhedra
Regular polyhedron
A regular polyhedron is a polyhedron whose faces are congruent regular polygons which are assembled in the same way around each vertex. A regular polyhedron is highly symmetrical, being all of edge-transitive, vertex-transitive and face-transitive - i.e. it is transitive on its flags...
. The names of two of these give clues to the associated dual pair, respectively the cube
Cube
In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and...
+ octahedron
Octahedron
In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....
and the icosahedron
Icosahedron
In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids....
+ dodecahedron. The octahedron
Octahedron
In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....
is the core of a dual pair of tetrahedra
Tetrahedron
In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...
(an arrangement known as the stella octangula
Stella octangula
The stellated octahedron, or stella octangula, is the only stellation of the octahedron. It was named by Johannes Kepler in 1609, though it was known to earlier geometers...
), and when derived in this way is sometimes called the tetratetrahedron.
| Regular | Dual regular | Quasiregular | Vertex figure Vertex figure In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:... |
|---|---|---|---|
 3.3.3.3 |
|||
 3.4.3.4 |
|||
 3.5.3.5 |
Each of these quasiregular polyhedra can be constructed by a rectification
Rectification (geometry)
In Euclidean geometry, rectification is the process of truncating a polytope by marking the midpoints of all its edges, and cutting off its vertices at those points...
operation on either regular parent, truncating
Truncation (geometry)
In geometry, a truncation is an operation in any dimension that cuts polytope vertices, creating a new facet in place of each vertex.- Uniform truncation :...
the edges fully, until the original edges are reduced to a point.
Quasiregular tilings
This sequence continues as the trihexagonal tilingTrihexagonal tiling
In geometry, the trihexagonal tiling is a semiregular tiling of the Euclidean plane. There are two triangles and two hexagons alternating on each vertex...
, vertex figure
Vertex figure
In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:...
3.6.3.6 - a quasiregular tiling based on the triangular tiling and hexagonal tiling.
| Regular | Dual regular | Quasiregular | Vertex figure Vertex figure In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:... |
|---|---|---|---|
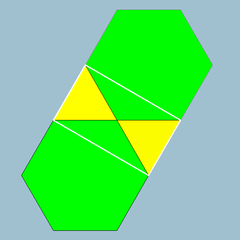 3.6.3.6 |
The checkerboard
Checkerboard
A checkerboard or chequerboard is a board of chequered pattern on which English draughts is played. It is an 8×8 board and the 64 squares are of alternating dark and light color, often red and black....
pattern is a quasiregular coloring of the square tiling, vertex figure
Vertex figure
In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:...
4.4.4.4:
| Regular | Dual regular | Quasiregular | Vertex figure Vertex figure In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:... |
|---|---|---|---|
4.4.4.4 |
The triangular tiling can also be considered quasiregular, with three sets of alternating triangles at each vertex, (3.3)3:
 3 | 3 3 |
In the hyperbolic plane, this sequence continues further, for example the triheptagonal tiling
Triheptagonal tiling
In geometry, the triheptagonal tiling is a semiregular tiling of the hyperbolic plane, representing a rectified Order-3 heptagonal tiling. There are two triangles and two heptagons alternating on each vertex...
, vertex figure
Vertex figure
In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:...
3.7.3.7 - a quasiregular tiling based on the order-7 triangular tiling and heptagonal tiling.
| Regular | Dual regular | Quasiregular | Vertex figure Vertex figure In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:... |
|---|---|---|---|
3.7.3.7 |
Nonconvex examples
Coxeter, H.S.M. et al. (1954) also classify certain star polyhedraStar polyhedron
In geometry, a star polyhedron is a polyhedron which has some repetitive quality of nonconvexity giving it a star-like visual quality.There are two general kinds of star polyhedron:*Polyhedra which self-intersect in a repetitive way....
having the same characteristics as being quasiregular:
Two are based on dual pairs of regular Kepler–Poinsot solids, in the same way as for the convex examples.
The great icosidodecahedron
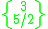 and the dodecadodecahedron
and the dodecadodecahedron 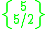 :
:| Regular | Dual regular | Quasiregular | Vertex figure Vertex figure In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:... |
|---|---|---|---|
 great stellated dodecahedron {5/2,3}
|
 great icosahedron {3,5/2}
|
 Great icosidodecahedron 2 | 3 5/2 |
 3.5/2.3.5/2 |
 Small stellated dodecahedron {5/2,5}
|
 Great dodecahedron {5,5/2}
|
 Dodecadodecahedron 2 | 5 5/2 |
 5.5/2.5.5/2 |
Lastly there are three ditrigonal forms, whose vertex figures contain three alternatations of the two face types:
| Polyhedron | Vertex figure Vertex figure In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:... |
|---|---|
 (5.5/3)3 |
|
 (3.5/2)3 |
|
 ((3.5)3)/2 |
Quasiregular duals
Some authorities argue that, since the duals of the quasiregular solids share the same symmetries, these duals must be quasiregular too. But not everybody accepts this view. These duals are transitive on their edges and faces (but not on their vertices); they are the edge-transitive Catalan solidCatalan solid
In mathematics, a Catalan solid, or Archimedean dual, is a dual polyhedron to an Archimedean solid. The Catalan solids are named for the Belgian mathematician, Eugène Catalan, who first described them in 1865....
s. The convex ones are, in corresponding order as above:
- The rhombic dodecahedronRhombic dodecahedronIn geometry, the rhombic dodecahedron is a convex polyhedron with 12 rhombic faces. It is an Archimedean dual solid, or a Catalan solid. Its dual is the cuboctahedron.-Properties:...
, with two types of alternating vertices, 8 with three rhombic faces, and 6 with four rhombic faces. - The rhombic triacontahedronRhombic triacontahedronIn geometry, the rhombic triacontahedron is a convex polyhedron with 30 rhombic faces. It is an Archimedean dual solid, or a Catalan solid. It is the polyhedral dual of the icosidodecahedron, and it is a zonohedron....
, with two types of alternating vertices, 20 with three rhombic faces, and 12 with five rhombic faces.
In addition, by duality with the octahedron, the cube
Cube
In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and...
, which is usually regular
Regular polyhedron
A regular polyhedron is a polyhedron whose faces are congruent regular polygons which are assembled in the same way around each vertex. A regular polyhedron is highly symmetrical, being all of edge-transitive, vertex-transitive and face-transitive - i.e. it is transitive on its flags...
, can be made quasiregular if alternate vertices are given different colors.
Their face configuration
Face configuration
In geometry, a face configuration is notational description of a face-transitive polyhedron. It represents a sequential count of the number of faces that exist at each vertex around a face....
are of the form V3.n.3.n:
 Cube V3.3.3.3 |
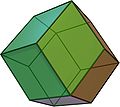 rhombic dodecahedron V3.4.3.4 |
 rhombic triacontahedron V3.5.3.5 |
These three quasiregular duals are also characterised by having rhombic
Rhombus
In Euclidean geometry, a rhombus or rhomb is a convex quadrilateral whose four sides all have the same length. The rhombus is often called a diamond, after the diamonds suit in playing cards, or a lozenge, though the latter sometimes refers specifically to a rhombus with a 45° angle.Every...
faces.
This rhombic-faced pattern continues as V3.6.3.6, the rhombille tiling.
External links
Quasi-regular polyhedra: (p.q)r- George Hart, Quasiregular polyhedra